NNDL 实验五 前馈神经网络(2)自动梯度计算&优化问题
目录
4.3.1 利用预定义算子重新实现前馈神经网络
1,使用pytorch的预定义算子来重新实现二分类任务。
2. 增加一个3个神经元的隐藏层,再次实现二分类,并与1做对比。(必做)
3. 自定义隐藏层层数和每个隐藏层中的神经元个数,尝试找到最优超参数完成二分类。可以适当修改数据集,便于探索超参数。(选做)
4.4.2 梯度消失问题
4.4.3 死亡ReLU问题
![]()
4.3 自动梯度计算
虽然我们能够通过模块化的方式比较好地对神经网络进行组装,但是每个模块的梯度计算过程仍然十分繁琐且容易出错。在深度学习框架中,已经封装了自动梯度计算的功能,我们只需要聚焦模型架构,不再需要耗费精力进行计算梯度。
飞桨提供了paddle.nn.Layer类,来方便快速的实现自己的层和模型。模型和层都可以基于paddle.nn.Layer扩充实现,模型只是一种特殊的层。继承了paddle.nn.Layer类的算子中,可以在内部直接调用其它继承paddle.nn.Layer类的算子,飞桨框架会自动识别算子中内嵌的paddle.nn.Layer类算子,并自动计算它们的梯度,并在优化时更新它们的参数。
pytorch中的相应内容是什么?请简要介绍。
4.3.1 利用预定义算子重新实现前馈神经网络
1,使用pytorch的预定义算子来重新实现二分类任务。
import torch.nn as nn
import torch.nn.functional as F
#from paddle.nn.initializer import Constant, Normal, Uniform
import torch
from torch.nn.parameter import Parameter
class Model_MLP_L2_V2(torch.nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(Model_MLP_L2_V2, self).__init__()
# 使用'paddle.nn.Linear'定义线性层。
# 其中第一个参数(in_features)为线性层输入维度;第二个参数(out_features)为线性层输出维度
# weight_attr为权重参数属性,这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
# bias_attr为偏置参数属性,这里使用'paddle.nn.initializer.Constant'进行常量初始化
self.fc1 = nn.Linear(input_size, hidden_size,)
nn.init.normal_(self.fc1.weight, mean=0, std=1)
nn.init.constant_(self.fc1.bias,0)
self.fc2 = nn.Linear(hidden_size, output_size,)
nn.init.normal_(self.fc2.weight, mean=0, std=1)
nn.init.constant_(self.fc2.bias, 0)
# 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
self.act_fn = torch.sigmoid
# 前向计算
def forward(self, inputs):
z1 = self.fc1(inputs)
a1 = self.act_fn(z1)
z2 = self.fc2(a1)
a2 = self.act_fn(z2)
return a2
class RunnerV2_2(object):
def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
self.model = model
self.optimizer = optimizer
self.loss_fn = loss_fn
self.metric = metric
# 记录训练过程中的评估指标变化情况
self.train_scores = []
self.dev_scores = []
# 记录训练过程中的评价指标变化情况
self.train_loss = []
self.dev_loss = []
def train(self, train_set, dev_set, **kwargs):
# 将模型切换为训练模式
self.model.train()
# 传入训练轮数,如果没有传入值则默认为0
num_epochs = kwargs.get("num_epochs", 0)
# 传入log打印频率,如果没有传入值则默认为100
log_epochs = kwargs.get("log_epochs", 100)
# 传入模型保存路径,如果没有传入值则默认为"best_model.pdparams"
save_path = kwargs.get("save_path", "best_model.pdparams")
# log打印函数,如果没有传入则默认为"None"
custom_print_log = kwargs.get("custom_print_log", None)
# 记录全局最优指标
best_score = 0
# 进行num_epochs轮训练
for epoch in range(num_epochs):
X, y = train_set
# 获取模型预测
logits = self.model(X)
# 计算交叉熵损失
trn_loss = self.loss_fn(logits, y)
self.train_loss.append(trn_loss.item())
# 计算评估指标
trn_score = self.metric(logits, y).item()
self.train_scores.append(trn_score)
# 自动计算参数梯度
trn_loss.backward()
if custom_print_log is not None:
# 打印每一层的梯度
custom_print_log(self)
# 参数更新
self.optimizer.step()
# 清空梯度
self.optimizer.clear_grad()
dev_score, dev_loss = self.evaluate(dev_set)
# 如果当前指标为最优指标,保存该模型
if dev_score > best_score:
self.save_model(save_path)
print(
f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
best_score = dev_score
if log_epochs and epoch % log_epochs == 0:
print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")
# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度
def evaluate(self, data_set):
# 将模型切换为评估模式
self.model.eval()
X, y = data_set
# 计算模型输出
logits = self.model(X)
# 计算损失函数
loss = self.loss_fn(logits, y).item()
self.dev_loss.append(loss)
# 计算评估指标
score = self.metric(logits, y).item()
self.dev_scores.append(score)
return score, loss
# 模型测试阶段,使用'paddle.no_grad()'控制不计算和存储梯度
def predict(self, X):
# 将模型切换为评估模式
self.model.eval()
return self.model(X)
# 使用'model.state_dict()'获取模型参数,并进行保存
def save_model(self, saved_path):
torch.save(self.model.state_dict(), saved_path)
# 使用'model.set_state_dict'加载模型参数
def load_model(self, model_path):
state_dict = torch.load(model_path)
self.model.set_state_dict(state_dict)
4.3.2 完善Runner类
class RunnerV2_2(object):
def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
self.model = model
self.optimizer = optimizer
self.loss_fn = loss_fn
self.metric = metric
# 记录训练过程中的评估指标变化情况
self.train_scores = []
self.dev_scores = []
# 记录训练过程中的评价指标变化情况
self.train_loss = []
self.dev_loss = []
def train(self, train_set, dev_set, **kwargs):
# 将模型切换为训练模式
self.model.train()
# 传入训练轮数,如果没有传入值则默认为0
num_epochs = kwargs.get("num_epochs", 0)
# 传入log打印频率,如果没有传入值则默认为100
log_epochs = kwargs.get("log_epochs", 100)
# 传入模型保存路径,如果没有传入值则默认为"best_model.pdparams"
save_path = kwargs.get("save_path", "best_model.pdparams")
# log打印函数,如果没有传入则默认为"None"
custom_print_log = kwargs.get("custom_print_log", None)
# 记录全局最优指标
best_score = 0
# 进行num_epochs轮训练
for epoch in range(num_epochs):
X, y = train_set
# 获取模型预测
logits = self.model(X)
# 计算交叉熵损失
trn_loss = self.loss_fn(logits, y)
self.train_loss.append(trn_loss.item())
# 计算评估指标
trn_score = self.metric(logits, y).item()
self.train_scores.append(trn_score)
# 清空梯度
optimizer.zero_grad()
# 自动计算参数梯度
trn_loss.backward()
if custom_print_log is not None:
# 打印每一层的梯度
custom_print_log(self)
# 参数更新
self.optimizer.step()
dev_score, dev_loss = self.evaluate(dev_set)
#print(dev_score)
# 如果当前指标为最优指标,保存该模型
if dev_score > best_score:
print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
self.save_model(save_path)
best_score = dev_score
if log_epochs and epoch % log_epochs == 0:
print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")
# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度
def evaluate(self, data_set):
# 将模型切换为评估模式
self.model.eval()
X, y = data_set
# 计算模型输出
logits = self.model(X)
# 计算损失函数
loss = self.loss_fn(logits, y).item()
self.dev_loss.append(loss)
# 计算评估指标
score = self.metric(logits, y).item()
self.dev_scores.append(score)
return score, loss
# 模型测试阶段,使用'paddle.no_grad()'控制不计算和存储梯度
def predict(self, X):
# 将模型切换为评估模式
self.model.eval()
return self.model(X)
# 使用'model.state_dict()'获取模型参数,并进行保存
def save_model(self, saved_path):
torch.save(self.model.state_dict(), saved_path)
# 使用'model.set_state_dict'加载模型参数
def load_model(self, model_path):
state_dict = torch.load(model_path)
self.model.load_state_dict(state_dict)
4.3.3 模型训练
#模型训练
# 设置模型
input_size = 2
hidden_size = 5
output_size = 1
model = Model_MLP_L2_V2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
# 设置损失函数
loss_fn = F.binary_cross_entropy
# 设置优化器
from nndl.opitimizer import Optimizer
learning_rate = 0.2
optimizer = torch. optim.SGD(model.parameters(),learning_rate )
# 设置评价指标
def accuracy(preds, labels):
"""
输入:
- preds:预测值,二分类时,shape=[N, 1],N为样本数量,多分类时,shape=[N, C],C为类别数量
- labels:真实标签,shape=[N, 1]
输出:
- 准确率:shape=[1]
"""
# 判断是二分类任务还是多分类任务,preds.shape[1]=1时为二分类任务,preds.shape[1]>1时为多分类任务
if preds.shape[1] == 1:
# 二分类时,判断每个概率值是否大于0.5,当大于0.5时,类别为1,否则类别为0
# 使用'paddle.cast'将preds的数据类型转换为float32类型
p=[]
for i in range(len(preds)):
#print(preds[i].data)
#print(torch.tensor([1]))
if preds[i]>0.5:
p.append([1])
else:
p.append([0])
p=torch.tensor(p)
return torch.mean(torch.eq(p, labels).float())
else:
# 多分类时,使用'paddle.argmax'计算最大元素索引作为类别
preds = torch.argmax(preds,dim=1).int()
return torch.mean(torch.eq(preds, labels).float())
metric = accuracy
# 其他参数
epoch_num = 1000
saved_path = 'best_model.pdparams'
from nndl.dataset import make_moons
# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.1)
num_train = 640
num_dev = 160
num_test = 200
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]
y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])
# 实例化RunnerV2类,并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_path="best_model.pdparams")
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.53750
[Train] epoch: 0/1000, loss: 0.6784783601760864
[Evaluate] best accuracy performence has been updated: 0.53750 --> 0.62500
[Evaluate] best accuracy performence has been updated: 0.62500 --> 0.70000
[Evaluate] best accuracy performence has been updated: 0.70000 --> 0.71250
[Evaluate] best accuracy performence has been updated: 0.71250 --> 0.72500
[Evaluate] best accuracy performence has been updated: 0.72500 --> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 --> 0.73750
[Evaluate] best accuracy performence has been updated: 0.73750 --> 0.74375
[Evaluate] best accuracy performence has been updated: 0.74375 --> 0.75625
[Evaluate] best accuracy performence has been updated: 0.75625 --> 0.76250
[Evaluate] best accuracy performence has been updated: 0.76250 --> 0.77500
[Evaluate] best accuracy performence has been updated: 0.77500 --> 0.78125
[Evaluate] best accuracy performence has been updated: 0.78125 --> 0.78750
[Train] epoch: 50/1000, loss: 0.45302528142929077
[Evaluate] best accuracy performence has been updated: 0.78750 --> 0.79375
[Evaluate] best accuracy performence has been updated: 0.79375 --> 0.80000
[Evaluate] best accuracy performence has been updated: 0.80000 --> 0.80625
[Evaluate] best accuracy performence has been updated: 0.80625 --> 0.81250
[Evaluate] best accuracy performence has been updated: 0.81250 --> 0.81875
[Train] epoch: 100/1000, loss: 0.4056239724159241
[Evaluate] best accuracy performence has been updated: 0.81875 --> 0.82500
[Evaluate] best accuracy performence has been updated: 0.82500 --> 0.83125
[Evaluate] best accuracy performence has been updated: 0.83125 --> 0.83750
[Train] epoch: 150/1000, loss: 0.37505972385406494
[Train] epoch: 200/1000, loss: 0.35232439637184143
[Evaluate] best accuracy performence has been updated: 0.83750 --> 0.84375
[Evaluate] best accuracy performence has been updated: 0.84375 --> 0.85000
[Evaluate] best accuracy performence has been updated: 0.85000 --> 0.85625
[Train] epoch: 250/1000, loss: 0.3344670832157135
[Evaluate] best accuracy performence has been updated: 0.85625 --> 0.86250
[Evaluate] best accuracy performence has been updated: 0.86250 --> 0.86875
[Evaluate] best accuracy performence has been updated: 0.86875 --> 0.87500
[Evaluate] best accuracy performence has been updated: 0.87500 --> 0.88750
[Train] epoch: 300/1000, loss: 0.32032662630081177
[Train] epoch: 350/1000, loss: 0.3092040717601776
[Train] epoch: 400/1000, loss: 0.3005256950855255
[Train] epoch: 450/1000, loss: 0.29379481077194214
[Evaluate] best accuracy performence has been updated: 0.88750 --> 0.89375
[Train] epoch: 500/1000, loss: 0.2885972857475281
[Train] epoch: 550/1000, loss: 0.2846001982688904
[Train] epoch: 600/1000, loss: 0.2815399169921875
[Train] epoch: 650/1000, loss: 0.2792074382305145
[Train] epoch: 700/1000, loss: 0.2774360179901123
[Train] epoch: 750/1000, loss: 0.276093065738678
[Evaluate] best accuracy performence has been updated: 0.89375 --> 0.90000
[Train] epoch: 800/1000, loss: 0.275073766708374
[Train] epoch: 850/1000, loss: 0.27429693937301636
[Train] epoch: 900/1000, loss: 0.27370065450668335
[Train] epoch: 950/1000, loss: 0.27323827147483826import matplotlib.pyplot as plt
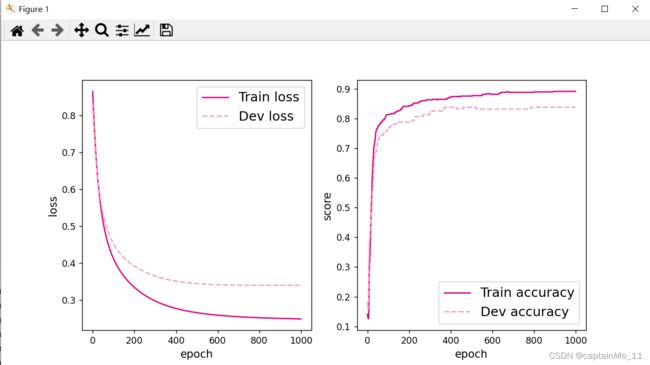
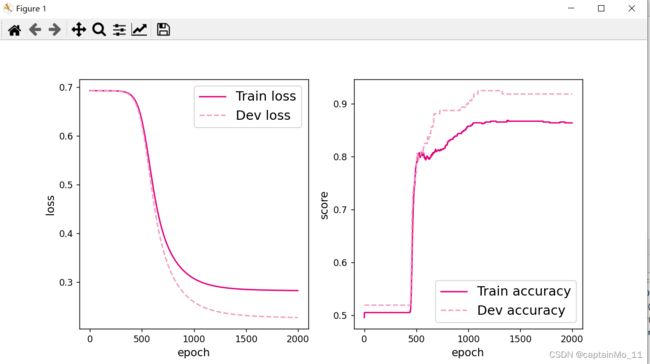
# 可视化观察训练集与验证集的指标变化情况
def plot(runner, fig_name):
plt.figure(figsize=(10, 5))
epochs = [i for i in range(len(runner.train_scores))]
plt.subplot(1, 2, 1)
plt.plot(epochs, runner.train_loss, color='#e4007f', label="Train loss")
plt.plot(epochs, runner.dev_loss, color='#f19ec2', linestyle='--', label="Dev loss")
# 绘制坐标轴和图例
plt.ylabel("loss", fontsize='large')
plt.xlabel("epoch", fontsize='large')
plt.legend(loc='upper right', fontsize='x-large')
plt.subplot(1, 2, 2)
plt.plot(epochs, runner.train_scores, color='#e4007f', label="Train accuracy")
plt.plot(epochs, runner.dev_scores, color='#f19ec2', linestyle='--', label="Dev accuracy")
# 绘制坐标轴和图例
plt.ylabel("score", fontsize='large')
plt.xlabel("epoch", fontsize='large')
plt.legend(loc='lower right', fontsize='x-large')
plt.savefig(fig_name)
plt.show()
plot(runner, 'fw-acc.pdf')
4.3.4 性能评价
# 模型评价
runner.load_model("best_model.pdparams")
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))[Test] score/loss: 0.8250/0.30552. 增加一个3个神经元的隐藏层,再次实现二分类,并与1做对比。(必做)
class Model_MLP_L2_V2(torch.nn.Module):
def __init__(self, input_size, hidden_size,hidden_size2, output_size):
super(Model_MLP_L2_V2, self).__init__()
# 使用'paddle.nn.Linear'定义线性层。
# 其中第一个参数(in_features)为线性层输入维度;第二个参数(out_features)为线性层输出维度
# weight_attr为权重参数属性,这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
# bias_attr为偏置参数属性,这里使用'paddle.nn.initializer.Constant'进行常量初始化
self.fc1 = nn.Linear(input_size, hidden_size,)
nn.init.normal_(self.fc1.weight, mean=0, std=1)
nn.init.constant_(self.fc1.bias,0)
self.fc3=nn.Linear(hidden_size,hidden_size2)
nn.init.normal_(self.fc3.weight, mean=0, std=1)
nn.init.constant_(self.fc3.bias, 0)
self.fc2 = nn.Linear(hidden_size2, output_size,)
nn.init.normal_(self.fc2.weight, mean=0, std=1)
nn.init.constant_(self.fc2.bias, 0)
# 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
self.act_fn = torch.sigmoid
# 前向计算
def forward(self, inputs):
z1 = self.fc1(inputs)
a1 = self.act_fn(z1)
z3= self.fc3(a1)
a3=self.act_fn(z3)
z2 = self.fc2(a3)
a2 = self.act_fn(z2)
return a2[Test] score/loss: 0.8600/0.4793添加一个有4个神经元的隐层后,精确度和损失都有优化。
3. 自定义隐藏层层数和每个隐藏层中的神经元个数,尝试找到最优超参数完成二分类。可以适当修改数据集,便于探索超参数。(选做)
[Test] score/loss: 0.9200/0.2429两层隐层,节点数分别为5,6
[Test] score/loss: 0.9250/0.2431三层隐层,节点数位5,6,10,效果略好于两层隐层。
【思考题】对比自定义梯度计算和自动梯度计算的计算性能、计算结果,谈谈自己的看法。
自动梯度计算有很多优势。首先易于实现,出错率低。在计算性能上,自动梯度计算更快,在结果上自动梯度计算也更精确,不容易出错。如果遇到复杂的神经网络,自动梯度计算的优势更大,它可以用简洁的代码实现,如果用自定义梯度计算,实现起来就要复杂得多。
4.4 优化问题
4.4.1 参数初始化
实现一个神经网络前,需要先初始化模型参数。
class Model_MLP_L2_V4(torch.nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(Model_MLP_L2_V4, self).__init__()
# 使用'paddle.nn.Linear'定义线性层。
# 其中in_features为线性层输入维度;out_features为线性层输出维度
# weight_attr为权重参数属性
# bias_attr为偏置参数属性
self.fc1 = nn.Linear(input_size, hidden_size,)
self.fc2 = nn.Linear(hidden_size, output_size,)
torch.nn.init.constant_(self.fc1.weight,0)
torch.nn.init.constant_(self.fc2.weight, 0)
torch.nn.init.constant_(self.fc1.bias, 0)
torch.nn.init.constant_(self.fc2.bias, 0)
# 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
self.act_fn = torch.sigmoid
# 前向计算
def forward(self, inputs):
z1 = self.fc1(inputs)
a1 = self.act_fn(z1)
z2 = self.fc2(a1)
a2 = self.act_fn(z2)
return a2def print_weights(runner):
print('The weights of the Layers:')
for item in runner.model.state_dict():
print(item)
print(model.state_dict()[item])The weights of the Layers:
fc1.weight
tensor([[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.]])
fc1.bias
tensor([0., 0., 0., 0., 0.])
fc2.weight
tensor([[0., 0., 0., 0., 0.]])
fc2.bias
tensor([0.])
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.49375
[Train] epoch: 0/2000, loss: 0.6931473016738892如果对每一层的权重和偏置都用0初始化,那么通过第一遍前向计算,所有隐藏层神经元的激活值都相同;在反向传播时,所有权重的更新也都相同,这样会导致隐藏层神经元没有差异性,出现对称权重现象。
4.4.2 梯度消失问题
在神经网络的构建过程中,随着网络层数的增加,理论上网络的拟合能力也应该是越来越好的。但是随着网络变深,参数学习更加困难,容易出现梯度消失问题。
由于Sigmoid型函数的饱和性,饱和区的导数更接近于0,误差经过每一层传递都会不断衰减。当网络层数很深时,梯度就会不停衰减,甚至消失,使得整个网络很难训练,这就是所谓的梯度消失问题。
在深度神经网络中,减轻梯度消失问题的方法有很多种,一种简单有效的方式就是使用导数比较大的激活函数,如:ReLU。
from nndl.dataset import make_moons
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.1)
num_train = 640
num_dev = 160
num_test = 200
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]
y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])
torch.seed()
# 学习率大小
lr = 0.01
# 定义网络,激活函数使用sigmoid
model = Model_MLP_L5(input_size=2, output_size=1, act='sigmoid')
# 定义优化器
optimizer = torch. optim.SGD(model.parameters(),lr )
# 定义损失函数,使用交叉熵损失函数
loss_fn = F.binary_cross_entropy
# 定义评价指标
metric = accuracy
# 指定梯度打印函数
custom_print_log=print_grads
# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev],
num_epochs=1, log_epochs=None,
save_path="best_model.pdparams",
custom_print_log=custom_print_log)class Model_MLP_L5(torch.nn.Module):
def __init__(self, input_size, output_size, act='sigmoid',
w_init=torch.nn.init.normal_(torch.rand(3,3),mean=0,std=0.01),
b_init=torch.nn.init.constant_(torch.rand(3,3),val=1.0)):
super(Model_MLP_L5, self).__init__()
self.fc1 = torch.nn.Linear(input_size, 3)
self.fc2 = torch.nn.Linear(3, 3)
self.fc3 = torch.nn.Linear(3, 3)
self.fc4 = torch.nn.Linear(3, 3)
self.fc5 = torch.nn.Linear(3, output_size)
# 定义网络使用的激活函数
if act == 'sigmoid':
self.act = torch.sigmoid
elif act == 'relu':
self.act = torch.relu
elif act == 'lrelu':
self.act = F.leaky_relu
else:
raise ValueError("Please enter sigmoid relu or lrelu!")
# 初始化线性层权重和偏置参数
self.init_weights(w_init, b_init)
# 初始化线性层权重和偏置参数
def init_weights(self, w_init, b_init):
# 使用'named_sublayers'遍历所有网络层
for n, m in enumerate(self.modules()):
# 如果是线性层,则使用指定方式进行参数初始化
if isinstance(m, nn.Linear):
torch.nn.init.normal_(w_init,mean=0,std=0.01)
torch.nn.init.constant_(b_init,val=1.0)
def forward(self, inputs):
outputs = self.fc1(inputs)
outputs = self.act(outputs)
outputs = self.fc2(outputs)
outputs = self.act(outputs)
outputs = self.fc3(outputs)
outputs = self.act(outputs)
outputs = self.fc4(outputs)
outputs = self.act(outputs)
outputs = self.fc5(outputs)
outputs = torch.sigmoid(outputs)
return outputsdef print_grads(runner):
# 打印每一层的权重的模
print('The gradient of the Layers:')
for item in runner.model.named_parameters():
if len(item[1])==3:
print(item[0],".gard:")
print(torch.mean(item[1].grad))
print("=============")The gradient of the Layers:
fc1.weight .gard:
tensor(1.6457e-06)
=============
fc1.bias .gard:
tensor(2.0551e-06)
=============
fc2.weight .gard:
tensor(1.6275e-05)
=============
fc2.bias .gard:
tensor(3.2316e-05)
=============
fc3.weight .gard:
tensor(5.5536e-05)
=============
fc3.bias .gard:
tensor(9.8989e-05)
=============
fc4.weight .gard:
tensor(-0.0003)
=============
fc4.bias .gard:
tensor(-0.0006)
=============
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.46875
Process finished with exit code 0
使用lregu激活函数后:
The gradient of the Layers:
fc1.weight .gard:
tensor(-3.8817e-06)
=============
fc1.bias .gard:
tensor(-1.2626e-05)
=============
fc2.weight .gard:
tensor(2.3137e-05)
=============
fc2.bias .gard:
tensor(5.6947e-05)
=============
fc3.weight .gard:
tensor(-6.8904e-08)
=============
fc3.bias .gard:
tensor(-0.0001)
=============
fc4.weight .gard:
tensor(-2.3767e-06)
=============
fc4.bias .gard:
tensor(-6.4036e-06)
=============
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.468754.4.3 死亡ReLU问题
ReLU激活函数可以一定程度上改善梯度消失问题,但是ReLU函数在某些情况下容易出现死亡 ReLU问题,使得网络难以训练。
这是由于当x<0x<0时,ReLU函数的输出恒为0。在训练过程中,如果参数在一次不恰当的更新后,某个ReLU神经元在所有训练数据上都不能被激活(即输出为0),那么这个神经元自身参数的梯度永远都会是0,在以后的训练过程中永远都不能被激活。
一种简单有效的优化方式就是将激活函数更换为Leaky ReLU、ELU等ReLU的变种。
The gradient of the Layers:
fc1.weight .gard:
tensor(0.)
=============
fc1.bias .gard:
tensor(0.)
=============
fc2.weight .gard:
tensor(0.)
=============
fc2.bias .gard:
tensor(0.)
=============
fc3.weight .gard:
tensor(0.)
=============
fc3.bias .gard:
tensor(0.0014)
=============
fc4.weight .gard:
tensor(-0.0016)
=============
fc4.bias .gard:
tensor(-0.0194)
=============
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.46875一些梯度为0 ,出现了死亡relu现象
使用lregu激活函数后
The gradient of the Layers:
fc1.weight .gard:
tensor(4.0675e-05)
=============
fc1.bias .gard:
tensor(6.5517e-05)
=============
fc2.weight .gard:
tensor(6.5789e-06)
=============
fc2.bias .gard:
tensor(1.5382e-06)
=============
fc3.weight .gard:
tensor(-8.0225e-05)
=============
fc3.bias .gard:
tensor(-6.3153e-06)
=============
fc4.weight .gard:
tensor(4.2280e-05)
=============
fc4.bias .gard:
tensor(-0.0008)
=============
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.45000
使用lrelu后,梯度全不为0,没有出现死亡relu问题。
总结:
这次实验掌握了自动梯度计算的方法,了解到了自动梯度计算的优势。以及激活函数的优化问题,权值的初始化选择。解决梯度消失,regu死亡的方法。