深度学习教程(4) | 深层神经网络（吴恩达·完整版）

• 作者：韩信子@ShowMeAI
• 教程地址：https://www.showmeai.tech/tutorials/35
• 本文地址：https://www.showmeai.tech/article-detail/215
• 声明：版权所有，转载请联系平台与作者并注明出处
• 收藏ShowMeAI查看更多精彩内容

---

本系列为吴恩达老师《深度学习专项课程(Deep Learning Specialization)》学习与总结整理所得，对应的课程视频可以在这里查看。

引言

在ShowMeAI前一篇文章 浅层神经网络 中我们对以下内容进行了介绍:

• 神经网络的基本结构(输入层，隐藏层和输出层)。
• 浅层神经网络前向传播和反向传播过程。
• 神经网络参数的梯度下降优化。
• 不同的激活函数的优缺点及非线性的原因。
• 神经网络参数随机初始化方式

本篇内容我们将讨论深层神经网络。

1.深层神经网络

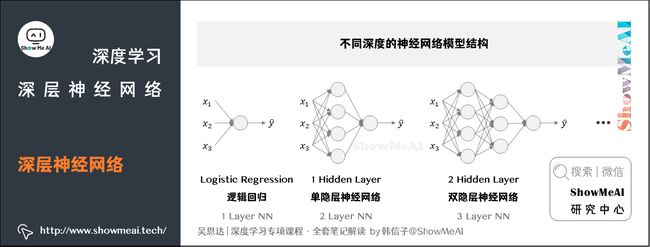
我们在前面提到了浅层神经网络，深层神经网络其实就是包含更多隐层的神经网络。下图分别列举了不同深度的神经网络模型结构：

我们会参考「隐层个数」和「输出层」对齐命名。如上图逻辑回归可以叫做1 layer NN，单隐层神经网络可以叫做2 layer NN，2个隐层的神经网络叫做3 layer NN，以此类推。所以当我们提到L layer NN，指的是包含$L-1$个隐层的神经网络。

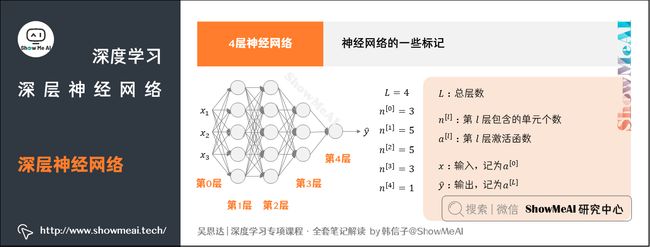
下面我们来了解一下神经网络的一些标记写法。以如下图的4层神经网络为例：

① 总层数用$L$表示，$L=4$

• 输入层是第$0$层，输出层是第$L$层

② $n^{[l]}$表示第$l$层包含的单元个数，$l=0,1,\cdots ,L$

• 下图模型中，$n^{[0]}=n_x=3$，表示三个输入特征$x_1$、$x_2$、$x_3$

• 下图模型中$n^{[1]}=5$，$n^{[2]}=5$，$n^{[3]}=3$，$n^{[4]}=n^{[L]}=1$

③ 第$l$层的激活函数输出用$a^{[l]}$表示，$a^{[l]}=g^{[l]}(z^{[l]})$

④ $W^{[l]}$表示第$l$层的权重，用于计算$z^{[l]}$

⑤ 输入$x$记为$a^{[0]}$

⑥ 输出层$\hat{y}$记为$a^{[L]}$

注意，$a^{[l]}$和$W^{[l]}$中的上标$l$都是从1开始的，$l=1,\cdots ,L$。

2.深层神经网络前向运算

下面我们来推导一下深层神经网络的前向传播计算过程。依旧是上面提到的4层神经网络，我们以其为例来做讲解。

2.1 单个样本的计算

对于单个样本，我们有：

2.2 m个样本的批量计算

对于$m$个训练样本的情况，我们以向量化矩阵形式来并行计算：

以此类推，对于第$l$层，其前向传播过程的$Z^{[l]}$和$A^{[l]}$可以表示为：

$$Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}$$

$$A^{[l]}=g^{[l]}(Z^{[l]})$$

其中$l=1,\cdots ,L$

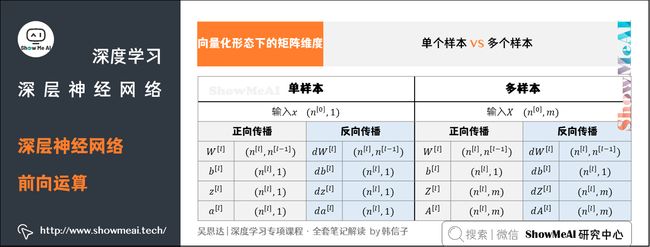
3.向量化形态下的矩阵维度

在单个训练样本的场景下，输入$x$的维度是$(n^{[0]},1)$神经网络的参数$W^{[l]}$和$b^{[l]}$的维度分别是：

• $W^{[l]}:(n^{[l]},n^{[l-1]})$

• $b^{[l]}:(n^{[l]},1)$

其中，

• $l=1,\cdots ,L$
• $n^{[l]}$和$n^{[l-1]}$分别表示第$l$层和$l-1$层的所含单元个数
• $n^{[0]}=n_x$，表示输入层特征数目

对应的反向传播过程中的$d{W}^{[l]}$和$d{b}^{[l]}$的维度分别是：

• $d{W}^{[l]}:(n^{[l]},n^{[l-1]})$

• $d{b}^{[l]}:(n^{[l]},1)$

• 注意到，$W^{[l]}$与$d{W}^{[l]}$维度相同，$b^{[l]}$与$d{b}^{[l]}$维度相同。这很容易理解。

正向传播过程中的$z^{[l]}$和$a^{[l]}$的维度分别是：

• $z^{[l]}:(n^{[l]},1)$

• $a^{[l]}:(n^{[l]},1)$

• $z^{[l]}$和$a^{[l]}$的维度是一样的，且$d{z}^{[l]}$和$d{a}^{[l]}$的维度均与$z^{[l]}$和$a^{[l]}$的维度一致。

对于$m$个训练样本，输入矩阵$X$的维度是$(n^{[0]},m)$。需要注意的是$W^{[l]}$和$b^{[l]}$的维度与只有单个样本是一致的：

• $W^{[l]}:(n^{[l]},n^{[l-1]})$

• $b^{[l]}:(n^{[l]},1)$

只不过在运算$Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}$中，$b^{[l]}$会被当成$(n^{[l]},m)$矩阵进行运算，这是基于python numpy的广播特性，且$b^{[l]}$每一列向量都是一样的。$d{W}^{[l]}$和$d{b}^{[l]}$的维度分别与$W^{[l]}$和$b^{[l]}$的相同。

不过，$Z^{[l]}$和$A^{[l]}$的维度发生了变化：

• $Z^{[l]}:(n^{[l]},m)$

• $A^{[l]}:(n^{[l]},m)$

• $d{Z}^{[l]}$和$d{A}^{[l]}$的维度分别与$Z^{[l]}$和$A^{[l]}$的相同。

4.为什么需要深度网络

当今大家看到的很多AI智能场景背后都是巨大的神经网络在支撑，强大能力很大一部分来源于神经网络足够“深”，也就是说随着网络层数增多，神经网络就更加复杂参数更多，学习能力也更强。下面是一些典型的场景例子说明。

4.1 人脸识别例子

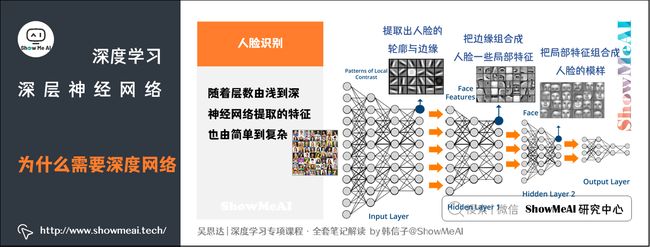
如下图所示的人脸识别场景，训练得到的神经网络，每一层的作用有差别：

• 第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘，即边缘检测。这样每个神经元得到的是一些边缘信息。
• 第二层所做的事情就是将前一层的边缘进行组合，组合成人脸一些局部特征，比如眼睛、鼻子、嘴巴等。
• 后续层次逐层把这些局部特征组合起来，融合成人脸的模样。

可以看出，随着层数由浅到深，神经网络提取的特征也是从边缘到局部特征到整体，由简单到复杂。隐藏层越多，能够提取的特征就越丰富、越复杂，模型的准确率也可能会随之越高。（详细的人脸识别原理可以查看ShowMeAI的文章 CNN应用：人脸识别和神经风格转换 ）

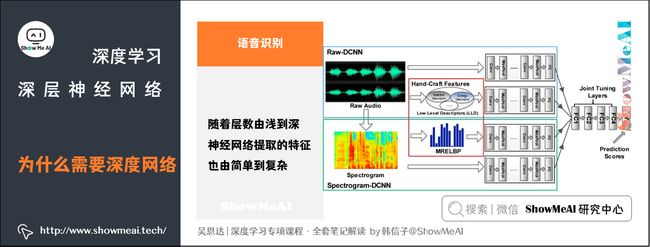
4.2 语音识别例子

语音识别模型也是类似的道理：

• 浅层的神经元能够检测一些简单的音调
• 较深的神经元能够检测出基本的音素
• 更深的神经元就能够检测出单词信息
• 网络足够深的话，还能对短语、句子进行检测

神经网络从浅到深，提取的特征从简单到复杂。特征复杂度与神经网络层数成正相关。特征越来越复杂，表达能力和功能也越强。（详细的语音识别原理知识可以查看ShowMeAI的文章 Seq2seq序列模型和注意力机制 ）

4.3 深度网络其他优势

除学习能力与特征提取强度之外，深层网络还有另外一个优点，就是能够减少神经元个数，从而减少计算量。

下面有一个例子，使用电路理论，计算逻辑输出：

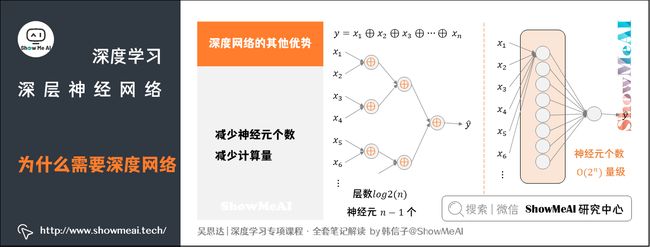
$$y=x_1\oplus x_2\oplus x_3\oplus \cdots \oplus x_n$$

• 上面的计算表达式中，$\oplus$表示「异或」操作。

对于这个逻辑运算，如果使用深度网络完成，每层将前一层的两两单元进行异或，最后到一个输出，如下图左边所示。

这样，整个深度网络的层数是$lo{g}_2(n)$(不包含输入层)。总共使用的神经元个数为：

$$1+2+\cdots +2^{lo{g}_2(n)-1}=1\cdot \frac{1-2^{lo{g}_2(n)}}{1-2}=2^{lo{g}_2(n)}-1=n-1$$

可见，输入个数是$n$，这种深层网络所需的神经元个数仅仅是$n-1$个。

如果不用深层网络，仅仅使用单个隐藏层，如上右图所示，由于包含了所有的逻辑位(0和1)，那么需要的神经元个数$O(2^n)$是指数级别的大小。

对于其他场景和问题也一样，处理同样的逻辑问题，深层网络所需的神经元个数比浅层网络要少很多。这也是深层神经网络的优点之一。

尽管深度学习有着非常显著的优势，吴恩达老师还是建议对实际问题进行建模时，尽量先选择层数少的神经网络模型，这也符合奥卡姆剃刀定律(Occam’s Razor)。对于比较复杂的问题，再使用较深的神经网络模型。

5.构建深度网络单元块

下面用流程块图来解释神经网络前向传播和反向传播过程。

如图所示，对于第$l$层来说，前向传播过程中，我们有：

• 输入：$a^{[l-1]} $
• 输出：$a^{[l]} $
• 参数：$W^{[l]}$、$b^{[l]}$
• 缓存变量：$z^{[l]} $

反向传播过程中：

• 输入：$da^{[l]} $
• 输出：$da^{[l-1]} $、$dW^{[l]} $、$db^{[l]}$
• 参数：$W^{[l]}$、$b^{[l]}$

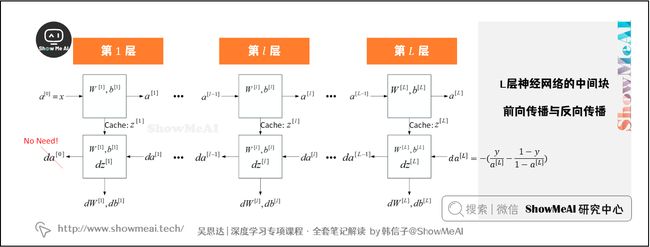
上面是第$l$层的流程块图，对于神经网络所有层，整体的流程块图前向传播过程和反向传播过程如下所示：

6.前向传播与反向传播

我们继续接着上一部分流程块图的内容，推导神经网络正向传播过程和反向传播过程的具体表达式。

6.1 前向传播过程

令层数为第$l$层，输入是$a^{[l-1]}$，输出是$a^{[l]}$，缓存变量是$z^{[l]}$。其表达式如下：

$$z^{[l]}=W^{[l]}{a}^{[l-1]}+b^{[l]}$$

$$a^{[l]}=g^{[l]}(z^{[l]})$$

$m$个训练样本的形态下，向量化形式为：

$$Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}$$

$$A^{[l]}=g^{[l]}(Z^{[l]})$$

6.2 反向传播过程

输入是$d{a}^{[l]}$，输出是$d{a}^{[l-1]}$、$d{W}^{[l]}$、$d{b}^{[l]}$。其表达式如下：

$$d{z}^{[l]}=d{a}^{[l]}\ast g^{[l]\prime }(z^{[l]})$$

$$d{W}^{[l]}=d{z}^{[l]}\cdot a^{[l-1]}$$

$$d{b}^{[l]}=d{z}^{[l]}$$

$$d{a}^{[l-1]}=W^{[l]T}\cdot d{z}^{[l]}$$

由上述第四个表达式可得$d{a}^{[l]}=W^{[l+1]T}\cdot d{z}^{[l+1]}$，将$d{a}^{[l]}$代入第一个表达式中可以得到：

$$d{z}^{[l]}=W^{[l+1]T}\cdot d{z}^{[l+1]}\ast g^{[l]\prime }(z^{[l]})$$

该式非常重要，反映了$d{z}^{[l+1]}$与$d{z}^{[l]}$的递推关系。

$m$个训练样本的形态下，向量化形式为：

$$d{Z}^{[l]}=d{A}^{[l]}\ast g^{[l]\prime }(Z^{[l]})$$

$$d{W}^{[l]}=\frac{1}{m}d{Z}^{[l]}\cdot A^{[l-1]T}$$

$$d{b}^{[l]}=\frac{1}{m}np.sum(d{Z}^{[l]},axis=1,keepdim=True)$$

$$d{A}^{[l-1]}=W^{[l]T}\cdot d{Z}^{[l]}$$

$$d{Z}^{[l]}=W^{[l+1]T}\cdot d{Z}^{[l+1]}\ast g^{[l]\prime }(Z^{[l]})$$

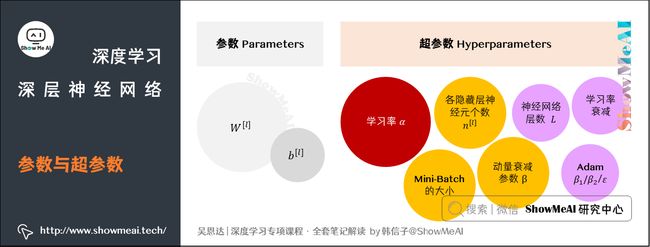
7.参数与超参数

神经网络中有两个大家要重点区分的概念：参数(parameters)和超参数(hyperparameters)。

• 神经网络中的参数就是我们熟悉的$W^{[l]}$和$b^{[l]}$。
• 神经网络的超参数是例如学习率$\alpha$，训练迭代次数$N$，神经网络层数$L$，各层神经元个数$n^{[l]}$，激活函数$g(z)$等。
• 之所以叫做超参数，是因为它们需要提前敲定，而且它们会决定参数$W^{[l]}$和$b^{[l]}$的值。

如何设置最优的超参数是一个比较困难的、需要经验知识的问题。通常的做法是选择超参数一定范围内的值，分别代入神经网络进行训练，测试cost function随着迭代次数增加的变化，根据结果选择cost function最小时对应的超参数值。这类似于机器学习中的实验验证的方法。(关于机器学习的模型评估详见 ShowMeAI文章图解机器学习 | 模型评估方法与准则)

8.神经网络vs人脑

神经网络跟人脑机制到底有什么联系呢？究竟有多少的相似程度？

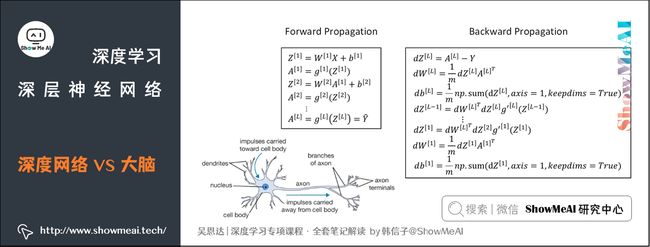
我们前面看到神经网络实际上可以分成两个部分：前向传播过程和反向传播过程。神经网络的每个神经元采用激活函数的方式，类似于感知机模型。这种模型与人脑神经元是类似的，但是一种非常简化的人脑神经元模型。

人脑神经元可分为树突、细胞体、轴突三部分。树突接收外界电刺激信号(类比神经网络中神经元输入)，传递给细胞体进行处理(类比神经网络中神经元激活函数运算)，最后由轴突传递给下一个神经元(类比神经网络中神经元输出)。

人脑神经元的结构和处理方式要复杂的多，神经网络模型只是非常简化的模型。

人脑如何进行学习？是否也是通过反向传播和梯度下降算法现在还不清楚，可能会更加复杂。这是值得生物学家探索的事情。

参考资料

• 图解机器学习 | 模型评估方法与准则

ShowMeAI系列教程推荐

• 大厂技术实现：推荐与广告计算解决方案
• 大厂技术实现：计算机视觉解决方案
• 大厂技术实现：自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读

推荐文章

• ShowMeAI 深度学习教程(1) | 深度学习概论
• ShowMeAI 深度学习教程(2) | 神经网络基础
• ShowMeAI 深度学习教程(3) | 浅层神经网络
• ShowMeAI 深度学习教程(4) | 深层神经网络
• ShowMeAI 深度学习教程(5) | 深度学习的实用层面
• ShowMeAI 深度学习教程(6) | 神经网络优化算法
• ShowMeAI 深度学习教程(7) | 网络优化：超参数调优、正则化、批归一化和程序框架
• ShowMeAI 深度学习教程(8) | AI应用实践策略（上）
• ShowMeAI 深度学习教程(9) | AI应用实践策略（下）
• ShowMeAI 深度学习教程(10) | 卷积神经网络解读
• ShowMeAI 深度学习教程(11) | 经典CNN网络实例详解
• ShowMeAI 深度学习教程(12) | CNN应用：目标检测
• ShowMeAI 深度学习教程(13) | CNN应用：人脸识别和神经风格转换
• ShowMeAI 深度学习教程(14) | 序列模型与RNN网络
• ShowMeAI 深度学习教程(15) | 自然语言处理与词嵌入
• ShowMeAI 深度学习教程(16) | Seq2seq序列模型和注意力机制