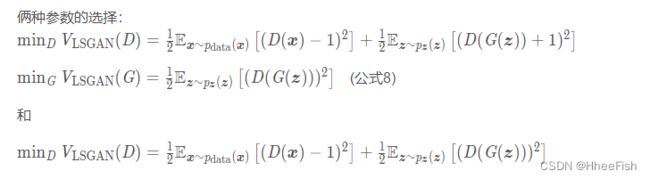生成式对抗网络(GANs)及变体

1.基础GAN

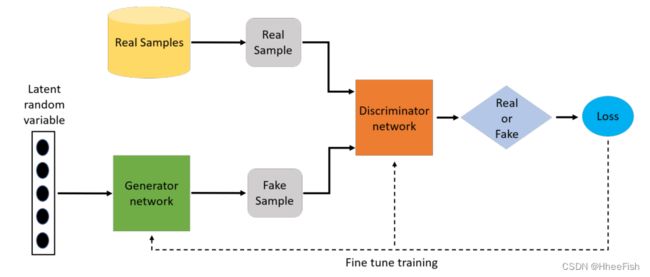
生成式对抗网络是Ian Goodfellow等人在2014年开发的。GANs属于生成模型。GANs是基于最小最大值和零和博弈理论。为此，GANs由两个神经网络组成:一个是Generator，另一个是Discriminator。生成器的目标是学习生成虚假的样本分布来欺骗鉴别器，而鉴别器的目标是学习区分生成器生成的真实分布和虚假分布。
GAN的总体结构由生成器和鉴别器组成，如图1所示。生成器(G)将一些随机噪声向量Z作为输入，然后尝试使用这个噪声向量G(Z)生成图像。然后将生成的图像传递给Discriminator，并根据Discriminator的输出更新Generator的参数。Discriminator (D)是一个二进制分类器，它同时查看生成器生成的真实样本和虚假样本，并试图决定哪些是真实的，哪些是虚假的。给定一个样本图像X，鉴别器模型的概率是虚假或真实的图像。然后将概率作为反馈传递回Generator。随着时间的推移，生成器和鉴别器模型都试图通过相互竞争来打败对方，这就是生成式对抗网络的术语“对抗性”的来源，优化是基于极大极小博弈问题。在训练过程中，Generator和Discriminator的参数都使用反向传播进行更新，生成器的最终目标是能够生成逼真的图像，而Discriminator的最终目标是逐步更好地从真实图像中检测生成的虚假图像。

GANs使用的是Goodfellow等人在首次引入GANs时引入的Minimax损失函数。生成器试图最小化下面的函数，而判别器试图最大化它。极小极大损失的表达式为:

在这里E_x是所有实际数据样本的期望值，D(x) 是鉴别器估计x是真的概率，G(z)是给定随机噪声矢量z作为输入的生成器输出，D(G(z))是鉴别器估计生成的假样本是真的的概率，E_z是生成机所有随机输入的期望值。

2.条件生成对抗网络(cGAN)

条件生成对抗网[118]或CGAN是GANs的扩展，用于条件样本生成。这可以控制生成数据的模式。CGAN使用一些额外的信息uy, 例如类标签或其他模式，通过连接这些额外信息和输入，并将其馈送到生成器G和鉴别器D。可以如下所示修改Minimax目标函数，

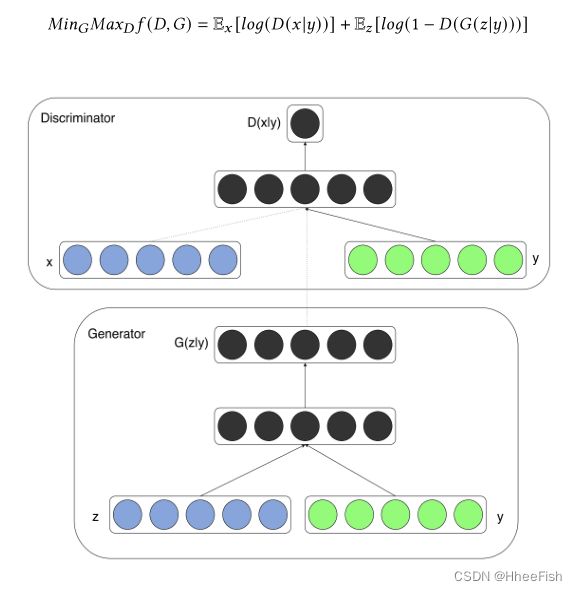
3.Wasserstein GAN (WGAN)

WGAN[7]的作者提出了一种新的算法，可以替代传统的GAN训练。他们表明，他们的新算法提高了模型学习的稳定性，并防止了模式崩溃等问题。对于批判模型，WGAN使用权值剪裁，这确保权值(模型参数)保持在预定义的范围内。作者发现Jensen-Shannon散度并不是测量不相交部分分布距离的理想方法。因此，他们使用了Wasserstein距离，该距离使用了Earth mover’s(EM)距离的概念，而不是测量生成的数据分布和真实数据分布之间的距离，在训练模型时试图保持One-Lipschitz连续性。

• 彻底解决GAN训练不稳定的问题，不再需要小心平衡生成器和判别器的训练程度
• 基本解决了collapse mode的问题，确保了生成样本的多样性
• 训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程，这个数值越小代表GAN训练得越好，代表生成器产生的图像质量越高（如题图所示）
• 以上一切好处不需要精心设计的网络架构，最简单的多层全连接网络就可以做到

最终给出了改进的算法实现流程，而改进后相比原始GAN的算法实现流程却只改了四点：

• 判别器最后一层去掉sigmoid
• 生成器和判别器的loss不取log
• 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
• 不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行

WAN-GP (improved WGAN)

部分参考：
W-GAN系 (Wasserstein GAN、 Improved WGAN)
DCGAN、WGAN、WGAN-GP、LSGAN、BEGAN原理总结及对比

WGAN-GP是WGAN之后的改进版，主要还是改进了连续性限制的条件，因为，作者也发现将权重剪切到一定范围之后，比如剪切到[-0.01,+0.01]后，发生了这样的情况，如下图左边表示

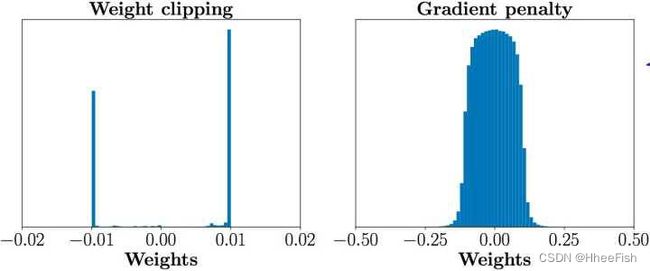
发现大多数的权重都在-0.01 和0.01上，这就意味了网络的大部分权重只有两个可能数，对于深度神经网络来说不能充分发挥深度神经网络的拟合能力，简直是极大的浪费。并且，也发现强制剪切权重容易导致梯度消失或者梯度爆炸，梯度消失很好理解，就是权重得不到更新信息，梯度爆炸就是更新过猛了，权重每次更新都变化很大，很容易导致训练不稳定。梯度消失与梯度爆炸原因均在于剪切范围的选择，选择过小的话会导致梯度消失，如果设得稍微大了一点，每经过一层网络，梯度变大一点点，多层之后就会发生梯度爆炸 。为了解决这个问题，并且找一个合适的方式满足lipschitz连续性条件，作者提出了使用梯度惩罚（gradient penalty）的方式以满足此连续性条件，其结果如上图右边所示。
梯度惩罚就是既然Lipschitz限制是要求判别器的梯度不超过K，那么可以通过建立一个损失函数来满足这个要求，即先求出判别器的梯度d(D(x))，然后建立与K之间的二范数就可以实现一个简单的损失函数设计。但是注意到D的梯度的数值空间是整个样本空间，对于图片（既包含了真实数据集也包含了生成出的图片集）这样的数据集来说，维度及其高，显然是及其不适合的计算的。作者提出没必要对整个数据集（真的和生成的）做采样，只要从每一批次的样本中采样就可以了，比如可以产生一个随机数，在生成数据和真实数据上做一个插值

所以WGAN-GP的贡献是：

• 提出了一种新的lipschitz连续性限制手法—梯度惩罚，解决了训练梯度消失梯度爆炸的问题。
• 比标准WGAN拥有更快的收敛速度，并能生成更高质量的样本
• 提供稳定的GAN训练方式，几乎不需要怎么调参，成功训练多种针对图片生成和语言模型的GAN架构

但是论文提出，由于是对每个batch中的每一个样本都做了梯度惩罚（随机数的维度是(batchsize，1)），因此判别器中不能使用batch norm,但是可以使用其他的normalization方法，比如Layer Normalization、Weight Normalization和Instance Normalization，论文中使用了Layer Normalization，weight normalization效果也是可以的。

3.Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks (DCGANs)

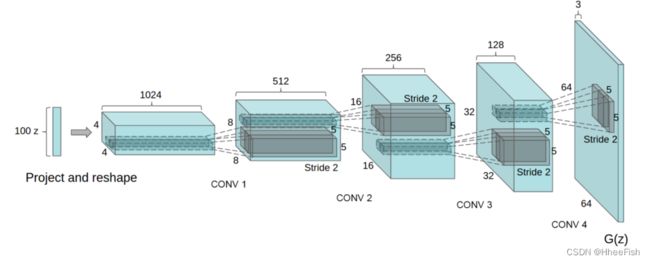
Radford等人[134]引入了深度卷积生成对抗网络(DCGANs)。顾名思义，DCGANs对生成器和鉴别器模型都使用深度卷积神经网络。最初的GAN架构只使用多层感知器或MLP，但由于CNN比MLP更擅长图像，DCGAN的作者在Generator G和Discriminator D神经网络架构中使用了CNN。以下列出了DCGANs神经网络体系结构的三个关键特性

• 首先，对于图所示的Generator，将卷积替换为转置后的卷积，因此Generator在每一层的表示依次变大，因为它从一个低维潜在向量映射到一个高维图像。用大步卷积(Discriminator)和部分大步卷积(Generator)替换任何池化层。
• 第二，在生成器和鉴别器中使用批处理归一化。
• 第三，在Generator中使用ReLU激活除输出使用Tanh外的所有层。在所有层的鉴别器中使用LeakyReLU激活。
• 第四，使用Adam优化器，而不是带有动量的SGD。

以上所有的修改都使DCGAN实现了稳定的训练。DCGAN很重要，因为作者证明，通过强制某些约束，我们可以开发出复杂的高质量生成器。作者还对普通GAN架构做了其他一些修改

4.Progressive Growing of GANs for Improved Quality, Stability, and Variation (ProGAN)

Karras等人[78]引入了一种新的训练方法，用于训练GAN生成高分辨率图像。ProGAN的想法是，通过在训练过程中逐渐增长的鉴别器和生成器网络，能够合成高分辨率和高质量的图像。ProGAN通过逐步训练Generator从低分辨率图像到高分辨率图像(参见图4)，使它更容易生成高分辨率的图像。在渐进式GAN中，生成器的第一层产生非常低分辨率的图像，随后的层增加细节。通过渐进式学习过程，训练相当稳定。

5.Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets (InfoGAN)

InfoGAN【19】背后的主要动机是使GANs能够学习解耦合的表示，并以无监督的方式控制生成图像的属性或特征。要执行此操作，而不是仅使用noize向量z作为输入，作者将噪声向量分解为两部分，第一部分是传统的噪声向量z第二个是新的“潜在代码向量”c. 此代码对输出图像有可预测的影响。InfoGAN【19】的目标函数如下所示

其中λ是正则化参数，I(c;G(z,c))是潜在代码c和生成器输出G(z,c)之间的互信息. 其思想是最大化潜在代码和生成器输出之间的互信息。这鼓励潜在代码c尽可能包含真实数据分布的重要相关特征。然而，计算互信息I(c;G(z,c))是不实际的，因为它需要后验信息P(c|x), 因此只能计算I(c;G(z,c))的近似值。这可以通过定义辅助分布Q(c|x)来估计P(c|x)的近似值。 因此，目标函数的最终形式由互信息的下界近似给出

6.Image-to-Image Translation with Conditional Adversarial Networks (pix2pix)

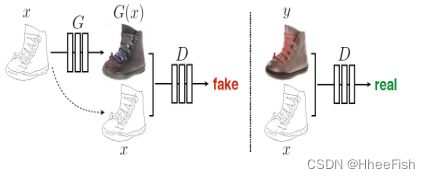
使用pix2pix将边缘映射到彩色图像[70]。D，鉴别器，学习区分伪元组(生成器生成)和实际元组(边缘，照片)。G，生成器，学习如何欺骗鉴别器。与无条件GAN相比，生成器和鉴别器都查看输入边图

pix2pix[70]是一种条件生成式对抗网络(cGAN[118])，用于解决通用的图像到图像的翻译问题。GAN由一个具有U-Net[137]架构的Generator和一个PatchGAN[70]分类器组成。pix2pix模型不仅学习从输入图像到输出图像的映射，而且构造一个损失函数来训练这种映射。有趣的是，不像常规的GANs, pix2pix生成器没有随机噪声向量输入。相反,生成机学习从输入图像x映射到输出图像G(x)。鉴别器的目标或损失函数是传统的对抗损失函数。生成器的另一方面是使用对抗训练的L1损失或生成的图像和真实图像/目标图像之间的像素距离损失来训练。퐿1损失仍鼓励特定输入生成的图像尽可能接近真实或地面实况图像对应的输出。这导致更快的收敛和更稳定的训练。条件GAN的损失函数：

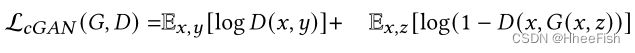
L1损失或图像间像素距离损失为:

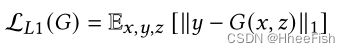
最终的优化目标为：

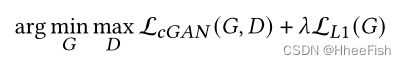
其中λ为超参数权重系数。Pix2PixHD[170]是Pix2Pix算法的改进版本。Pix2PixHD的主要目标是生成高分辨率的图像并执行语义操作。为此，作者引入了多尺度生成器和鉴别器，并结合了cga和特征匹配损失函数。训练集由一对对应的图像(s_i,x_i)，s_i是一个语义标签地图,x_i是相应的自然形象。cGAN损失函数为:

ith-layer特征提取器的鉴别器D_k为D_k^（i)(从输入到i层)。特征匹配损失L_FM(G,D_k):.

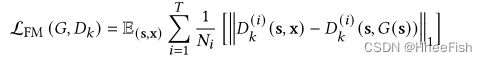
其中TT总层数，N_i表示在每一层的元素数量。给出了pix2pixHD的目标函数

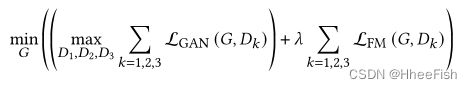
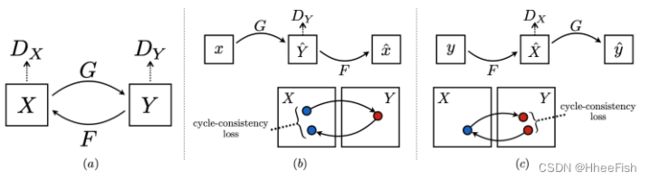
7.Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks(CycleGAN)

pix2pix的一个致命缺陷是，它需要成对的图像进行训练，因此不能用于没有输入和输出对的未配对数据。CycleGAN【197】通过引入循环一致性损失来解决这个问题，该损失试图在一个周期的翻译和反向翻译后保留原始图像。在此公式中，不再需要匹配图像对进行训练。CycleGAN使用两个生成器和两个鉴别器。生成器G用于将图像从X域转换到Y域。另一方面，生成器F将图像从Y转换为X(G: X->Y; F: Y->X). 鉴别器D_y区分y和G(x)和鉴别器D_X区分x和G(y). 对抗性损失适用于两个映射函数。对于映射函数G : X →Y及其鉴别器D_Y , 目标函数如下所示


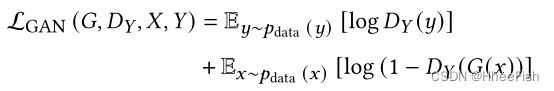
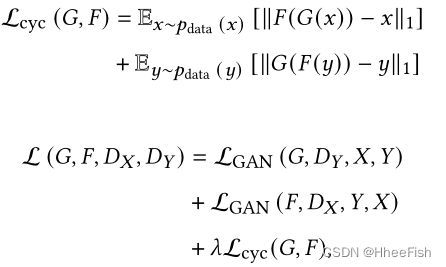
λ控制两个目标的相对重要性

8.A Style-Based Generator Architecture for Generative Adversarial Networks(StyleGAN)

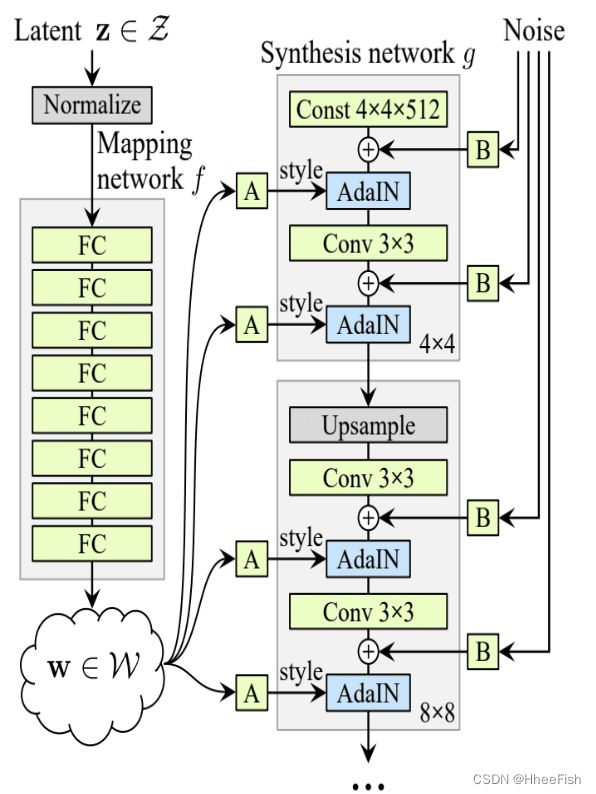
StyleGAN[80]的主要目标是产生高质量、高分辨率的面部图像，这些图像在本质上是多样化的，并提供对生成的合成图像风格的控制。StyleGAN是ProGAN[78]模型的扩展，ProGAN模型在训练过程中，通过Discriminator和Generator网络的增量(逐渐)增长，采用渐进式增长的方法合成高分辨率和高质量的图像。需要注意的是，StyleGAN的变化只影响Generator网络，这意味着它们只影响生成过程。与传统GAN相同的Discriminator和loss函数并没有改变。升级后的Generator包括对ProGAN的Generator的几个添加，如图8所示。并描述如下:

• 基线渐进式GAN：作者使用渐进式GAN（ProGAN[78]）作为基线，从中继承网络架构和一些超参数
• 双线性上/下采样：ProGAN模型使用最近邻上/下采样，但StyleGAN的作者对生成器和鉴别器都使用双线性采样层
• 映射网络、样式网络和AdaIN：代替输入噪声向量푧 它直接进入生成器，通过映射网络获得中间噪声向量푤z。映射网络的输出(w) 通过学习的仿射变换（A），然后通过自适应实例规范化（68）或AdaIN模块进入合成网络。在图中，“A”代表学习的仿射变换。AdaIN模块传输由映射网络在仿射变换后创建的编码信息，这些信息在卷积层之后被合并到生成器模型的每个块中。AdaIN模块首先将特征映射的输出转换为标准高斯，然后添加样式向量作为偏差项。映射网络f是一个标准的深度神经网络，由8个完全连接的层和合成网络g组成由18层组成
• 删除传统输入：包括ProGAN在内的大多数模型都使用随机输入来生成生成器的初始图像。然而，StyleGAN的作者发现，图像特征由푤 还有亚当。因此，他们通过消除传统的输入层来简化体系结构，并使用学习到的常量张量开始图像合成
• 添加噪声输入：在评估非线性之前，在每次卷积之后添加高斯噪声。如图所示。“B”是每个通道应用于噪声输入的学习比例因子
• 混合正则化：作者还介绍了一种新的正则化方法，以减少相邻样式的相关性，并对生成的图像进行更细粒度的控制。而不是只传递一个潜在向量z, 通过映射网络作为输入，得到一个向量w, 作为输出，混合正则化传递两个潜在向量，z1和z2，通过映射向量得到两个向量，w1和w2。使用的w1和w2对于每次迭代都是完全随机的。这种技术可以防止网络假设相邻的样式相互关联。
  

9.Recurrent GAN (RGAN) and Recurrent Conditional GAN (RCGAN)

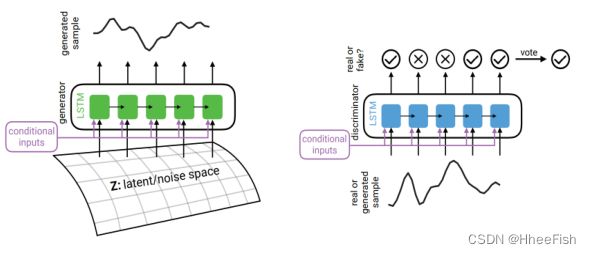
除生成合成图像外，GAN还可以生成顺序数据[38,119]。而不是建模数据分布在原始特征空间中,时间序列数据的生成模型也捕捉到了条件分布P(X_t|X_1:t−1)给定的历史数据。循环神经网络与传统神经网络在结构上的主要区别在于，我们在生成器和鉴别器上都用循环神经网络(RNNs)取代了DNNs/ CNNs。这里，RNN可以是RNN的任何变体，如长短期记忆(LSTM)和门控循环单元(GRU)，它捕捉输入数据的时间依赖性。在循环条件GAN (RCGAN)中，Generator和Discriminator都以一些辅助信息为条件。[38]实验表明，RGAN和RCGAN能够有效地生成真实的时间序列合成数据。
我们阐述了RGAN和RCGAN的架构。生成器RNN在每个时间步取随机噪声生成合成序列。然后，判别器RNN作为分类器来区分输入的真伪。如果是RCGAN，条件输入连接到生成器和鉴别器的顺序输入。与GAN类似，RGAN中的Discriminator最大限度地减少了生成数据与真实数据之间的交叉熵损失。判别器损耗公式如下:

其中，X_n (X_n∈ R^T×d) 和y_n (y_n∈ {1,0}^T) 是鉴别器的输入和输出，具有序列长度T和特征尺寸d。y_n 对于实数序列是1向量，对于合成序列是0向量。CE(·)是平均交叉熵函数RNN_D(·)是RNN的鉴别器。生成器损耗公式如下：

Z_n∈ R^T×m是随机噪声向量. 在RCGAN的情况下，生成器和鉴别器的输入也串联了条件信息c_n在每个时间步:

10.LSGAN（Least Square GAN）

部分参考：
CSDN:LSGAN (Least Squares Generative Adversarial Networks)
知乎：LSGAN——最小二乘GAN

最小二乘GAN，目标函数将是一个平方误差，考虑到D网络的目标是分辨两类，如果给生成样本和真实样本分别编码为a,b，那么采用平方误差作为目标函数，D的目标就是

G的目标函数将编码a换成编码c，这个编码表示D将G生成的样本当成真实样本，

作者列出了传统的GAN其实在优化的是JS散度,因此，对于作者提出的LSGANs, 研究了LSGANs损失函数和f散度 (f-divergence)之间的联系,避免了使用JS散度下造成的梯度为0，其中需要满足b-c=1 且b-a=2