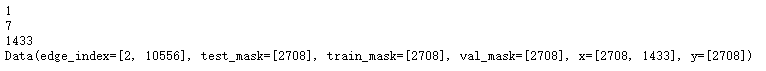图结构数据及环境配置

1. 引言

图表描述了实体之间的成对关系，是来自社会科学、语言学、化学、生物学和物理学等许多不同领域的现实世界数据的重要表示。图形在社会科学中被广泛地用来表示个体之间的关系。在化学中，化合物被表示为图，其中原子为节点，化学键为边(Bonchev，1991)。在语言学中，图形被用来捕捉句子的句法和组合结构。例如，根据某些上下文无关文法，使用解析树来表示句子的句法结构，而抽象意义表示(Abstract Meaning Representation，AMR)将句子的意义编码为有根有向图(banarscu et al. ，2013)。因此，图形的研究引起了多学科的广泛关注。

2. 图表示法

在本节中，我们介绍图的定义。我们将重点讨论简单的未加权图，并将在以下部分讨论更复杂的图。

定义一（图）：

• 一个图被记为$\mathcal{G}=\mathcal{V},\mathcal{E}$，其中
  $\mathcal{V}=\{v_1,\dots ,v_N\}$ 是数量为$N=|\mathcal{V}|$ 的结点的集合，
  $\mathcal{E}=\{e_1,\dots ,e_M\}$ 是数量为 $M$ 的边的集合。
• 图用节点表示实体（entities ），用边表示实体间的关系（relations）。
• 节点和边的信息可以是类别型的（categorical），类别型数据的取值只能是哪一类别。一般称类别型的信息为标签（label）。
• 节点和边的信息可以是数值型的（numeric），数值型数据的取值范围为实数。一般称数值型的信息为属性（attribute）。
• 大部分情况中，节点含有信息，边可能含有信息。

定义二（图的邻接矩阵）：

• 给定一个图$\mathcal{G}=\mathcal{V},\mathcal{E}$，其对应的邻接矩阵被记为$\mathbf{A}\in {\{0,1\}}^{N\times N}$。${\mathbf{A}}_{i,j}=1$表示存在从结点$v_i$到$v_j$的边，反之表示不存在从结点$v_i$到$v_j$的边。
• 在无向图中，从结点$v_i$到$v_j$的边存在，意味着从结点$v_j$到$v_i$的边也存在。因而无向图的邻接矩阵是对称的。
• 在无权图中，各条边的权重被认为是等价的，即认为各条边的权重为$1$。
• 对于有权图，其对应的邻接矩阵通常被记为$\mathbf{W}\in {\{R\}}^{N\times N}$，其中${\mathbf{W}}_{i,j}=w_{ij}$表示从结点$v_i$到$v_j$的边的权重。若边不存在时，边的权重为$0$。

一个无向无权图的例子：

其邻接矩阵为：
$$\left(\begin{array}{ccccc}0& 1& 0& 1& 1\\ 1& 0& 1& 0& 0\\ 0& 1& 0& 0& 1\\ 1& 0& 0& 0& 1\\ 1& 0& 1& 1& 0\end{array}\right)$$

3. 图的属性

定义三（结点的度，degree）：

• 对于有向有权图，结点$v_i$的出度（out degree）等于从$v_i$出发的边的权重之和，结点$v_i$的入度（in
  degree）等于从连向$v_i$的边的权重之和。
• 无向图是有向图的特殊情况，结点的出度与入度相等。
• 无权图是有权图的特殊情况，各边的权重为$1$，那么结点$v_i$的出度（out degree）等于从$v_i$出发的边的数量，结点$v_i$的入度（in degree）等于从连向$v_i$的边的数量。
• 结点$v_i$的度记为$d(v_i)$，入度记为$d_{in}(v_i)$，出度记为$d_{out}(v_i)$。

定义四（邻接结点，neighbors）：

• 结点$v_i$的邻接结点为与结点$v_i$直接相连的结点，其被记为$\mathcal{N}(v_i)$。
• 结点$v_i$的$k$跳远的邻接节点（neighbors with $k$-hop）指的是到结点$v_i$要走$k$步的节点（一个节点的$2$跳远的邻接节点包含了自身）。

定义五（行走，walk）：

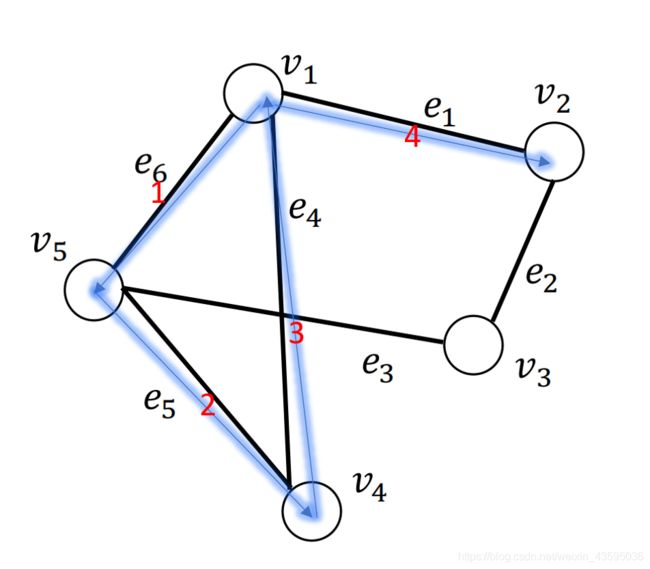
• $walk(v_1,v_2)=(v_1,e_6,e_5,e_4,e_1,v_2)$，这是一次“行走”，它是一次从节点$v_1$出发，依次经过边$e_6,e_5,e_4,e_1$，最终到达节点$v_2$的“行走”。
• 下图所示为$walk(v_1,v_2)=(v_1,e_6,e_5,e_4,e_1,v_2)$，其中红色数字标识了边的访问序号。
• 在“行走”中，节点是运行重复的。

定理六：

• 有一图，其邻接矩阵为 $\mathbf{A}$,
  ${\mathbf{A}}^n$为邻接矩阵的$n$次方，那么${\mathbf{A}}^n[i,j]$等于从结点$v_i$到结点$v_j$的长度为$n$的行走的个数。

定义七（路径，path）：

• “路径”是结点不可重复的“行走”。

定义八（子图，subgraph）：

• 有一图$\mathcal{G}=\mathcal{V},\mathcal{E}$，另有一图${\mathcal{G}}^{\prime }={\mathcal{V}}^{\prime },{\mathcal{E}}^{\prime }$，其中${\mathcal{V}}^{\prime }\in \mathcal{V}$，${\mathcal{E}}^{\prime }\in \mathcal{E}$并且${\mathcal{V}}^{\prime }$不包含${\mathcal{E}}^{\prime }$中未出现过的结点，那么${\mathcal{G}}^{\prime }$是$\mathcal{G}$的子图。

定义九（连通分量，connected component）：

• 给定图${\mathcal{G}}^{\prime }={\mathcal{V}}^{\prime },{\mathcal{E}}^{\prime }$是图$\mathcal{G}=\mathcal{V},\mathcal{E}$的子图。记属于图$\mathcal{G}$但不属于${\mathcal{G}}^{\prime }$图的结点集合记为$\mathcal{V}/{\mathcal{V}}^{\prime }$
  。如果属于${\mathcal{V}}^{\prime }$的任意结点对之间存在至少一条路径，但不存在一条边连接属于${\mathcal{V}}^{\prime }$的结点与属于$\mathcal{V}/{\mathcal{V}}^{\prime }$的结点，那么图${\mathcal{G}}^{\prime }$是图$\mathcal{G}$的连通分量。
  
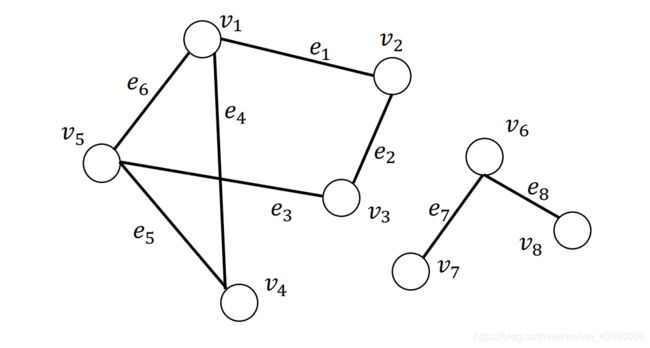
  左右两边子图都是整图的连通分量。

定义十（连通图，connected graph）：

• 当一个图只包含一个连通分量，即其自身，那么该图是一个连通图。

定义十一（最短路径，shortest path）：

• $v_s,v_t\in \mathcal{V}$ 是图$\mathcal{G}=\mathcal{V},\mathcal{E}$上的一对结点，结点对$v_s,v_t\in \mathcal{V}$之间所有路径的集合记为$\mathcal{P}\mathrm{s}\mathrm{t}$。结点对$v_s,v_t$之间的最短路径$p_{\mathrm{s}t}^{\mathrm{s}\mathrm{p}}$为${\mathcal{P}}_{\mathrm{s}\mathrm{t}}$中长度最短的一条路径，其形式化定义为 $$p_{\mathrm{s}t}^{\mathrm{s}\mathrm{p}}=\arg \min p\in \mathcal{P}\mathrm{s}\mathrm{t}|p|$$
  其中，$p$表示${\mathcal{P}}_{\mathrm{s}\mathrm{t}}$中的一条路径，$|p|$是路径$p$的长度。

定义十二（直径，diameter）：

• 给定一个连通图$\mathcal{G}=\mathcal{V},\mathcal{E}$，其直径为其所有结点对之间的最短路径的最大值，形式化定义为 $$\mathrm{diameter}(\mathcal{G})=\underset{v_s,v_t\in \mathcal{V}}{\max }\underset{p\in \mathcal{P}st}{\min }|p|$$

定义十三（拉普拉斯矩阵，Laplacian Matrix）：

• 给定一个图$\mathcal{G}=\mathcal{V},\mathcal{E}$，其邻接矩阵为$A$，其拉普拉斯矩阵定义为$\mathbf{L}=\mathbf{D}-\mathbf{A}$，其中$\mathbf{D}=\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}(\mathbf{d}({\mathbf{v}}_1),\cdots ,\mathbf{d}({\mathbf{v}}_{\mathbf{N}}))$。

定义十四（对称归一化的拉普拉斯矩阵，Symmetric normalized Laplacian）：

• 给定一个图$\mathcal{G}=\mathcal{V},\mathcal{E}$，其邻接矩阵为$A$，其规范化的拉普拉斯矩阵定义为 $$\mathbf{L}={\mathbf{D}}^{-\frac{1}{2}}(\mathbf{D}-\mathbf{A}){\mathbf{D}}^{-\frac{1}{2}}=\mathbf{I}-{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}$$

4. 图的种类

4.1 异质图

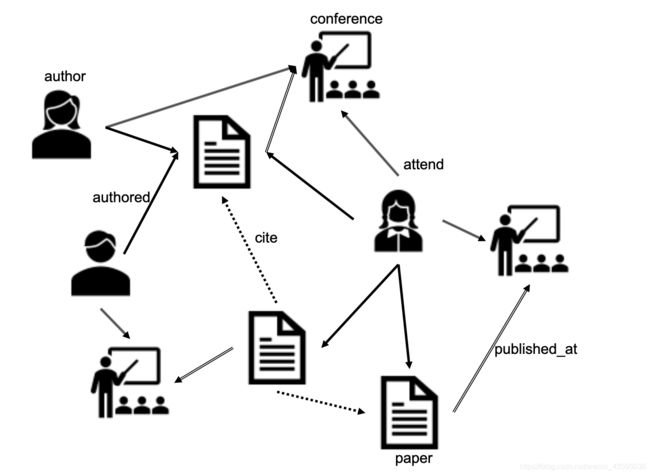
我们讨论的简单图是齐次图。它们只有一种类型的节点和一种类型的边。然而，在许多实际应用程序中，我们希望为多种类型的节点之间的多种类型的关系建模。如下图所示，在描述出版物和引用的学术网络中，有三种类型的节点，包括作者、论文和场所。还有各种各样的边，表示节点之间的不同关系。例如，论文或论文边之间的引用关系存在边，表示作者与论文之间的作者关系。接下来，我们定义异构图为存在多种类型的节点和多种类型的边的图。

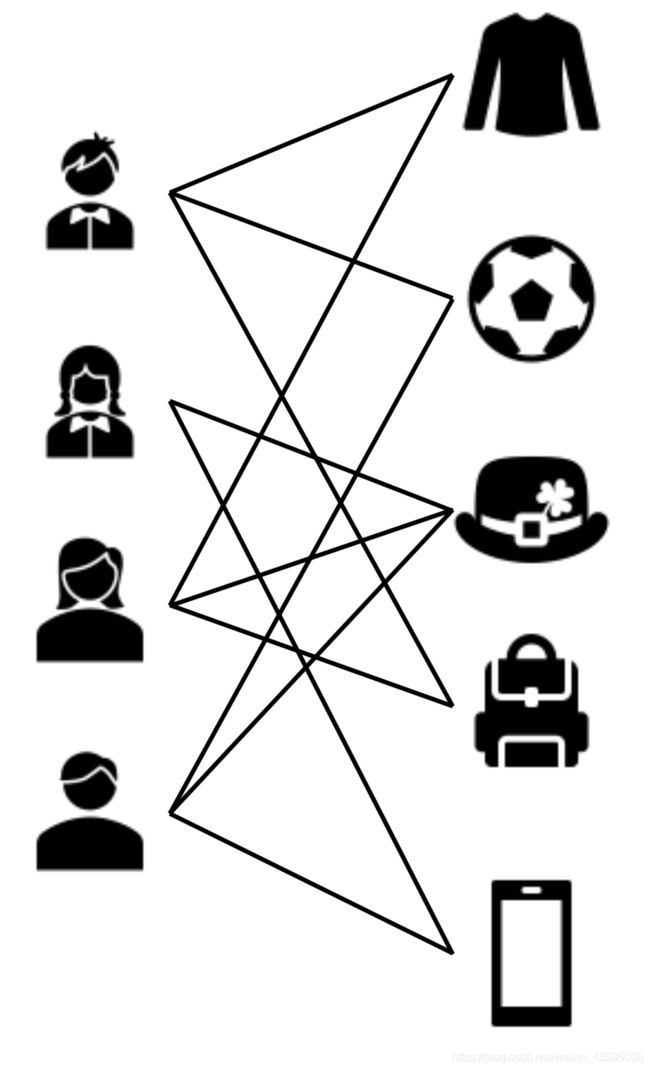
4.2 二部图

节点分为两类，只有不同类的节点之间存在边。

5. 图的计算任务

有各种各样的计算任务提出了图。这些任务主要可以分为两类。一种是以节点为中心的任务，其中整个数据通常表示为一个图，节点作为数据样本。另一种是以图为中心的任务，其中数据通常由一组图形组成，每个数据样本都是一个图形。在这一部分中，我们简要介绍了每个组的代表性任务。

5.1 以节点为中心的任务

许多以节点为中心的任务已经得到了广泛的研究，如节点分类、节点排序、链路预测和社区检测。接下来，我们讨论了两个典型的任务，包括节点分类和链路预测。

节点分类

在许多真实世界的图中，节点与有用的信息相关联，通常被视为这些节点的标签。例如，在社交网络中，这些信息可以是用户的人口统计属性，如年龄、性别、职业或用户的兴趣和爱好。这些标签通常有助于描述节点的特征，可以用于许多重要的应用程序。例如，在 Facebook 等社交媒体中，可以利用与兴趣和爱好相关的标签向用户推荐相关项目(例如，新闻和事件)。然而，在现实中，通常很难为所有节点获得完整的标签集。例如，只有不到1% 的 Facebook 用户提供了他们完整的人口统计特征。因此，我们可能给出一个只有部分节点与标签相关联的图，并且我们的目标是推断没有标签的节点的标签。提出了图的节点分类问题。

例子(Flickr 中的 Node Classification)
Flickr 是一个图片托管平台，允许用户托管他们的照片。它也是一个在线社交社区，用户可以互相关注。因此，Flickr 上的用户和他们之间的联系形成了一个图表。此外，Flickr 上的用户还可以订阅“黑与白”、“雾与雨”和“狗的世界”等兴趣小组。这些订阅表明用户的兴趣，可以用作他们的标签。用户可以订阅多个组。因此，每个用户都可以与多个标签关联。图形扫描中的多标签节点分类问题有助于预测用户感兴趣但尚未订阅的潜在群组。在 Flickr 上可以找到这样的一个数据集(Tang and Liu，2009)。

链接预测

在许多实际应用中，图是不完整的，但是缺少边。有些联系是存在的。然而，它们没有被观察到或记录下来，这就导致了被观察图中的边丢失。同时，许多图形也在自然演化。在 Facebook 这样的社交媒体中，用户可以不断地与其他用户成为朋友。在学术合作图中，给定的作者可以不断地与其他作者建立新的合作关系。推断或预测这些缺失的边可以有益于许多应用，如朋友推荐(Adamic and Adar，2003) ，知识图完成(Nickel 等人，2015) ，以及犯罪情报分析(Berlusconi 等人，2016)。

例子(预测 DBLP 中出现的合作)
DBLP 是一个在线计算机科学书目网站，提供了一个计算机科学研究论文的综合列表。以作者为节点的 DBLP 论文可以构造一个共同作者图，如果作者在 DBLP 中至少共同作者了一篇论文，则可以认为作者是连通的。预测以前从未合作过的作者之间的新合作是一个有趣的链接预测问题。一个用于链接预测研究的大型 DBLP 合作数据集可以在(杨和 Leskovec，2015年)中找到。

5.2 以图为中心的任务

图的分类、图匹配和图生成是许多以图为中心的任务。接下来，我们讨论最具代表性的以图为中心的任务，即图分类。

图分类

节点分类将图中的每个节点视为一个数据样本，目的是为这些未标记的节点分配标签。在某些应用程序中，每个示例都可以表示为一个图。例如，在化学信息学中，化学分子可以表示为图，其中原子是节点，化学键在它们之间是边。这些化学分子可能具有不同的性质，如溶解性和毒性，可以作为它们的标签。实际上，我们可能想自动预测新发现的化学分子的这些性质。这一目标可以通过图分类任务来实现，该任务的目的是预测未标记图的标签。由于图形结构的复杂性，传统的图形分类方法无法进行图形分类。因此，需要专注的努力。

例子(将蛋白质分类为酶或非酶)
蛋白质可以用图表示，其中氨基酸是节点，如果两个节点之间的距离小于6埃，则形成两个节点之间的边。酶是一类作为生物催化剂催化生化反应的蛋白质。给定一个蛋白质，预测它是否是一种酶可以被视为一个图形分类任务，其中每个蛋白质的标签是酶或非酶。

6. 图神经网络学习面临的挑战

在学习了简单的图论知识，我们再来回顾应用神经网络于图面临的挑战。
过去的深度学习应用中，我们主要接触的数据形式主要是这四种：矩阵、张量、序列（sequence）和时间序列（time series），它们都是规则的结构化的数据。然而图数据是非规则的非结构化的，它具有以下的特点：

1. 任意的大小和复杂的拓扑结构；
2. 没有固定的节点排序或参考点；
3. 通常是动态的，并具有多模态的特征；
4. 图的信息并非只蕴含在节点信息和边的信息中，图的信息还包括了图的拓扑结构。

以往的深度学习技术是为规则且结构化的数据设计的，无法直接用于图数据。应用于图数据的神经网络，要求

• 适用于不同度的节点；
• 节点表征的计算与邻接节点的排序无关；
• 不但能够根据节点信息、邻接节点的信息和边的信息计算节点表征，还能根据图拓扑结构计算节点表征。

下面的图片展示了一个需要根据图拓扑结构计算节点表征的例子。图片中展示了两个图，它们同样有俩黄、俩蓝、俩绿，共6个节点，因此它们的节点信息相同；假设边两端节点的信息为边的信息，那么这两个图有一样的边，即它们的边信息相同。但这两个图是不一样的图，它们的拓扑结构不一样。

7. 环境配置

PyTorch Geometric (PyG)是面向几何深度学习的PyTorch的扩展库，几何深度学习指的是应用于图和其他不规则、非结构化数据的深度学习。基于PyG库，我们可以轻松地根据数据生成一个图对象，然后很方便的使用它；我们也可以容易地为一个图数据集构造一个数据集类，然后很方便的将它用于神经网络。

7.1 安装pytorch

首先将anconda的安装源修改为清华的镜像源：

• conda config --add channels
  https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/msys2/
• conda config --add channels
  https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/conda-forge/
• conda config --add channels
  https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/
• conda config --add channels
  https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/pytorch/
• conda config --set show_channel_urls yes

然后进入 PyTorch 官网，选择适合版本。

最下面为conda安装命令：
conda install pytorch torchvision torchaudio cpuonly -c pytorch
去掉最后的-c pytorch，即可从清华源下载安装。

7.2 安装正确版本的PyG

• pip install torch-scatter -f
  https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
• pip install torch-sparse -f
  https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
• pip install torch-cluster -f
  https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
• pip install torch-spline-conv -f
  https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
• pip install torch-geometric

8. Data类——PyG中图的表示及其使用

Data对象的创建通过构造函数

Data类的构造函数：
class Data(object):

   def __init__(self, x=None, edge_index=None, edge_attr=None, y=None, **kwargs):
    r"""
    Args:
        x (Tensor, optional): 节点属性矩阵，大小为`[num_nodes, num_node_features]`
        edge_index (LongTensor, optional): 边索引矩阵，大小为`[2, num_edges]`，第0行为尾节点，第1行为头节点，头指向尾
        edge_attr (Tensor, optional): 边属性矩阵，大小为`[num_edges, num_edge_features]`
        y (Tensor, optional): 节点或图的标签，任意大小（，其实也可以是边的标签）
	
    """
    self.x = x
    self.edge_index = edge_index
    self.edge_attr = edge_attr
    self.y = y

    for key, item in kwargs.items():
        if key == 'num_nodes':
            self.__num_nodes__ = item
        else:
            self[key] = item

edge_index的每一列定义一条边，其中第一行为边起始节点的索引，第二行为边结束节点的索引。这种表示方法被称为COO格式（coordinate format），通常用于表示稀疏矩阵。PyG不是用稠密矩阵$\mathbf{A}\in {0,1}^{|\mathcal{V}|\times |\mathcal{V}|}$来持有邻接矩阵的信息，而是用仅存储邻接矩阵$\mathbf{A}$中非$0$元素的稀疏矩阵来表示图。

通常，一个图至少包含x, edge_index, edge_attr, y, num_nodes 5个属性，当图包含其他属性时，我们可以通过指定额外的参数使Data对象包含其他的属性：

graph = Data(x=x, edge_index=edge_index, edge_attr=edge_attr, y=y, num_nodes=num_nodes, other_attr=other_attr)

转dict对象为Data对象

我们也可以将一个dict对象转换为一个Data对象：

graph_dict = {
    'x': x,
    'edge_index': edge_index,
    'edge_attr': edge_attr,
    'y': y,
    'num_nodes': num_nodes,
    'other_attr': other_attr
}
graph_data = Data.from_dict(graph_dict)

from_dict是一个类方法：

@classmethod
def from_dict(cls, dictionary):
    r"""Creates a data object from a python dictionary."""
    data = cls()
    for key, item in dictionary.items():
        data[key] = item

    return data

注意：graph_dict中属性值的类型与大小的要求与Data类的构造函数的要求相同。

Data对象转换成其他类型数据

我们可以将Data对象转换为dict对象：

def to_dict(self):
    return {key: item for key, item in self}

或转换为 namedtuple：

def to_namedtuple(self):
    keys = self.keys
    DataTuple = collections.namedtuple('DataTuple', keys)
    return DataTuple(*[self[key] for key in keys])

获取Data对象属性

x = graph_data['x']

设置Data对象属性

graph_data['x'] = x

获取Data对象包含的属性的关键字

graph_data.keys()

对边排序并移除重复的边

graph_data.coalesce()

Data对象的其他性质

我们通过观察PyG中内置的一个图来查看Data对象的性质：

from torch_geometric.datasets import KarateClub

dataset = KarateClub()
data = dataset[0]  # Get the first graph object.
print(data)
print('==============================================================')

# 获取图的一些信息
print(f'Number of nodes: {data.num_nodes}') # 节点数量
print(f'Number of edges: {data.num_edges}') # 边数量
print(f'Number of node features: {data.num_node_features}') # 节点属性的维度
print(f'Number of node features: {data.num_features}') # 同样是节点属性的维度
print(f'Number of edge features: {data.num_edge_features}') # 边属性的维度
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}') # 平均节点度
print(f'if edge indices are ordered and do not contain duplicate entries.: {data.is_coalesced()}') # 是否边是有序的同时不含有重复的边
print(f'Number of training nodes: {data.train_mask.sum()}') # 用作训练集的节点
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}') # 用作训练集的节点数占比
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}') # 此图是否包含孤立的节点
print(f'Contains self-loops: {data.contains_self_loops()}')  # 此图是否包含自环的边
print(f'Is undirected: {data.is_undirected()}')  # 此图是否是无向图

9. Dataset类——PyG中图数据集的表示及其使用

PyG内置了大量常用的基准数据集，接下来我们以PyG内置的Planetoid数据集为例，来学习PyG中图数据集的表示及使用。

Planetoid数据集类的官方文档为torch_geometric.datasets.Planetoid。

生成数据集对象并分析数据集

如下方代码所示，在PyG中生成一个数据集是简单直接的。在第一次生成PyG内置的数据集时，程序首先下载原始文件，然后将原始文件处理成包含Data对象的Dataset对象并保存到文件。因为github网站在中国不易访问，所以在代码里修改了访问地址。

from torch_geometric.datasets import Planetoid
Planetoid.url ='https://gitee.com/rongqinchen/planetoid/tree/master/data'
dataset = Planetoid(root='dataset/Cora', name='Cora')
print(len(dataset))
print(dataset.num_classes)
print(dataset.num_node_features)
print(dataset[0])

分析数据集中样本

可以看到该数据集只有一个图，包含7个分类任务，节点的属性为1433维度。

data = dataset[0]
print(data.is_undirected())
print(data.train_mask.sum().item())
print(data.val_mask.sum().item())
print(data.test_mask.sum().item())

现在我们看到该数据集包含的唯一的图，有2708个节点，节点特征为1433维，有10556条边，有140个用作训练集的节点，有500个用作验证集的节点，有1000个用作测试集的节点。

数据集的使用

假设我们定义好了一个图神经网络模型，其名为Net。在下方的代码中，我们展示了节点分类图数据集在训练过程中的使用。

model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

10. 作业

• 请通过继承Data类实现一个类，专门用于表示“机构-作者-论文”的网络。该网络包含“机构“、”作者“和”论文”三类节点，以及“作者-机构“和“作者-论文“两类边。对要实现的类的要求：1）用不同的属性存储不同节点的属性；2）用不同的属性存储不同的边（边没有属性）；3）逐一实现获取不同节点数量的方法。

class Data(object):
    def __init__(self, x=None, edge_index=None, edge_attr=None, y=None, **kwargs):
    
#     Args:
#         x (Tensor, optional): 节点属性矩阵，大小为`[num_nodes, num_node_features]`
#         edge_index (LongTensor, optional): 边索引矩阵，大小为`[2, num_edges]`，第0行为尾节点，第1行为头节点，头指向尾
#         edge_attr (Tensor, optional): 边属性矩阵，大小为`[num_edges, num_edge_features]`
#         y (Tensor, optional): 节点或图的标签，任意大小（，其实也可以是边的标签）
        self.x = x
        self.edge_index = edge_index
        self.edge_attr = edge_attr
        self.y = y

        for key, item in kwargs.items():
            if key == 'num_nodes':
                self.__num_nodes__ = item
            else:
                self[key] = item

class graph(Data):
    def __init__(self, paper_x=None, author_x=None, institution_x=None,
                 write_edge_index=None, contribute_edge_index=None,
                 write_edge_attr=None, contribute_attr=None, 
                 x=None, edge_index=None, edge_attr=None, y=None, **kwargs):
        super(graph, self).__init__(x=None, edge_index=None, edge_attr=None, y=None, **kwargs)
        self.paper_x = paper_x
        self.author_x = author_x
        self.institution_x = institution_x
        self.write_edge_index = write_edge_index
        self.contribute_edge_index = contribute_edge_index
        self.write_edge_attr = write_edge_attr
        self.contribute_attr = contribute_attr
        
    def num_paper_x():
        return self_paper_x.shape[0]
    
    def num_author_x():
        return self_author_x.shape[0]
    
    def num_institution_x():
        return self_institution_x.shape[0]

参考资料
https://github.com/datawhalechina/team-learning-nlp/blob/master/GNN
感谢Datawhale对开源学习的贡献！