Tableau 十四、回归分析与时间序列分析

1.回归分析

1.1线性回归模型及参数解释

回归分析是将可能存在相关关系的变量拟合成直线或者曲线，然后据此一方面总结已有数据的规律和特征，另一方面预测数据。

导入数据“人工坐席接听数据.xlsx”

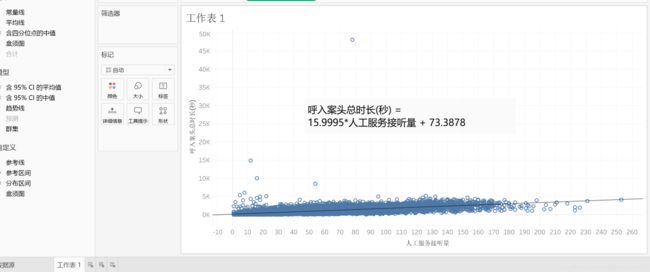
在工作表1，将【人工服务接听量】放入【列】，将【呼入案头总时长(秒)】放入【行】。

点击【分析】，取消【聚合度量】的勾选。

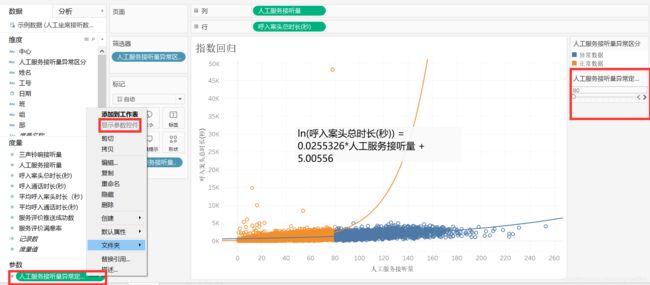
第一种添加趋势线方式

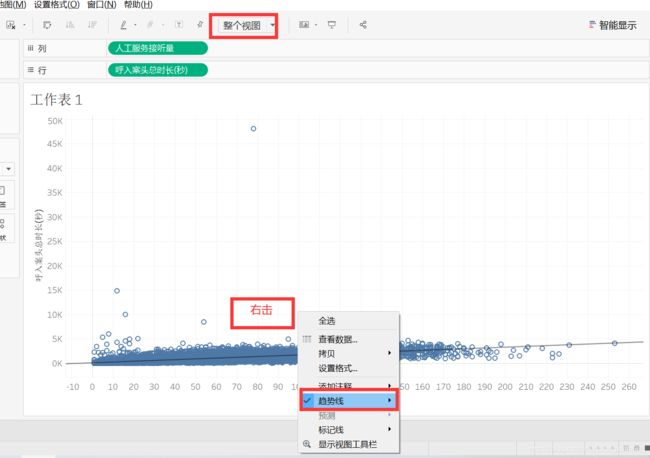
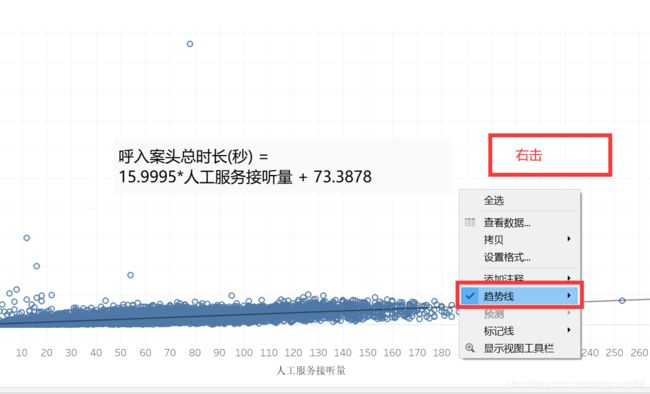
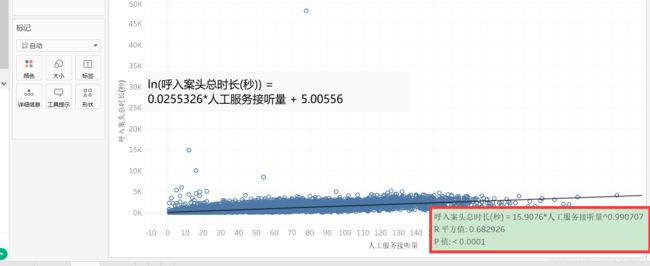
选择【整个视图】，右击图表——【趋势线】——【显示趋势线】。这样就添加好了线性回归模型。

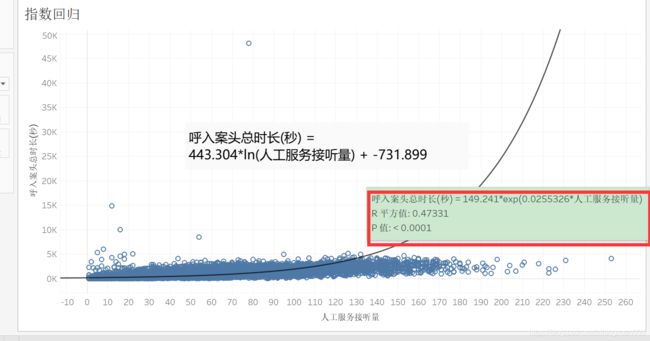
将鼠标悬浮在趋势线上，会出现提示框。

参数解释

线性回归就是一次方程，比如y=nx+b

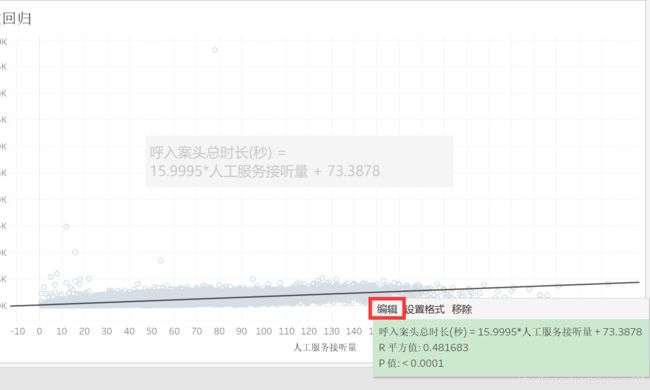
R值就是拟合优度，越大越好，R平方值范围是0—1，一般认为0.1上都可以，越大越好。

P值越小越好，常规设置是<0.05，可以调整。P值决定了系数，比如提示框里15.9995的核心程度。

第二种添加趋势线方式

【分析】——【趋势线】——【显示趋势线】。

第三种添加趋势线方式

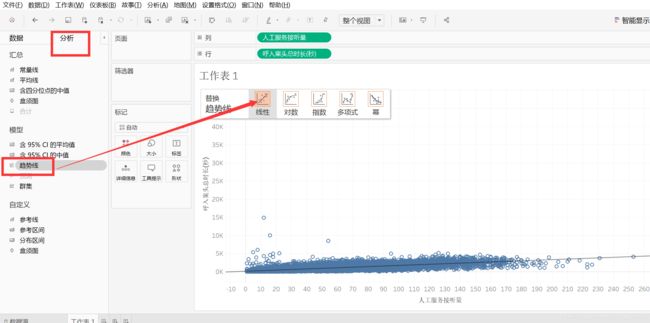
选择【分析】下【模型】里的【趋势线】，拖到右边图表里，会自动显示趋势线选择框，拖到【线性】里。

描述趋势线

右击图表空白处——【描述趋势线】，可见公式和系数。

选择里面的公式，右击复制，然后关闭。

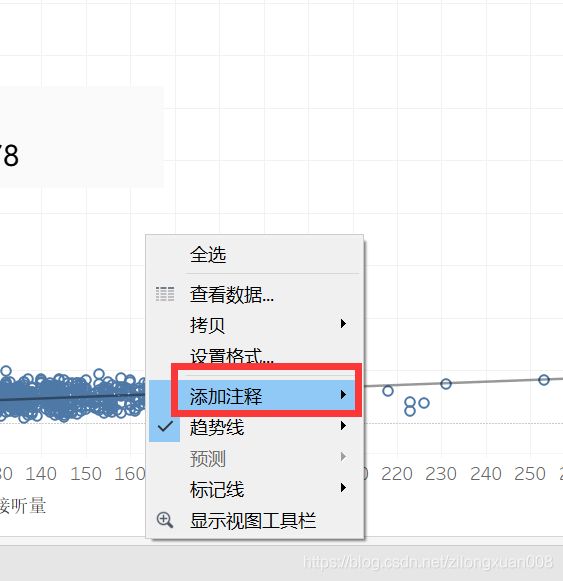
右击图表空白处——【添加注释】——【区域】。

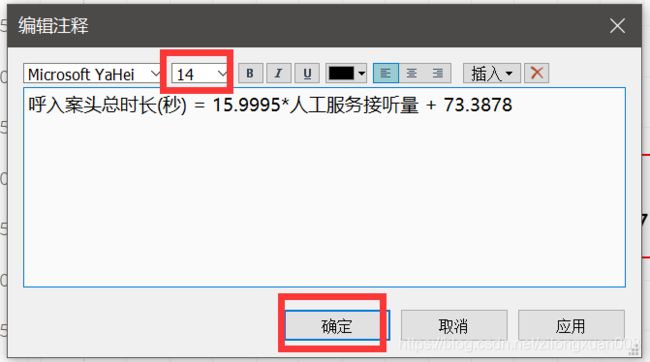
复制公式到里面，选择字号大小，点击【确定】。将注释长宽调整到合适位置。

1.2构建其他回归分析模型

• 对数回归
• 幂回归
• 指数回归
• 多项式回归

对数回归

重命名工作表1为“线性回归”，复制该工作表，重命名为“对数回归”

右击图表空白——【趋势线】——【编辑趋势线】

或者右击图表里的趋势线——【编辑趋势线】。

或者点击趋势线，点击【编辑】。

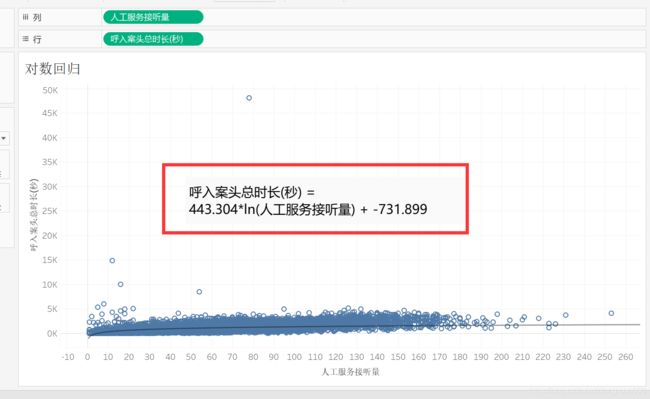
勾选【对数】，选择【确定】。

鼠标悬浮在趋势线上，可见公式，里面的人工服务接听量属于解释变量。

R平方值小于上面的线性，说明不如线性的好。

右击图表空白处——【描述趋势线】，可见公式和系数。

选择里面的公式，右击复制，然后关闭。

双击原来的注释，将公式粘贴进去。

指数回归

复制工作表【对数回归】，重命名为【指数回归】。

点击趋势线，点击【编辑】，勾选【指数】。

鼠标悬浮在趋势线上，可见公式。

R平方值大于上面的对数，说明比对数的好。

右击图表空白处——【描述趋势线】，可见公式和系数。

选择里面的公式，右击复制，然后关闭。

双击原来的注释，将公式粘贴进去。

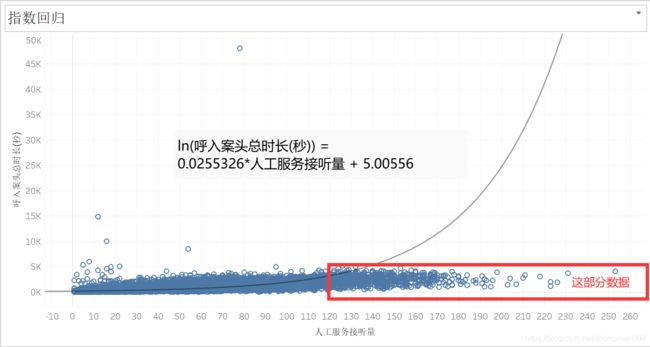
为什么这里的指数回归的R平方值比对数回归的要好？

因为指数回归线下部的数据占比非常少，对拟合结果的影响非常非常小。

比如以人工服务接听量等于120为界限，大于120的为异常数据，创建一个计算字段计算异常数据的占比是多少。

计算字段比较

右击【人工服务接听量】——【创建】——【计算字段】

修改字段名称为【人工服务接听量异常区分】，输入公式IF [人工服务接听量]>120 THEN "异常数据" ELSE "正常数据" END

将【人工服务接听量异常区分】拖入到【颜色】。

新建工作表4。

将【人工服务接听量异常区分】拖到【列】，将【记录数】拖到【行】。

将【记录数】拖到【标签】，右击【总和(记录数)】——【快速表计算】——【合计百分比】。

可见大于120的异常值只占了3.58%，非常少的比例，对拟合优度影响不大。

一般数据分析中，小于6%的数据可以忽略不计。

参数比较

在【指数回归】工作表里，空白处右击——【创建参数】。设置一个参数调整异常数的界定。

参数名称是【人工服务接听量异常定义阈值】，点击【范围】，填入最小值80，最大值180，步长10，点击【确定】。

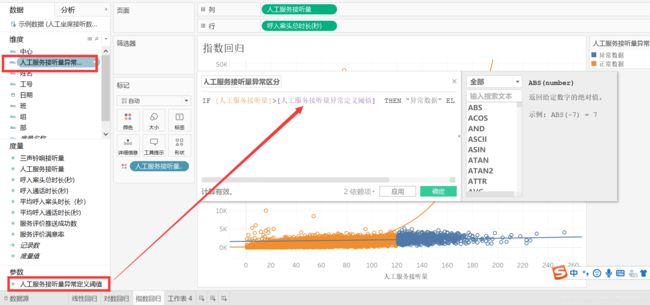
右击【人工服务接听量异常区分】——【编辑】，去除数字120，将【人工服务接听量异常定义阈值】拖入到公式里，点击【确定】。

IF [人工服务接听量]>[人工服务接听量异常定义阈值] THEN "异常数据" ELSE "正常数据" END

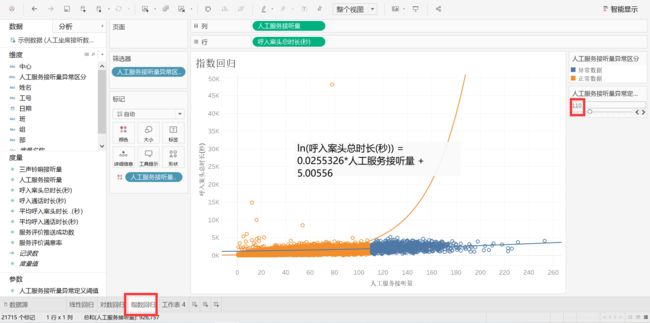
右击【人工服务接听量异常定义阈值】——【显示参数控件】，则右边显示参数控件。

开始值是80。点击【工作表4】，可见比例变化，发现占比不是很大。

在【指数回归】工作表里可以调整参数，在【工作表4】里可以见比例变化。

参考线比较

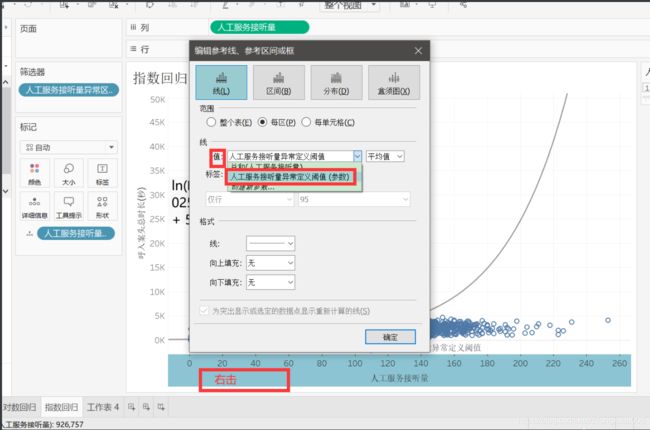
拖走【人工服务接听量异常区分】颜色，将【人工服务接听量异常区分】拖到【详细信息】里。

右击坐标轴空白处——【添加参考线】，【值】选择【人工服务接听量异常定义阈值(参数)】点击确定。

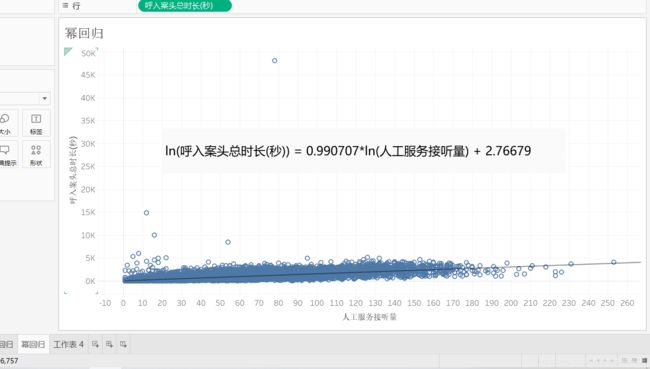
幂回归

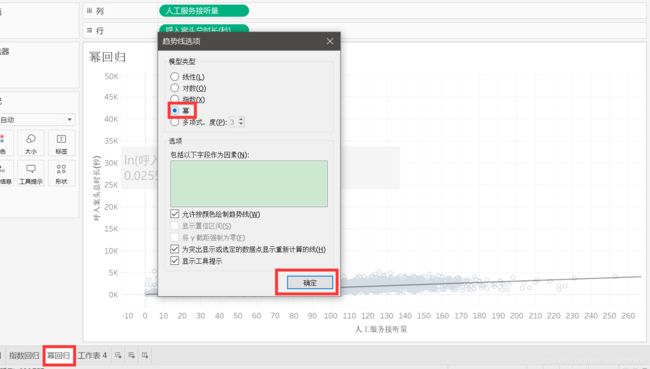
复制【指数回归】工作表，重命名为【幂回归】。

右击趋势线——【编辑趋势线】，选择【幂】，点击【确定】。

鼠标悬浮在趋势线上，可见公式。

R平方值大于以上回归，说明该拟合优度比较好。

P值较小，可以接受。

右击图表空白处——【描述趋势线】，可见公式和系数。

选择里面的公式，右击复制，然后关闭。

双击原来的注释，将公式粘贴进去。

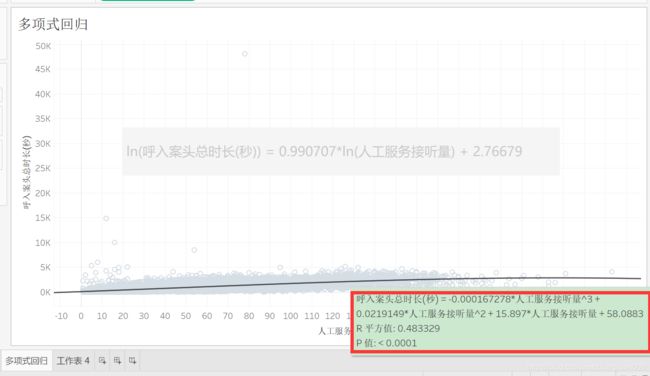
多项式回归

复制【幂回归】工作表，重命名为【多项式回归】。

右击趋势线——【编辑趋势线】，选择【多项式】，【度】的范围是2-8，一般选择3-5，这里选3，点击【确定】。

鼠标悬浮在趋势线上，可见公式。

R平方值一般，说明该拟合优度一般。

P值较小，可以接受。

右击图表空白处——【描述趋势线】，可见公式和系数。

选择里面的公式，右击复制，然后关闭。

双击原来的注释，将公式粘贴进去，字号选择10。

如何评定一个回归分析模型的好坏？

R平方值就是拟合优度，越大越好(在0到1之间)，一般0.4或0.5以上是可以接受的。

P值就是显著性水平，一般设置小于5%，也就是0.05。

2.时间序列分析

时间序列分析预测是对Tableau内嵌周期性数据的一个预测功能。能够自动拟合预测模型，分析数据的变化规律和预测数据，能够对预测模型的参数进行调整，然后评价预测模型的精度。

2.1创建人工服务接听量预测曲线

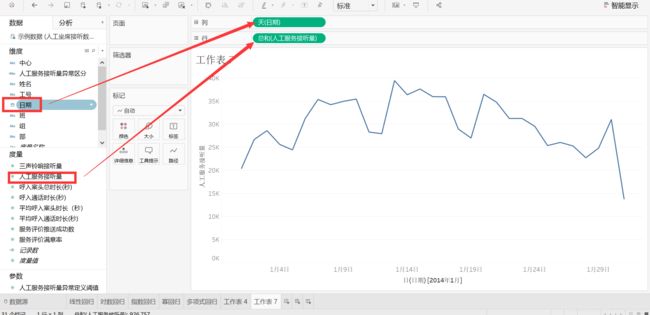
新建工作表7。

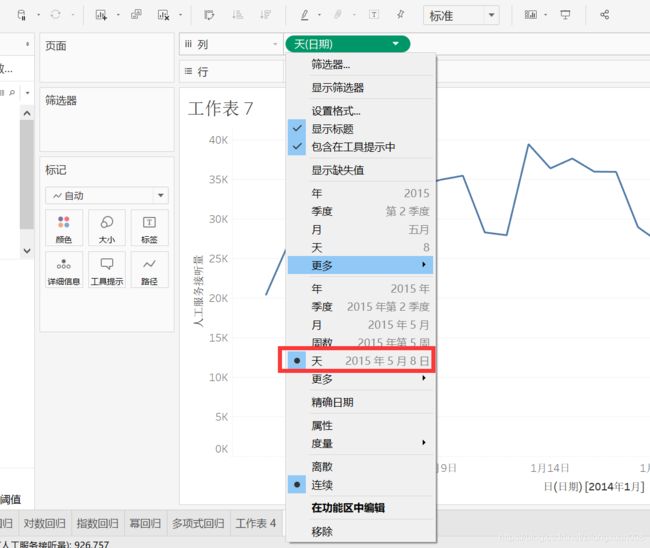
将【人工服务接听量】拖到【行】，将【日期】拖到【列】。

点击【日期】下拉框，选择【天】。

重命名工作表7为【时间序列分析】。

时间序列分析或时间预测本质上是利用原始的时间数据，来拟合出一个模型，研究数据的发展变化的规律，从而得出观测数据的统一特征。找到这个特征，再依据拟合出的模型，外推一个时间段内的数值。

时间序列分析能够识别以周为周期还是以月为周期的匹配情况。

图表的空白处右击——【预测】——【显示预测】。

默认情况下是一条直线，是因为没有进行参数设置。

2.2预测选项设置

图表的空白处右击——【预测】——【预测选项】。

【精确】选择【天】，【直至】选择【9】【天】，【季节】选择【累加】，点击【确定】。

【精确】可以按照天、周、月、季度、年等预测。

【直至】是预测的结束范围。

谨慎注意【用零填充缺少值】，如果缺少值是关键时间点的数值的话，会影响模型，一般会回到原始数据中填写。

【趋势】只有不变、增加或减少三种趋势，没有先增后减，或先减后增等情形。

【季节】就是周期的意思。

【显示预测区间】跟P值有关系，计算方法是1-P=预测区间。

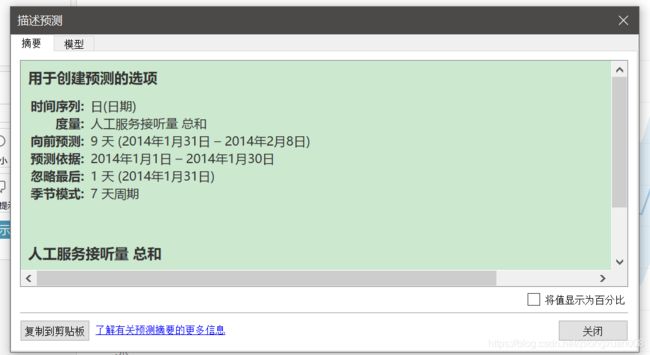
图表的空白处右击——【预测】——【描述预测】。

为什么【忽略最后】要忽略最后一天？是因为最后一天对预测的影响太大，一般会忽略。

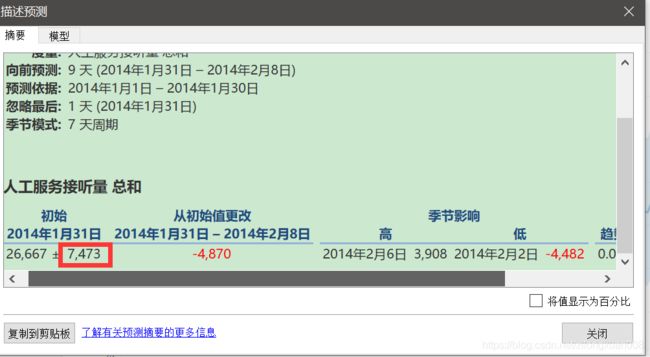
【显示预测区间】是【95%】时，这里的值是7473。

如果【显示预测区间】为【99%】，则值为9821。

恢复【显示预测区间】为【95%】。

质量有三种：差、确定 、好。

将【预测选项】里的【季节】改为【累乘】，在【描述预测】里【质量】显示【确定】。

将【预测选项】里的【趋势】和【季节】都改为【累加】，在【描述预测】里【质量】为【差】。

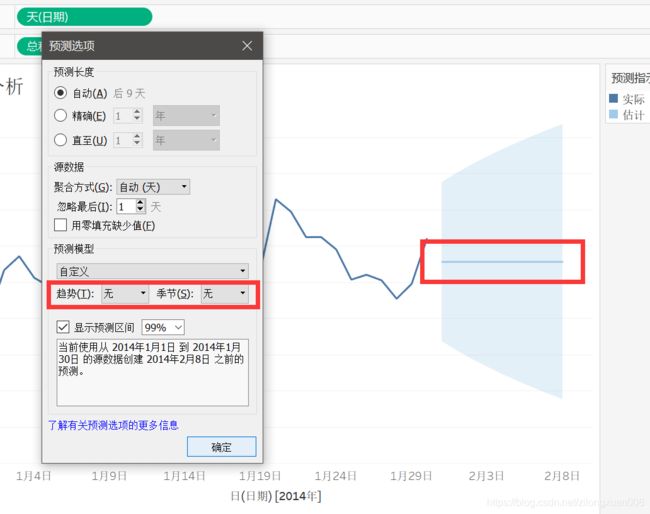
如果将【预测选项】里的【趋势】和【季节】都改为【无】，则预测为直线，说明【趋势】和【季节】都没有做贡献。

累加和累乘的区别

如果数值数量级差异比较大的话，用累乘比较合适。

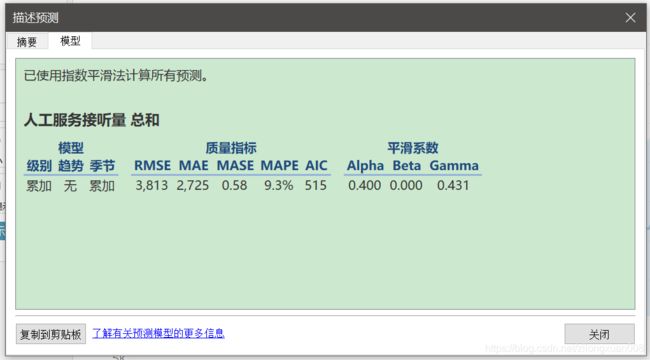
将【预测选项】里的【趋势】改为【无】，【季节】都改为【累加】，打开【描述预测】，可见【模型】。

2.3预测模型评价

【描述预测】里有【质量】。

质量有三种：差、确定 、好。