概率论与数理统计——随机变量及其分布
文章目录
-
-
- 随机变量与分布函数
-
- 1.随机变量
- 2.分布函数
- 3.由分布函数求概率
- 随离散型随机变量及其分布
-
- 1.一维离散型随机变量
- 2.分布律
- 3.离散型随机变量
- 4.重要分布
- 连续型随机变量
-
- 1.连续型随机变量的概率密度
- 2.连续型随机变量的概率密度函数 f ( x ) f(x) f(x)的性质
- 3.连续型随机变量的概率密度与分布函数以及事件概率的关系
- 4.重要分布
- 随机变量函数的分布
-
- 1.离散型随机变量函数的分布
- 2.连续型随机变量函数的分布
-
随机变量与分布函数
1.随机变量
设E是一个随机试验,其样本空间为Ω={ω},如果对于每一个样本点ω∈Ω,都有唯一一个实数X(ω)与之对应,则称X(ω)为一维随机变量,通常用X,Y,Z,···表示随机变量。
通俗来讲,随机变量就是在每次试验结束后我们所关注的与结果有关的变量。(例如:我们在掷骰子时,我们往往可能关注的是每次掷完骰子后两骰子的点数之和,而不会在意具体两枚骰子的点数,像这种“两骰子的点数之和”变量就可以是这个试验的随机变量)
2.分布函数
设X是一个随机变量,x是任意实数,则函数F(x)=P{X≤x}称为X的分布函数
基本性质
(1)单调性:F(x)是一个单调不减的函数,即当x1
F ( + ∞ ) = lim x − > + ∞ F ( x ) = 1 F(+\infty)=\lim_{x->+\infty }F(x)=1 F(+∞)=limx−>+∞F(x)=1 F ( − ∞ ) = lim x − > − ∞ F ( x ) = 0 F(-\infty)=\lim_{x->-\infty }F(x)=0 F(−∞)=limx−>−∞F(x)=0
(3)连续性:F(x+0)=F(x),即F(x)是右连续函数(x+0这里为x处的右极限)
3.由分布函数求概率
P { a < X ≤ b } = P { X ≤ b } − P { X ≤ a } = F ( b ) − F ( a ) P\{a
随离散型随机变量及其分布
1.一维离散型随机变量
若随机变量X的全部可能取值是有限个或可列个(或者该随机变量X的概率1以一定规律分布在各个可能的值上),则称X为离散型随机变量
2.分布律
离散型随机变量X所有可能取值为 x k x_{k} xk( k k k=1,2,···),事件{ x k x_{k} xk}的概率为P{ x k x_{k} xk}= p k p_{k} pk( k k k=1,2,···),则称P{X= x k x_{k} xk}= p k p_{k} pk( k k k=1,2,···)为X的分布律或分布列。
分布律也可以写成表格形式:
| X | x 1 x_{1} x1 x 2 x_{2} x2 ⋅ ⋅ ⋅ ··· ⋅⋅⋅ x k x_{k} xk ⋅ ⋅ ⋅ ··· ⋅⋅⋅ |
|---|---|
| P | p 1 p_{1} p1 p 2 p_{2} p2 ⋅ ⋅ ⋅ ··· ⋅⋅⋅ p k p_{k} pk ⋅ ⋅ ⋅ ··· ⋅⋅⋅ |
离散型随机变量的分布律的性质:
(1)P{X= x k x_{k} xk}= p k p_{k} pk≥0, k k k=1,2,···
(2) ∑ k \sum_{k} ∑kP{X= x k x_{k} xk}= ∑ k p k \sum_{k}p_{k} ∑kpk=1
3.离散型随机变量
(1)如果已知X的分布律为P{X= x k x_{k} xk}= p k p_{k} pk( k k k=1,2,···),则X的分布函数
F ( x ) = P { X ≤ x k } = ∑ x k ≤ x p k F(x)=P\{X≤x_{k}\}=\sum_{x_{k}≤x}p_{k} F(x)=P{X≤xk}=∑xk≤xpk
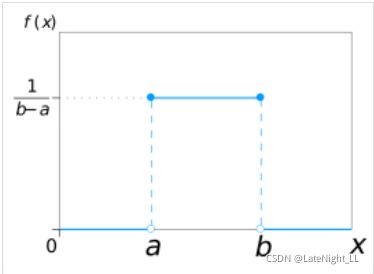
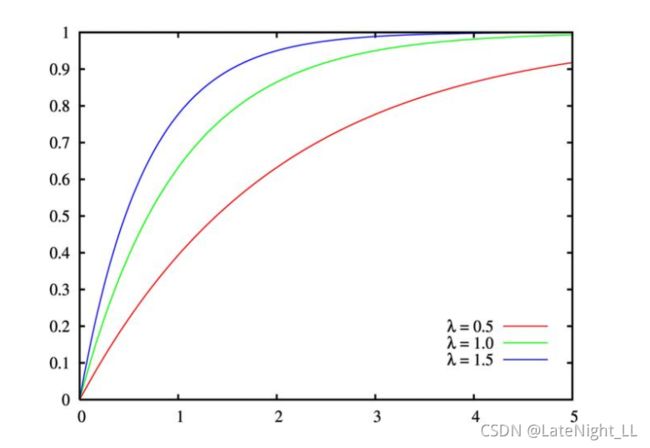
而事件{a P { a < X ≤ b } = ∑ a < x k ≤ b p k P\{a (2)如果已知X的分布函数F(x),则X的分布律为 P{X= x k x_{k} xk}=F( x k x_{k} xk)-F( x k − 0 x_{k}-0 xk−0) (1)(0-1)分布 其分布律为 其中事件A 发生的概率为p,0 (2)二项分布 P { X = k } C n k p k q n − k , k = 0 , 1 , ⋅ ⋅ ⋅ , n P\{X=k\}C_{n}^{k}p^{k}q^{n-k},k=0,1,···,n P{X=k}Cnkpkqn−k,k=0,1,⋅⋅⋅,n 其中p为事件A在每次试验中出现的概率,q=1-p,称随机变量X服从二项分布记作 X X X~ B ( n , p ) B(n,p) B(n,p) 适用于:eg:在n重伯努利试验中事件A发生k次的概率 (3)泊松分布 P { X = k } = λ k e − λ k ! ( k = 1 , 2 , ⋅ ⋅ ⋅ ) P\{X=k\}=\frac{\lambda ^{k}e^{-\lambda}}{k!}(k=1,2,···) P{X=k}=k!λke−λ(k=1,2,⋅⋅⋅) 其中λ>0是常数,则称X服从λ的泊松分布,记为 X X X~ π ( λ ) 或 P ( λ ) π(λ)或P(λ) π(λ)或P(λ) 参数λ是单位时间或单位面积内随机事件的平均发生次数,k为实际发生次数 泊松定理: 设随机变量Xn~B(n,p),若 lim n → ∞ n p n \lim_{n\rightarrow \infty }np_{n} limn→∞npn=λ>0,则有 lim n → ∞ C n i p n i ( 1 − p n ) n − i = λ i i ! e − λ \lim_{n\rightarrow \infty }C^{i}_{n}p^{i}_{n}(1-p_{n})^{n-i}=\frac{λ^{i}}{i!}e^{-λ} limn→∞Cnipni(1−pn)n−i=i!λie−λ 由泊松定理,二项分布可以用泊松分布作为近似。 超几何分布 P { X = i } = C M i C N − M n − i i ! P\{X=i\}=\frac{C^{i}_{M}C_{N-M}^{n-i}}{i!} P{X=i}=i!CMiCN−Mn−i, ( i = 0 , 1 , 2 , ⋅ ⋅ ⋅ , l ; l = m i n { n , m } ) (i=0,1,2,···,l;l=min\{n,m\}) (i=0,1,2,⋅⋅⋅,l;l=min{n,m}) 其中M,N,n都是自然数,且n 适用于:eg:共有N件物品,其中M件是特异,从中取出n件物品,其中有i件是特异的概率 几何分布 P { X = i } = ( 1 − p ) i − 1 p , i = 1 , 2 , ⋅ ⋅ ⋅ P\{X=i\}=(1-p)^{i-1}p,i=1,2,··· P{X=i}=(1−p)i−1p,i=1,2,⋅⋅⋅ 其中0 如果对于随机变量X的分布函数F(x),存在非负可积函数f(x),使得对任意实数x,有 F ( x ) = ∫ − ∞ x f ( t ) d t F(x)=\int_{-\infty }^{x}f(t)dt F(x)=∫−∞xf(t)dt成立,则称X为连续型随机变量,函数f(x)称为X的概率密度(或分布密度)。 (1) f ( x ) ≥ 0 f(x)≥0 f(x)≥0; (2) ∫ − ∞ + ∞ f ( x ) d x = 1 \int_{-\infty}^{+\infty }f(x)dx=1 ∫−∞+∞f(x)dx=1; (1)若X的概率密度为 f ( x ) f(x) f(x),则X的分布函数为 F ( x ) = ∫ − ∞ x f ( t ) d t F(x)=\int_{-\infty}^{x}f(t)dt F(x)=∫−∞xf(t)dt,当 f ( x ) f(x) f(x)为分段函数时其分布函数 F ( x ) F(x) F(x)要做分段讨论; (2)若 f ( x ) f(x) f(x)在点x出连续,则有 F ‘ ( x ) = f ( x ) F`(x)=f(x) F‘(x)=f(x); (3) P { a < X ≤ b } = P { a < X < b } = P { a ≤ X < b } = P { a ≤ X ≤ b } P\{a (4) P { X = a } = 0 ( − ∞ < a < + ∞ ) P\{X=a\}=0(-\infty (1)均匀分布:若连续型随机变量X的概率密度函数为 f ( x ) = { 1 b − a , a ≤ x ≤ b 0 , e l s e f(x)=\left\{\begin{matrix} & \frac{1}{b-a} &,a≤x≤b \\ &0& ,else \end{matrix}\right. f(x)={b−a10,a≤x≤b,else (2)指数分布:若连续型随机变量X的概率密度函数为 f ( x ) = { λ e − λ x , x > 0 0 , e l s e f(x)=\left\{\begin{matrix} & λe^{-λx}&,x>0 \\ &0& ,else \end{matrix}\right. f(x)={λe−λx0,x>0,else (3)正态分布:若连续型随机变量X的概率密度函数为 f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sqrt{2}πσ}e^{-\frac{(x-μ)^{2}}{2σ^{2}}} f(x)=2πσ1e−2σ2(x−μ)2 ( − ∞ < x < + ∞ ) (-∞ 其中μ和σ>0都是常数,则称X服从参数为μ和σ的正态分布,简记为X~N(μ,σ 2 ^{2} 2).(如下图) φ ( x ) = 1 2 π e − x 2 2 φ(x)=\frac{1}{\sqrt{2}π}e^{-\frac{x^{2}}{2}} φ(x)=2π1e−2x2 Φ ( x ) = 1 2 π ∫ − ∞ x e − t 2 2 d t Φ(x)=\frac{1}{\sqrt{2}π}\int_{-\infty }^{x}e^{-\frac{t^{2}}{2}}dt Φ(x)=2π1∫−∞xe−2t2dt 性质一: Φ(-x)=1-Φ(x) 性质二: 当X~N(μ,σ 2 ^{2} 2)时,U= X − μ σ \frac{X-μ}{σ} σX−μ ~N(0,1).即 F ( x ) = Φ ( X − μ σ ) F(x)=Φ(\frac{X-μ}{σ}) F(x)=Φ(σX−μ). 设随机变量X的分布律为 P { X = x k } = p k , k = 1 , 2 , 3 , ⋅ ⋅ ⋅ P\{X=x_{k}\}=p_{k},k=1,2,3,··· P{X=xk}=pk,k=1,2,3,⋅⋅⋅,则当Y=g(X)的所有取值为 y j ( j = 1 , 2 , ⋅ ⋅ ⋅ ) y_{j}(j=1,2,···) yj(j=1,2,⋅⋅⋅)时,随机变量Y有分布律 P { Y = y k } = ∑ g ( x k ) = y j P { X = x k } P\{Y=y_{k}\}=\sum_{g(x_{k})=y_{j}}P\{X=x_{k}\} P{Y=yk}=∑g(xk)=yjP{X=xk} (1)设随机变量X的概率密度函数为 f X ( x ) ( − ∞ < x < + ∞ ) f_{X}(x)(-\infty F Y ( y ) = P { Y ≤ y } = P { g ( x ) ≤ y } = ∫ g ( x ) < y f X ( x ) d x F_{Y}(y)=P\{Y≤y\}=P\{g(x)≤y\}=\int_{g(x) 其概率密度为 f Y ( y ) = F Y ‘ ( y ) f_{Y}(y)=F_{Y}`(y) fY(y)=FY‘(y) (2)设随机变量X具有概率密度函数 f X ( x ) ( − ∞ < x < + ∞ ) f_{X}(x)(-\infty f Y ( y ) = { f X [ h ( y ) ] ∣ h ‘ ( y ) ∣ , α < y < β 0 , e l s e f_{Y}(y)=\left\{\begin{matrix} f_{X}[h(y)]|h`(y)|&,α 其中h(y)是g(x)的反函数,α=min{g(-∞),g(+∞)},β=max{g(-∞),g(+∞)}
(ps:xk-0这里为xk处的左极限,可以理解为xk减去了一个无穷小)
4.重要分布
X
1 0
P
p 1-p
设在n重伯努利试验中事件A发生的次数为X,则
设随机变量X的分布律为:
适用于:eg:单位时间内事件的平均发生次数λ,事件实际发生k次的概率
设随机变量X的分布列是
设随机变量X的分布列为
连续型随机变量
1.连续型随机变量的概率密度
2.连续型随机变量的概率密度函数 f ( x ) f(x) f(x)的性质
3.连续型随机变量的概率密度与分布函数以及事件概率的关系
4.重要分布

(4)标准正态分布
对于正态分布,当μ=0、σ=1时称X服从标准正态分布,简记为X~N(0,1),其概率密度函数和分布函数分别用φ(x),Φ(x)表示,即有
随机变量函数的分布
1.离散型随机变量函数的分布
2.连续型随机变量函数的分布