python图像处理：图像的傅里叶变换、低通滤波、高通滤波、带通滤波

原理

大家都知道，在一维上，傅里叶变换：

1. 能将一个时域上的信号转换到频率域上
2. 认为一个周期信号能用若干三角函数的和来表示

在二维上，我们也可以将图片看做信号，只不过这个信号是在空间域上的。
我们在观察时域上的信号变化时，是根据某个时间点的信号幅度与其相邻时间点的信号幅度来判断，同理，在空间域上，是根据某个空间点(比如的2行3列的像素点）信号幅度与其相邻空间点的信号幅度来判断其变化的，但与一维相比，二维多了方向这个概念。

二维傅里叶变换：

1. 能将一个空间域上的信号转换到频率域上
2. 认为一个周期信号能用若干三角函数的和来表示

问题来了，二维的三角函数是什么样子？

大家可以想象水面上泛起的涟漪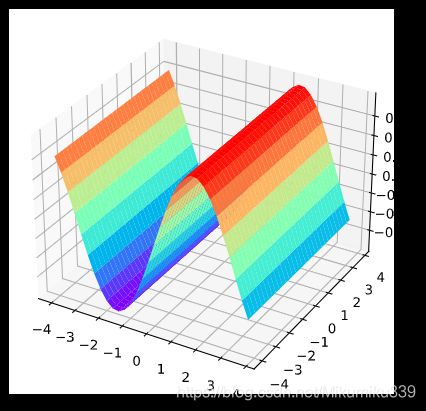
我们为了能让其用图片表示，就让这个三角函数的值等于图片对应像素的灰度值，于是得到下面的图片：

当然，条纹有疏有密，有以各种角度倾斜的，有各种各样条纹才能组成含义丰富的图片。

所以，不难理解

二维傅里叶变换认为一个周期信号能用若干三角函数的和来表示

即

二维傅里叶变换认为一个张图能用若干条纹的和来表示

有了这个概念，也就不难理解图片的频率了。

请想象一张草原上奔跑着几只斑马的图片：

一张图片中的低频信号，就是那些由稀疏条纹组成的，比如说图片里的大草原，草原是一片绿色，信号变化的很慢。
一张图片中的高频信号，就是那些由密集条纹组成的，比如说图片里的斑马，还有一些边缘信息，信号变化的很快。

低通滤波，就是低频率的信号能通过；高通滤波，就是高频率的信号能通过；带通滤波，就是选定频率的信号能通过。

二维傅里叶变换的公式表示：

M，N分别是一张图片的行、列；u，v分别是水平频率与竖直频率。
条纹的方向与(u/M,v/N)平行，条纹的数量与u+v成正比。

参考链接1
参考链接2(推荐)

应用

去网纹

实践

带通的频率选择随需求改变，但原理与低通高通一样，就不再展示。

代码：

import numpy as np
import matplotlib 
import matplotlib.pyplot as plt 
matplotlib.rcParams['font.family'] = 'simHei'
matplotlib.rcParams['axes.unicode_minus'] = False
%matplotlib qt5
import cv2
import math
img = cv2.imread('apple.png')
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
f = np.fft.fft2(img_gray)
#shift 将低频移到中间 
fshift = np.fft.fftshift(f)
rows,cols = fshift.shape
mid_x,mid_y = int((rows)/2),(int((cols)/2))
#高通
mask1 = np.ones((rows,cols),dtype=np.uint8)
mask1[mid_x-5:mid_x+5,mid_y-5:mid_y+5] = 0
fshift1 = mask1*fshift
isshift1 = np.fft.ifftshift(fshift1)

#低通蒙板
mask2 = np.zeros((rows,cols),dtype=np.uint8)
mask2[mid_x-10:mid_x+10,mid_y-10:mid_y+10] = 1
fshift2 = mask2*fshift
isshift2 = np.fft.ifftshift(fshift2)

high = np.fft.ifft2(isshift1)
low = np.fft.ifft2(isshift2)

img_high = np.abs(high)
img_low = np.abs(low)

#展示
fshift1[fshift1==0j] = 1
fshift1 = np.log(np.abs(fshift1))
fshift2[fshift2==0j] = 1
fshift2 = np.log(np.abs(fshift2))

plt.subplot(321)
plt.imshow(img_gray,'gray')
plt.title('原图')
plt.subplot(322)
plt.imshow(np.log(np.abs(f)),'gray')
plt.title('原始fft')
plt.subplot(323)
plt.imshow(img_high,'gray')
plt.title('高通')
plt.subplot(324)
plt.imshow(fshift1,'gray')
plt.title('高通fft')
plt.subplot(325)
plt.imshow(img_low,'gray')
plt.title('低通')
plt.subplot(326)
plt.imshow(fshift2,'gray')
plt.title('低通fft')
plt.show()