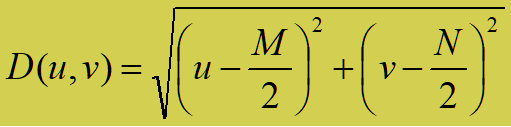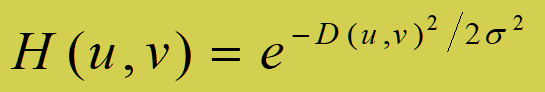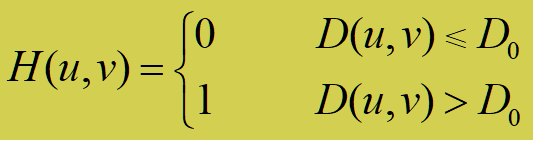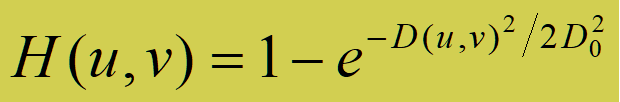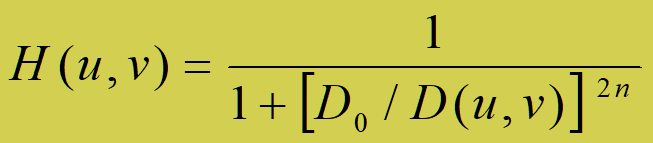数字图像处理频域滤波实现低通与高通滤波（包含matlab代码）

低通滤波器

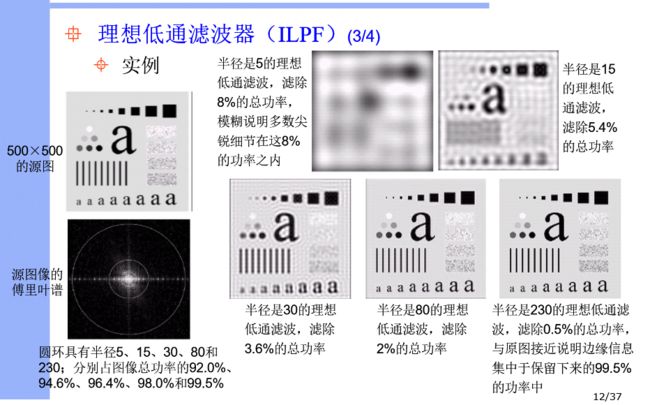
理想低通滤波

• 作用：保留频谱图中圆内低频分量，截断频谱图中圆外高频分量
• 函数表示：

• 假设频谱中心在 (M/2,N/2)处，则任意频谱成分(u,v) 到中心（原点）的距离D(u,v) 定义为：

• D0为低通滤波器截止频率

• 图像表示：

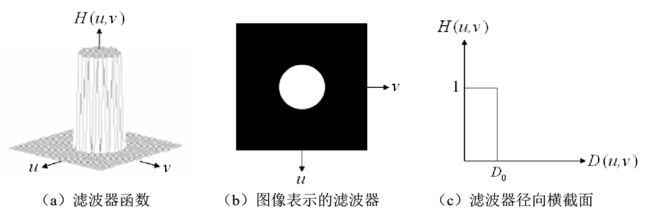
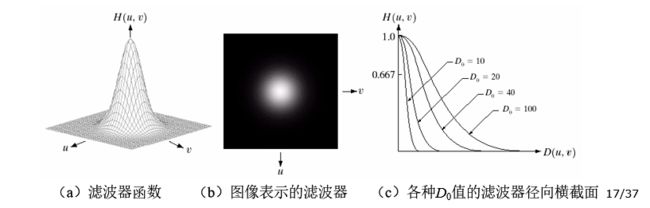
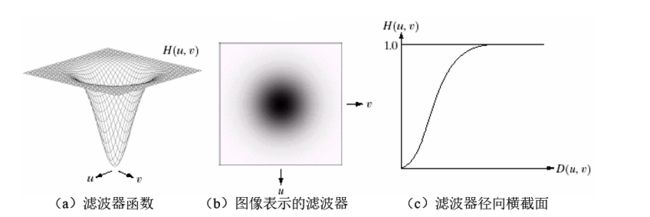
• 从左到右分别是一个理想低通滤波器变换函数的透视图、以图像形式显示的滤波器和滤波器径向横截面。

  

• 说明：在半径为D0的圆内，所有频率没有衰减地通过滤波器，而在此半径的圆之外的所有频率完全被衰减掉

• matlab代码：

%理想低通
I = imread('aaa.tif');
figure(1);
subplot(221),imshow(I);
title('原图像');
I=im2double(I);
s=fftshift(fft2(I));%傅里叶变换，直流分量搬移到频谱中心
subplot(222), imshow(log(abs(s)+1),[]); 
title('图像傅里叶变换取对数所得频谱');
[a,b]=size(s);
h=zeros(a,b);%滤波器函数
res=zeros(a,b);%保存结果
a0=round(a/2);
b0=round(b/2);
d=40;
for i=1:a 
    for j=1:b 
        distance=sqrt((i-a0)^2+(j-b0)^2);
        if distance<=d
            h(i,j)=1;
        else
            h(i,j)=0;
        end
    end
end
res=s.*h;
res=real(ifft2(ifftshift(res)));
subplot(223),imshow(res);
title('理想低通滤波所得图像'); 
subplot(224),imshow(h);
title("理想低通滤波器图象");

• 运行结果：

  

高斯低通滤波

• 二维高斯低通滤波器定义如下：

  

• 是关于频谱中心的扩展度的度量

• 令 =D0，则二维高斯低通滤波器表示为：

• D0为截止频率距原点的距离，D(u,v)是点(u,v)距原点的距离

• 图像表示：

  从左到右分别是一个理想低通滤波器变换函数的透视图、以图像形式显示的滤波器和滤波器径向横截面。

  

• matlab代码：

%高斯低通
I=imread('aaa.tif');
subplot(221),imshow(I);
title('原图像');
Y=fft2(im2double(I));%傅里叶变换
Y=fftshift(Y);%频谱搬移,直流分量搬移到频谱中心
subplot(222), imshow(log(abs(Y)+1),[]); 
title('图像傅里叶变换取对数所得频谱');
[M,N]=size(Y);%获得图像的高度和宽度
h=zeros(M,N);%滤波器函数
%图像中心点
M0=M/2;
N0=N/2;
%截至频率距离圆点的距离，delta表示高斯曲线的扩散程度
D0=40;
delta=D0;
for x=1:M
    for y=1:N
        %计算点（x,y）到中心点的距离
        d2=(x-M0)^2+(y-N0)^2;
        %计算高斯滤波器
        h(x,y)=exp(-d2/(2*delta^2));
    end
end
%滤波后结果
res=h.*Y;
res=real(ifft2(ifftshift(res)));
subplot(223),imshow(res);
title('高斯低通滤波所得图像'); 
subplot(224),imshow(h);
title("高斯低通滤波器图象");

• 运行结果：

  

巴特沃斯低通滤波

• n阶巴特沃思低通滤波器定义如下：

  

• D0为截止频率与原点的距离，D(u,v)是点(u,v)与原点的距离

• 图像表示：

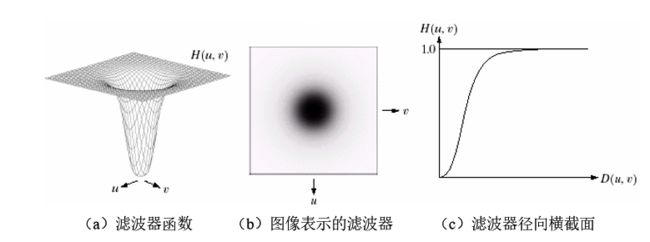
• 不同于ILPF，BLPF在通带与被滤除的频率之间没有明显的截断

• 当D(u,v)=D0时，H(u,v)=0.5；当D(u,v)=0时，滤波器取最大值1

• 巴特沃斯滤波器阶数越高，越趋近于理想低通滤波器

• matlab代码：

%巴特沃斯低通
figure(3);
I=imread('aaa.tif');
subplot(221),imshow(I);
title('原始图像');
Y=fft2(im2double(I));%傅里叶变换
Y=fftshift(Y);%频谱搬移,直流分量搬移到频谱中心
subplot(222), imshow(log(abs(Y)+1),[]); 
title('图像傅里叶变换取对数所得频谱');
[M,N]=size(Y);%获得图像的高度和宽度
h=zeros(M,N);%滤波器函数
%图像中心点
M0=M/2;
N0=N/2;
d0=40;
%巴特沃斯滤波器的阶数
n_0=2;
for x=1:M
    for y=1:N
        distance=sqrt((x-M0)^2+(y-N0)^2);
        h(x,y)=1/(1+(distance/d0)^(2*n_0));
    end
end
%滤波后结果
res=h.*Y;
res=real(ifft2(ifftshift(res)));
subplot(223),imshow(res);
title('巴特沃斯低通滤波所得图像'); 
subplot(224),imshow(h);
title("巴特沃斯低通滤波器图象");

• 运行结果：

  

低通滤波器用途

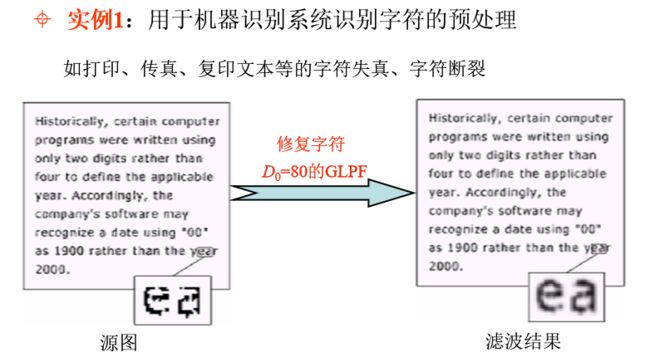
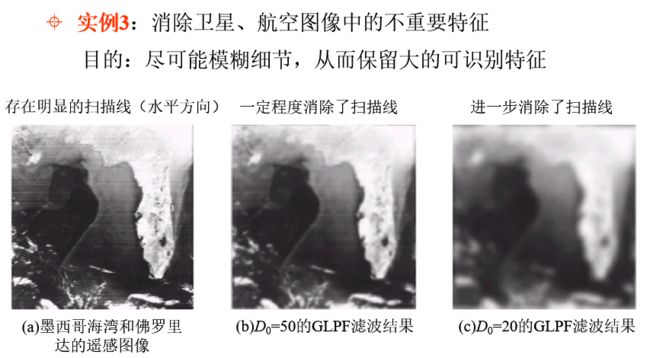
• 低通滤波器的应用实例：模糊、平滑等

  • 字符识别：通过模糊图像，桥接断裂字符的裂缝

    

  • 印刷和出版业：从一幅尖锐的原始图像产生平滑、柔和的外观，如人脸，减少皮肤细纹的锐化程度和小斑点

    

  • 处理卫星和航空图像：尽可能模糊细节，从而保留大的可识别特征（低通滤波通过消除不重要的特征来简化感兴趣特征的分析）

    

高通滤波

理想高通滤波

• 作用：保留频谱图中圆外高频分量，截断频谱图中圆内低频分量

• 截止频率距原点的距离为 D0 的 IHPF 定义为：

  

• D0为截止频率距原点的距离，D(u,v)是点(u,v)距原点的距离

• 图像表示：

  

• matlab代码：

%理想高通
I = imread('aaa.tif');
figure(1);
subplot(221),imshow(I);
title('原图像');
I=im2double(I);
s=fftshift(fft2(I));%傅里叶变换，直流分量搬移到频谱中心
subplot(222), imshow(log(abs(s)+1),[]); 
title('图像傅里叶变换取对数所得频谱');
[a,b]=size(s);
h=zeros(a,b);%滤波器函数
res=zeros(a,b);%保存结果
a0=round(a/2);
b0=round(b/2);
d=40;
for i=1:a 
    for j=1:b 
        distance=sqrt((i-a0)^2+(j-b0)^2);
        if distance

• 

高斯高通滤波

• 截止频率距原点的距离原点为D0的 GHPF 定义为：

  

• D0为截止频率距原点的距离，D(u,v)是点(u,v)距原点的距离

• 图象表示：

  

• matlab代码：

%高斯高通
I=imread('aaa.tif');
subplot(221),imshow(I);
title('原图像');
Y=fft2(im2double(I));%傅里叶变换
Y=fftshift(Y);%频谱搬移,直流分量搬移到频谱中心
subplot(222), imshow(log(abs(Y)+1),[]); 
title('图像傅里叶变换取对数所得频谱');
[M,N]=size(Y);%获得图像的高度和宽度
h=zeros(M,N);%滤波器函数
%图像中心点
M0=M/2;
N0=N/2;
%截至频率距离圆点的距离，delta表示高斯曲线的扩散程度
D0=40;
delta=D0;
for x=1:M
    for y=1:N
        %计算点（x,y）到中心点的距离
        d2=(x-M0)^2+(y-N0)^2;
        %计算高斯滤波器
        h(x,y)=1-exp(-d2/(2*delta^2));
    end
end
%滤波后结果
res=h.*Y;
res=real(ifft2(ifftshift(res)));
subplot(223),imshow(res);
title('高斯高通滤波所得图像'); 
subplot(224),imshow(h);
title("高斯高通滤波器图象");

• 运行结果

巴特沃斯高通滤波

• n阶且截止频率距原点的距离为 D0 的 BHPF 定义为：

  

• D0为截止频率距原点的距离，D(u,v)是点(u,v)距原点的距离

• 函数图像表示：

• matlab代码：

%巴特沃斯高通
figure(3);
I=imread('aaa.tif');
subplot(221),imshow(I);
title('原始图像');
Y=fft2(im2double(I));%傅里叶变换
Y=fftshift(Y);%频谱搬移,直流分量搬移到频谱中心
subplot(222), imshow(log(abs(Y)+1),[]); 
title('图像傅里叶变换取对数所得频谱');
[M,N]=size(Y);%获得图像的高度和宽度
h=zeros(M,N);%滤波器函数
%图像中心点
M0=M/2;
N0=N/2;
d0=40;
%巴特沃斯滤波器的阶数
n_0=2;
for x=1:M
    for y=1:N
        distance=sqrt((x-M0)^2+(y-N0)^2);
        h(x,y)=1/(1+(d0/distance)^(2*n_0));
    end
end
%滤波后结果
res=h.*Y;
res=real(ifft2(ifftshift(res)));
subplot(223),imshow(res);
title('巴特沃斯高通滤波所得图像'); 
subplot(224),imshow(h);
title("巴特沃斯高通滤波器图象");

• 运行结果：

高通滤波器与低通滤波器之间的关系

• 高通滤波器与低通滤波器的关系

  

• HLP(u,v) ：低通滤波器函数

• HHP(u,v)：高通滤波器函数

• 

• 结论：被低通滤波器衰减的频率成分能通过高通滤波器，反之亦然

高通滤波器与低通滤波器总结比较

低通滤波器

低通滤波器	性能比较
理想低通滤波器	理想低通滤波器产生模糊和振铃现象，且模糊和振铃现象反比于截断频率（即半径D0）
巴特沃斯低通滤波器	随着滤波器半径（截止频率）的增大，模糊越来越减弱；低阶滤波器没有明显振铃现象（滤波器在低频和高频之间平滑过渡）
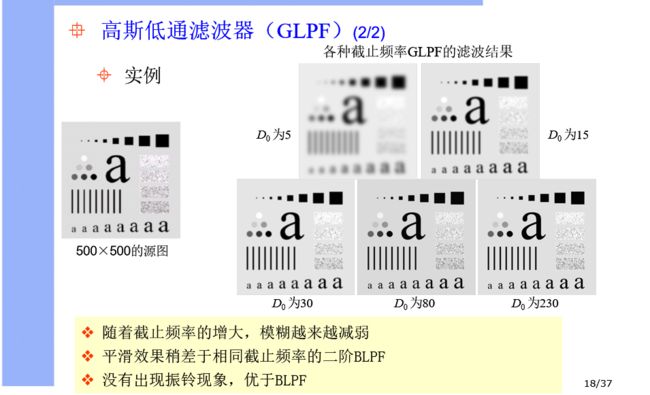
高斯低通滤波器	随着截止频率的增大，模糊越来越减弱；平滑效果稍差于相同截止频率的二阶BLPF；没有出现振铃现象，优于BLPF

理想低通滤波器

巴特沃斯低通

高斯低通

高通滤波器

高通滤波器	性能比较
理想高通滤波器	振铃现象明显
巴特沃斯高通滤波器	BHPF 的结果比 IHPF 的结果尖锐得多，边缘失真也小得多
高斯高通滤波器	GHPF 的结果比 BHBF 和 IHPF 的结果更尖锐，即使是对微小物体 ; 和细线条的滤波也是较清晰的

理想高通滤波器

巴特沃斯高通滤波器

高斯高通滤波器