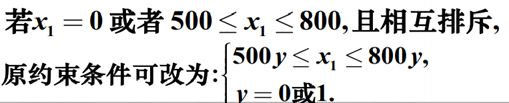Matlab小结6（线性规划）

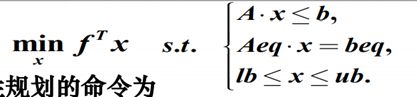
[x,fval] = linprog(f,A,b)
[x,fval] = linprog(f,A,b,Aeq,beq)
[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
x 返回的是决策向量的取值; fval 返回的是目标函数的最优值; f 为价值向量; A,b 对应的是线性不等式约束; Aeq,beq对应的是线性等式约束; lb 对应的是决策向量的下界; ub 对应的是决策向量的上界.
Linprog中无约束则用[]代替，ub无可省略，也可写ub=[inf;inf;inf]
切记标准模型为目标求最小、约束是小于等于，约束大于等于需要变号，目标求最大的表达式要加负号，得到的结果也要加负号

可以转化为线性规划的问题类一


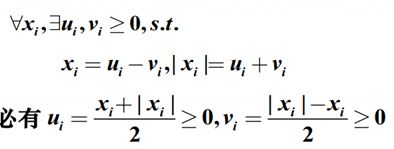
例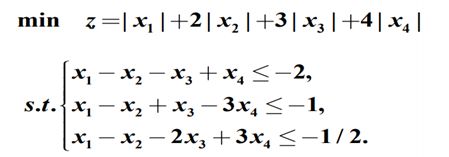

c=1:4;
c=[c,c]‘;
a=[1,-1,-1,1; 1,-1,1,-3;1,-1,-2,3];
a=[a,-a];
b=[-2,-1,-1/2]’;
[y,z]=linprog(c,a,b,[],[],zeros(8,1))
x=y(1:4)-y(5:8) %变换到原问题的解, x=u-v

可以转化为线性规划的问题类二

解法

*对于多目标的问题，处理方法是化成单目标优化
如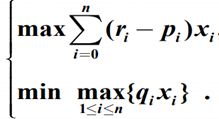
，上面为收益下面为风险，需要对模型简化，固定其中一个，如固定风险，优化收益，设置一个风险值，将下面的式子（风险值和）变为约束条件，反之亦然；或者添加偏好系数s(0<=s<=1) 来定义权重，一个系数s，另一个(1-s)，目标函数minz=sx-(1-s)y，y为求最大的那个；再或者固定一个后，求出其最优解，再将最优解作为约束条件反求另一个，如/固定风险求最大收益模型/得出收益为p，再在/固定收益求最小风险模型/中添加条件收益>=p

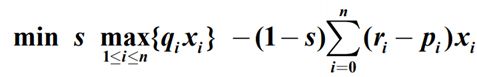
运输模型

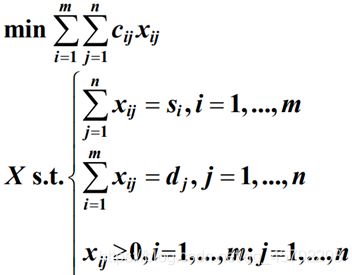
求解函数
function [x,fval,exitflag]=transport_linprog(C,s,d,intkey)
[m,n]=size ( C ) ;X=zeros(nm,m);Y=zeros(nm,n);
for i=0:m-1
X(i*(n+nm)+1:i(n+nm)+n)=1; %依列,隔nm个取n个1
end
for k=1:nm+1:nmn %隔(nm+1)个取值，共取n个
i=0:m-1;
Y(k+ni)=1;
end
Aeq=[X Y].';xm=zeros(1,nm);C1=C.‘;f=C1( : );
Beq=[s( : );d( : )];
if nargin==3
[x,fval,exitflag]=linprog(f,[],[],Aeq,Beq,xm);
else
[x,fval,exitflag]=intlinprog(f,1:(n*m),[],[],Aeq,Beq,xm);
x=round(x);
end
x=reshape(x,n,m).’;
end
例

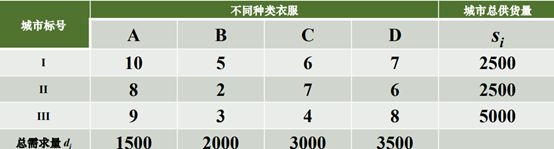
C=[10,5,6,7;8,2,7,6;9,3,4,8]
s=[2500,2500,5000]
d=[1500,2000,3000,3500]
[x,fval,exitflag]=transport_linprog(-C,s,d)
f=-fval
其中exitflag=1表示迭代成功，transport_linprog对于的标准模型求最小，该题求最大，故要乘负号，C变负，同时结果也取负

整数规划
数学规划中的变量（部分或全部）限制为整数时，称为整数规划。若在线性规划模型中，变量限制为整数，则称为整数线性规划。目前所流行的求解整数规划的方法，往往只适用于整数线性规划。目前还没有一种方法能有效地求解一切整数规划。
变量全限制为整数时，称纯（完全）整数规划;变量部分限制为整数的，称混合整数规划。

0-1型整数规划包含：相互排斥的约束条件，固定费用和指派

1. 相互排斥的约束条件
   
   
   也可以不引入M
   或
   类似形式

2. 固定费用
   例
   

3.指派

对于选课问题，要选甲(x1)必选乙(x2)可用x1<=x2描述，x是0-1变量

蒙特卡洛法（随机取样法）
适用于求不规则图形面积和非线性整数规划
不规则图形
例
取不规则图形的上下左右极限，随机取点
x=unifrnd(0,12,[1,10000000]);
y=unifrnd(0,9,[1,10000000]);
pinshu=sum(y=3);
area_appr =129pinshu/10^7

非线性整数规划
例
枚举试探法，需要100^5个点
p0=0;rand(‘state’,sum(clock)); %
tic
for i=1:10^6
x=randi([0,99],1,5);
[f,g]=mengte(x);
if all(g<=0)
if p0 x0=x; p0=f;
end
end
end
x0,p0
toc
其中外置函数为
function [f,g]=mengte(x);
f = x(1)^ 2+x(2)^ 2+3x(3)^ 2+4x(4)^2+2x(5)-8x(1)-2x(2)-3x(3)-x(4)-2x(5);
g = [sum(x)-400
x(1)+2x(2)+2x(3)+x(4)+6x(5)-800
2x(1)+x(2)+6x(3)-200
x(3)+x(4)+5*x(5)-200];

求解混合整数线性规划的函数是 intlinprog
[x,fval]=intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)
其中, intcon表示取整约束变量填变量的序号就行，A和Aeq为矩阵，其余全为列向量
对于模型

例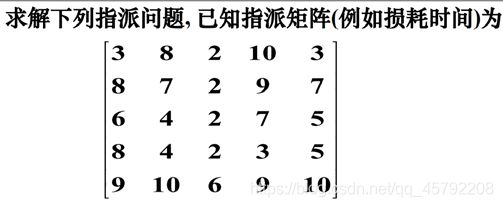
clc, clear,close all
c=[3 8 2 10 3
8 7 2 9 7
6 4 2 7 5
8 4 2 3 5
9 10 6 9 10];
c=c( : ); a=zeros(10,25); intcon=1:25;
for i=1:5
a(i,(i-1)5+1:5i)=1;
a(5+i,i:5:25)=1;
end
b=ones(10,1); lb=zeros(25,1); ub=ones(25,1);
x=intlinprog(c,intcon,[],[],a,b,lb,ub);
x=reshape(x,[5,5])
这题体现了指派和线性规划的相互转化，代码有很多容易误解的地方，c=c(:)是将c按列取变成一列，a(i,(i-1)5+1:5i)=1的后半部分是第(i-1)5+1列到第5i列，因为没加括号很容易误解，a(5+i,i:5:25)=1的后面部分就是i到25间隔5，reshape也是按列取，再按列排

线性规划和运输模型的区别联系
运输模型的实质其实是线性规划，全是等号的运输模型可以用linprog中的Aeq代替，但如果这样，Aeq的的行数代表约束条件个数，每一行的列数都是变量数量mn个，矩阵有（约束条件数m*n）个元素非常庞大，所以提出transport_linprog简化输入过程和运算，只需要输入表的矩阵即可。