【pytorch】（deeplizard22-26）加载数据 | 训练模型 | 计算梯度 | 优化

p22 将一个图像传递到网络中并输出预测

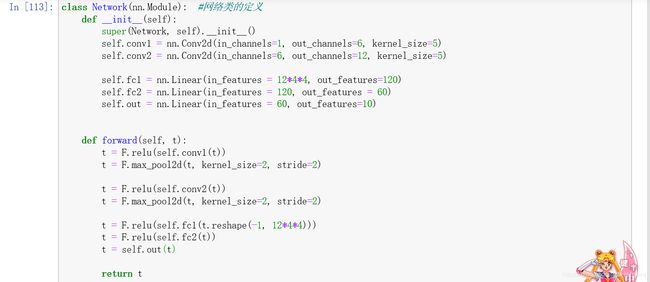
理解前向传播：将输入张量转换为输出张量的过程

将前面的一系列整合：

在开始之前，要关闭pytorch的梯度计算特性，这将阻止pytorch通过网络将张量构建成一个计算图。这个计算图通过跟踪张量在网络中传播的每一个计算来跟踪网络的映射，然后在训练过程中使用这个图形来计算导数（损失函数的导数），在训练模型的时候才打开。

预测的张量形状是[1,10]，第一个轴长度是1，第二个轴长度是10：即在批处理中有一个图像和10个预测类。第一个图像的标签是9，使用Argmax函数，可以看到我们的预测张量中，最高的值也出现在以指数表示的类中。

如果想要这些预测的值成为概率，则可以使用softmax函数（nn.functional包）如下：

不同的网络中，我们得到的预测是不同的，因为权值不同

p23 将一批图像传递到网络中并输出

一批数据，利用数据加载器来获得批处理

通过访问Fashon-mnist类，在torchvision和数据集的内部来创建我们的训练集

 

然后从数据加载器中取出一批数据，然后在从批处理中解压缩图像和标签张量

调用next（iter（））数据加载器会返回一批十张图片

下一步：将图像张量传递给网络得到一个预测

可以看到，预测张量的形状是10*10：即我们有10张图片，对这10张图片，我们有10个预测类；每一个数组元素都包含了对应图像的每个类别的10个预测（就是一个概率），里面的每个预测就是每个值，都是特定输出类的赋值

 

我们使用argmax函数来看概率最大的那个，就知道是哪个类别了（输出索引）

argmax函数的记过是一个10个预测类别的张量，每个数字都是最高值的索引

 

将输出的最大值和标签张量进行对比，用eq（）函数

如果argmax输出中的预测类别与标签匹配，就是ture，否则为false

也就是([3, 3, 3, 3, 3, 3, 3, 3, 3, 3])与([9, 0, 0, 3, 0, 2, 7, 2, 5, 5])依次进行对比

然后调用sum就知道正确的预测数是多少，可以包装成一个get_mum_correct函数

p24 输入张量在通过网络的时候是如何变化的

cnn输出大小的公式：O = [（n-f+2p）/s] + 1

n：一个n*n正方形的输入   f：一个f*f正方形的滤波器

p：paddig边框（填充）     s：移动的步数

 

 

以下是output shape变化的过程：

identity function        torch.size([1,1,28,28])

convolution(5*5)        [1,6,28,28]

Max pooling(2*2)        [1,6,12,12]

convolution(5*5)        [1,12,8,8]

Max pooling(2*2)        [1,12,4,4]

Flatten(reshape)         [1,192]

Linear transformation    [1,120]

Linear transformation    [1,120]

Linear transformation    [1,10]

一开始是28*28的图，传入第一层（5*5的滤波器），则n=28，f=5，无填充，所以p=0，s=1，所以得到24

然后下一步n=24，f=2（2*2的滤波器），此时步长s=2，所以得到O=12

依次这样往下计算，就得到了4*4，即maxpooling（2*2）时，shape为[1,12,4,4]

 

接着要把高度和宽度分开，当不是正方形的时候，分别有针对高度h和针对宽度w的公式（公式是一样的，带入数据不同）

 

P25 训练卷积神经网络

3、训练网络

训练神经网络7个步骤：

1 从训练集得到一批数据

2 把数据传递给网络

3 计算损失（网络返回的预测值与真实值之间的差异）【用一个损失函数来执行】

4 计算损失函数的梯度和网络的权值【用一个反向传播来执行】

5 更新权值，使用梯度来减少损失【用一个优化算法来执行】

6 重复步骤1~5，直到一个周期完成

7 重复步骤1~6，已获得所期望的精确度

 

epoch来表示我们整个训练集的时间周期

 

以上是之前学过的内容，以下是训练网络的内容

3 首先计算损失：

将图像传入网络，得到预测pred，然后从pytorch功能API内部获取交叉熵损失函数，cross_entropy将计算我们的损失并返回一个张量，然后调用item（）来得到损失的数值；

交叉熵函数来自于之前导入的nn.functional接口；

4计算梯度：

已经有了损失，下一步就是计算梯度，会在损失张量上调用反向函数

首先检查第一个卷积层上的梯度值，然后在最后一个张量上运行一个反向函数

这个梯度张量和权重张量有相同的形状，对于权重张量的每一个参数都有一个对应的梯度

当我们在最后一个张量上调用反向传播时，图中的每个张量的梯度都可以计算出来

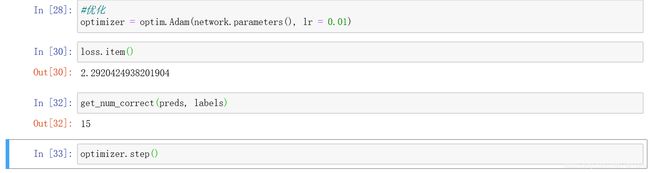
5 优化

优化我们使用SGD或者adam

首先要将网络的参数传递给构造函数，Adam中第二个参数是学习率（LR）

第一个语句就是创建优化器optimizer，然后是再次检查损失，然后价差正确的预测数，下一步step就是告诉优化器想要在损失函数最小方向上优化，于是网络权重得到更新

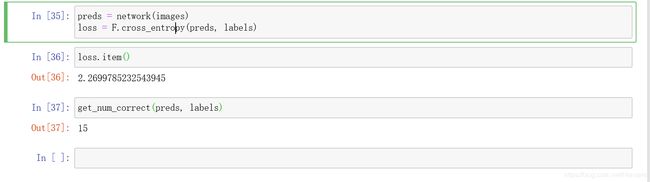
然后再次将相同的一批图像传递到网络中，得到新的损失

于是预测和损失都得到了更新

整体看第三步：小循环

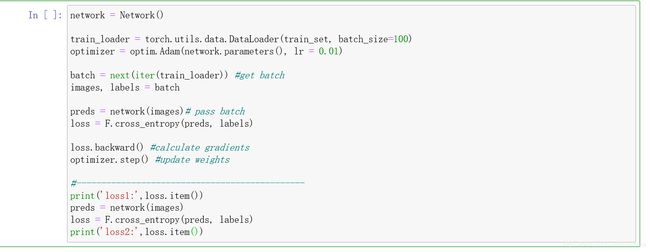
下一步整体看下刚刚的所有东西

创建网络 à 数据加载器加载数据、定义优化器 à 加载数据，解压成图像和标签 à 将图像传递给网络得到预测 à 将预测和标签传递给损失函数得到损失 à 反向调用损失函数，计算梯度 à step继续更新权值 【这就是一个周期，之后就是迭代重复这个过程】

 

（网络的参数是网络的权重，优化后可以在网络中更新权重；梯度存储在网络参数中的权重张量中）

P26 构建CNN的训练循环

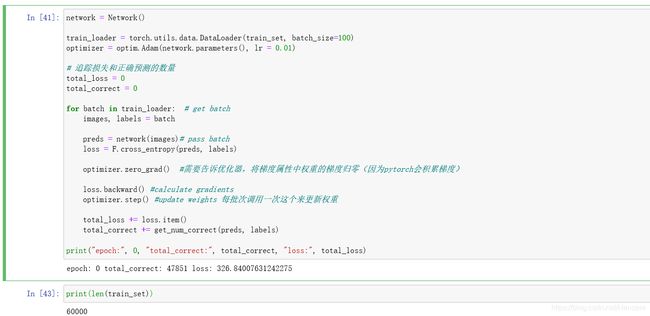
为了训练神经网络，建立了训练循环，构建一个循环，遍历所有批次的训练循环

即处理所有的批次而不是一个

正确率：

迭代的次数：60000个数据/100 = 600，得到600，所以要做600个批次或者说600个迭代；

每次改变batch_size（之前batch=100），也就改变了更新权值的次数，也就是向损失函数最小的方向前进的步数。每一批次通过调用optimizer.step()来更新权值，也就是我们要向损失函数最小值迈进600步

 

大循环

这是一次循环（也就是对一组数据集，进行了600次循环），接下来是就是要对这组600次循环进行5次

加了一个for epoch in range（5）：

可以看到在第5个周期，上升速度放缓，这时就要考虑调整或改变超参数

此时正确率：

P27 混淆矩阵

构建并解释一个混淆矩阵（confusion matrix）来分析神经网络的训练结果

构建一些函数，可以得到训练集中的每个样本的预测张量

混淆矩阵可以看到我们的网络将哪些类之间彼此混淆了

 

我们创建这个混淆矩阵，需要有一个预测的张量和一个有相应的真值或标签的张量（也就是说一个矩阵，在x轴是预测值，y轴是真实值，都是t-shirt、bag……10个标签）

 

我们希望是对角线，因为对角线是预测的标签等于真实标签的地方，每个格里的值是指当预测值==真实值的时候（比如t-shirt），网络预测为t-shirt的次数

 

除了对角线以外的比较大的值，就是混淆矩阵的值

Now：取所有的类别，需要在x轴和y轴运行他们，然后对所有的预测和相应的真实标签进行迭代，只要计算出每个方块中有多少次发生，就会给我们一个混乱矩阵

 

准备阶段

建立一个函数，函数将通过整个训练集并且产生一个预测get_all_preds，传递给函数模型（网络），和数据加载器（生成批量），因为我们将训练集分成几个部分，然后每次都进行预测。

先把所有的预测收集成一个张量，遍历数据加载器中的所有批次，我们将通过加载器中创建批处理循环来迭代这个数据加载器，然后解压缩，然后将图像传递给一个模型并返回对该批次的预测，最后将这些预测连接到所有的预测张量（使用torch.cat函数）

 

创建一个预测加载器（是一个数据加载器），将传输我们的训练集，将网络和数据加载器传递给这个函数，获取刚刚定义的所有线程

可以看到是一个60000*10的矩阵，就是有60000个样本，10个预测标签，具有最高预测价值的类别是网络预测最强烈的所以要看哪个是最高的，使用Argmax函数

 

因为我们需要在不跟踪梯度的情况下得到我们的预测，所以不需要创建图表

之前是全局关闭跟踪，现在有局部关闭的，使用关键字torch.no_grad

再检查：就是false了

建立矩阵

需要标签，需要一个相应的预测张量，用argmax知道最大值

将预测与目标配对，调用torch.stack函数

stack用法：见这个博客

https://blog.csdn.net/Teeyohuang/article/details/80362756

 

于是现在就可以遍历stack之后的所有对，并计算每次组合发生的次数tolist，变成列表

然后创建一盒混淆矩阵，调用torch.zeros，10,10是因为训练集有10个类别