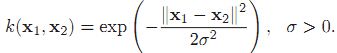胡萝卜(3)
目录
- 目录
- 1、struct和class区别,你更倾向用哪个
- 2、kNN,朴素贝叶斯,SVM的优缺点,各种算法优缺点
- 3、10亿个整数,1G内存,O(n)算法,统计只出现一次的数。
- 4、海量数据排序
- 5、项目中的数据是否会归一化处理,哪个机器学习算法不需要归一化处理
- 6、RBF核与高斯核的区别
- 7、L1和L2的区别
- 8、有哪些聚类方法?
- 9、什么是模糊聚类,还有划分聚类,层次聚类等
- 10、哪些模型容易过拟合,模型怎么选择
- 11、CART、GBDT
- 12、写SVM的优化形式,用拉格朗日公式推导SVM kernel变换
- 13、数据结构当中的树,都有哪些
- 14、二分查找算法,递归、非递归实现,分析时间复杂度
- 15、几个排序算法,必须写出(快排)
- 快速排序
1、struct和class区别,你更倾向用哪个
结构与类共享几乎所有相同的语法,但结构比类受到的限制更多:
1、尽管结构的静态字段可以初始化,结构实例字段声明还是不能使用初始值设定项。
2、结构不能声明默认构造函数(没有参数的构造函数)或析构函数。
3、结构的副本由编译器自动创建和销毁,因此不需要使用默认构造函数和析构函数。实际上,编译器通过为所有字段赋予默认值(参见默认值表)来实现默认构造函数。结构不能从类或其他结构继承。
4、结构是值类型——如果从结构创建一个对象并将该对象赋给某个变量,变量则包含结构的全部值。
结构具有以下特点:
- 结构是值类型,而类是引用类型。
- 向方法传递结构时,结构是通过传值方式传递的,而不是作为引用传递的。
- 与类不同,结构的实例化可以不使用 new 运算符。
- 结构可以声明构造函数,但它们必须带参数。
- 一个结构不能从另一个结构或类继承,而且不能作为一个类的基。
- 所有结构都直接继承自 System.ValueType,后者继承自 System.Object。
- 结构可以实现接口。
- 在结构中初始化实例字段是错误的
2、kNN,朴素贝叶斯,SVM的优缺点,各种算法优缺点
参考:
http://bbs.pinggu.org/thread-2604496-1-1.html
https://www.cnblogs.com/94julia/p/3294464.html
https://zhuanlan.zhihu.com/p/27160995
(朴素贝叶斯的核心思想,有没有考虑属性之间不是相互独立的情况)
- 朴素贝叶斯核心思想利用先验概率得到后验概率,并且最终由期望风险最小化得出后验概率最大化,从而输出让后验概率最大化的值(具体概率与先验概率由加入拉普拉斯平滑的极大似然估计而成的贝叶斯估计得到),特征必须相互独立。
(1)KNN的优缺点
KNN算法的优点:
- 简单、有效。
- 重新训练的代价较低
- 计算时间和空间 线性于 训练集的规模
- 由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
- 该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
KNN算法缺点:
- KNN算法是懒散学习方法(lazy learning,基本上不学习),一些积极学习的算法要快很多。
- 类别评分不是规格化的(不像概率评分)。
- 输出的可解释性不强,例如决策树的可解释性较强。
- 该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
- 计算量较大。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
(2)朴素贝叶斯的优缺点
优点:
- 朴素贝叶斯模型发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。
- NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。
缺点:
- 理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的(可以考虑用聚类算法先将相关性较大的属性聚类),这给NBC模型的正确分类带来了一定影响。在属性个数比较多或者属性之间相关性较大时,NBC模型的分类效率比不上决策树模型。而在属性相关性较小时,NBC模型的性能最为良好。
- 需要知道先验概率。
- 分类决策存在错误率
(3)SVM的优缺点
SVM的优点:
- 可以解决小样本情况下的机器学习问题。
- 可以提高泛化性能。
- 可以解决高维问题。
- 可以解决非线性问题。
- 可以避免神经网络结构选择和局部极小点问题。
SVM的缺点:
- 对缺失数据敏感。
- 对非线性问题没有通用解决方案,必须谨慎选择Kernel function来处理。
(4)人工神经网络的优缺点
人工神经网络的优点:
- 分类的准确度高
- 并行分布处理能力强,分布存储及学习能力强
- 对噪声神经有较强的鲁棒性和容错能力
- 能充分逼近复杂的非线性关系,具备联想记忆的功能等。
人工神经网络的缺点:
- 神经网络需要大量的参数,如网络拓扑结构、权值和阈值的初始值;
- 不能观察之间的学习过程,输出结果难以解释,会影响到结果的可信度和可接受程度;
- 学习时间过长,甚至可能达不到学习的目的
(5)遗传算法的优缺点
遗传算法的优点:
- 与问题领域无关切快速随机的搜索能力。
- 搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较,鲁棒性好。
- 搜索使用评价函数启发,过程简单。
- 使用概率机制进行迭代,具有随机性。
- 具有可扩展性,容易与其他算法结合。
遗传算法的缺点:
- 遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码,
- 另外三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验.没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢,要得要较精确的解需要较多的训练时间。
- 算法对初始种群的选择有一定的依赖性,能够结合一些启发算法进行改进。
(6)决策树(Decision Trees)的优缺点
决策树的优点:
- 决策树易于理解和解释.人们在通过解释后都有能力去理解决策树所表达的意义。
- 对于决策树,数据的准备往往是简单或者是不必要的.其他的技术往往要求先把数据一般化,比如去掉多余的或者空白的属性。
- 能够同时处理数据型和常规型属性。其他的技术往往要求数据属性的单一。
- 决策树是一个白盒模型。如果给定一个观察的模型,那么根据所产生的决策树很容易推出相应的逻辑表达式。
- 易于通过静态测试来对模型进行评测。表示有可能测量该模型的可信度。
- 在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
- 可以对有许多属性的数据集构造决策树。
- 决策树可很好地扩展到大型数据库中,同时它的大小独立于数据库的大小。
决策树的缺点:
- 对于那些各类别样本数量不一致的数据,在决策树当中,信息增益的结果偏向于那些具有更多数值的特征。
- 决策树处理缺失数据时的困难。
- 过度拟合问题的出现。
- 忽略数据集中属性之间的相关性。
(7)Adaboosting方法的优点
- adaboost是一种有很高精度的分类器。
- 可以使用各种方法构建子分类器,Adaboost算法提供的是框架。
- 当使用简单分类器时,计算出的结果是可以理解的。而且弱分类器构造极其简单。
- 简单,不用做特征筛选。
- 不用担心overfitting。
3、10亿个整数,1G内存,O(n)算法,统计只出现一次的数。
方案一:分拆然后分布式
方案二:对应每个数有三个状态,01代表出现一次,统计10亿以内数据,然后看最终哪些是01状态
4、海量数据排序
位操作
5、项目中的数据是否会归一化处理,哪个机器学习算法不需要归一化处理
量纲问题:归一化有利于优化迭代速度(梯度下降),提高精度(KNN)
SVM需要归一化
LDA、DT 不需要归一化
6、RBF核与高斯核的区别
高斯是RBF函数的一种特例
7、L1和L2的区别
参考:https://www.zhihu.com/question/26485586
L1是蓝色的线,L2是红色的线,很明显,L1的分布对极端值更能容忍。
那么如果数据损失项使用L1 Norm,很明显,L1 Norm对outlier没有L2 Norm那么敏感;如果正则化损失项使用L1的话,那么使学习到的参数倾向于稀疏,使用L2 Norm则没有这种倾向。
- L1优点是能够获得sparse模型,对于large-scale的问题来说这一点很重要,因为可以减少存储空间。缺点是加入L1后目标函数在原点不可导,需要做特殊处理。
- L2优点是实现简单,能够起到正则化的作用。缺点就是L1的优点:无法获得sparse模型。实际上L1也是一种妥协的做法,要获得真正sparse的模型,要用L0正则化。
L0:计算非零个数,用于产生稀疏性,但是在实际研究中很少用,因为L0范数很难优化求解,是一个NP-hard问题,因此更多情况下我们是使用L1范数
L1:计算绝对值之和,用以产生稀疏性,因为它是L0范式的一个最优凸近似,容易优化求解
L2:计算平方和再开根号,L2范数更多是防止过拟合,并且让优化求解变得稳定很快速(这是因为加入了L2范式之后,满足了强凸)。
8、有哪些聚类方法?
参考:http://blog.csdn.net/alex_luodazhi/article/details/47125149
常用聚类算法:
- K-means聚类
- 层次聚类
- SOM聚类(SOM神经网络)
- FCM聚类
- 谱聚类
- 模糊聚类
(1)K-means聚类
优点:
简单直接,易于理解,在低维数据集上有不错的效果。
缺点:
对于高维数据,其计算速度十分慢,主要是慢在计算距离上,它的另外一个缺点就是它需要我们设定希望得到的聚类数k,若我们对于数据没有很好的理解,那么设置k值就成了一种估计性的工作。
(2)层次聚类
优点:
1,距离和规则的相似度容易定义,限制少;
2,不需要预先制定聚类数;
3,可以发现类的层次关系(在一些特定领域如生物有很大作用);
缺点:
1,计算复杂度太高(考虑并行化);
2,奇异值也能产生很大影响;
3,算法很可能聚类成链状(一层包含着一层);
9、什么是模糊聚类,还有划分聚类,层次聚类等
模糊聚类分析一般是指根据研究对象本身的属性来构造模糊矩阵,并在此基础上根据一定的隶属度来确定聚类关系,即用模糊数学的方法把样本之间的模糊关系定量的确定,从而客观且准确地进行聚类。
聚类就是将数据集分成多个类或簇,使得各个类之间的数据差别应尽可能大,类内之间的数据差别应尽可能小,即为“最小化类间相似性,最大化类内相似性”原则 。
10、哪些模型容易过拟合,模型怎么选择
(1)出现过拟合
决策树 DT
神经网络
SVM也会出现过拟合(核函数的系数选择,太大容易过拟合)
KNN近邻,K太小
(2)模型选择
参考:http://blog.csdn.net/bbbeoy/article/details/72571855?locationNum=7&fps=1
从训练集划分点数据出来形成验证集来近似测试误差;
对训练误差进行某种转化来近似测试误差。
![]()
11、CART、GBDT
KNN(分类与回归)
CART
- 回归树用平方误差最小化准则
- 分类树用基尼指数最小化准则
Logistics(推导)
GBDT
- 利用损失函数的负梯度在当前模型的值作为回归问题提升树算法中的残差的近似值,拟合一个回归树
随机森林
- Bagging+CART
12、写SVM的优化形式,用拉格朗日公式推导SVM kernel变换
- SVM 凸优化问题
- 拉格朗日对偶(min和max交换顺序得到对偶问题)
引入拉格朗日因子
![]()
最小化问题中,包含着最大化问题,对偶后得到
![]()
求导=0,带入后得到(被称为KKT条件)
![]()
SVM最佳化形式转化为只与αn有关
![]()
其中,满足最佳化的条件称之为Karush-Kuhn-Tucker(KKT)
13、数据结构当中的树,都有哪些
参考博客:http://blog.csdn.net/hero_myself/article/details/52080969
二叉树、满二叉树、完全二叉树、二叉排序树、平衡二叉树
B树、B+树、红黑树、键树、字典树、区间树与线段树、败者树与胜者树
14、二分查找算法,递归、非递归实现,分析时间复杂度
#include
using namespace std;
/*
二分查找思想:
1、数组从小到大排序;
2、查找的key每次和中间数比较,如果key小于mid 查找mid左侧的数组部分;
如果key大于mid,则查找mid右侧的数组部分;如果相等,则直接返回mid。
输入:排序数组-array,数组大小-aSize,查找值-key
返回:返回数组中的相应位置,否则返回-1
*/
//非递归查找
int BinarySearch(int *array, int aSize, int key)
{
if (array == NULL || aSize == 0 )
return -1;
int low = 0;
int high = aSize - 1;
int mid = 0;
while ( low <= high )
{
mid = (low + high )/2;
if ( array[mid] < key)
low = mid + 1;
else if ( array[mid] > key )
high = mid - 1;
else
return mid;
}
return -1;
}
//递归
int BinarySearchRecursive(int *array, int low, int high, int key)
{
if ( low > high )
return -1;
int mid = ( low + high )/2;
if ( array[mid] == key )
return mid;
else if ( array[mid] < key )
return BinarySearchRecursive(array, mid+1, high, key);
else
return BinarySearchRecursive(array, low, mid-1, key);
}
int main()
{
int array[10];
for (int i=0; i<10; i++)
array[i] = i;
cout<<"No recursive:"<cout<<"position:"<array, 10, 6)<cout<<"recursive:"<cout<<"position:"<array, 0, 9, 6)<return 0;
}
二分查找的基本思想是将n个元素分成大致相等的两部分,去a[n/2]与x做比较,
- 如果x = a[n/2],则找到x,算法中止;
- 如果x < a[n/2],则只要在数组a的左半部分继续搜索x
- 如果x > a[n/2],则只要在数组a的右半部搜索x
时间复杂度无非就是while循环的次数!
总共有n个元素,渐渐跟下去就是n,n/2,n/4,….n/2^k,其中k就是循环的次数
由于你n/2^k取整后>=1,即令n/2^k=1
可得k=log2n,(是以2为底,n的对数)
所以时间复杂度可以表示O()=O(log2n)
15、几个排序算法,必须写出(快排)
参考:https://www.cnblogs.com/huangliang-hb/p/5760679.html
http://blog.csdn.net/jd_19900903/article/details/39965523
- 插入排序:时间复杂度,最坏 O(n2) O ( n 2 ) ,最好不需要移动
- 冒泡排序:最坏时间复杂度为 O(n2) O ( n 2 ) 。 算法的平均时间复杂度为 O(n2) O ( n 2 ) 。冒泡排序最好的时间复杂度为O(n)
- 快速排序:最理想 O(nlogn) 最差时间 O(n2) O ( n 2 ) 平均复杂度O(nlogn)
- 堆排序:时间复杂度 最理想 O(nlogn) 最差时间O(nlogn) 平均复杂度O(nlogn)
快速排序
参考:http://blog.csdn.net/zhengjuexi4456/article/details/52594890
- 最理想 O(nlogn) O ( n l o g n )
- 最差时间 O(n2) O ( n 2 )
- 平均复杂度 O(nlogn) O ( n l o g n )
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
算法步骤:
1 从数列中挑出一个元素,称为 “基准”(pivot)
2 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
3 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。 递归的最底部情形,是数列的大小是0或1,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
快速排序是基于分治模式处理的,对一个典型子数组A[p…r]排序的分治过程为三个步骤:
1.分解:
A[p..r]被划分为俩个(可能空)的子数组A[p ..q-1]和A[q+1 ..r],
使得 A[p ..q-1] <= A[q] <= A[q+1 ..r]
2.解决:
通过递归调用快速排序,对子数组A[p ..q-1]和A[q+1 ..r]排序。
3.合并。
Partition过程:假设数组{6,10,10,3,7,1,8}
(1)从前都和8比较,6小于8,自己和自己交换,不变
(2)10大于8,不进入if
(3)10大于8,不进入if
(4)3小于8,交换到10之前
(5)7小于8,交换到10之前
(6)1小于8,交换到10之前
![]()
#include 排序前:
12 4 34 6 8 65 3 2 988 45
排序后:
2 3 4 6 8 12 34 45 65 988