PyTorch框架学习十九——模型加载与保存
PyTorch框架学习十九——模型加载与保存
- 一、序列化与反序列化
- 二、PyTorch中的序列化与反序列化
-
- 1.torch.save
- 2.torch.load
- 三、模型的保存
-
- 1.方法一:保存整个Module
- 2.方法二:仅保存模型参数
- 四、模型的加载
-
- 1.加载整个模型
- 2.仅加载模型参数
- 五、断点续训练
-
- 1.断点续训练的模型保存
- 2.断点续训练的模型加载
距离上次的学习笔记时隔了正好一个月。。。下面继续!
其实深度学习的五大步骤——数据、模型、损失函数、优化器和迭代训练,这些用PyTorch的基本实现前面的笔记都已经涉及,最后的几次笔记是一些实用的技巧,PyTorch框架的基础学习就将告一段落,后面开始Paper的学习,有精力的话也一定会更新。
一、序列化与反序列化
这里先介绍一下内存与硬盘的区别,这两种存储设备最重要的区别是内存的内容不会永久保存,在程序运行结束或是断电等情况下,数据会全部丢失,而在硬盘里的数据则不受上述的影响。所以我们有必要将一些值得长久保存的东西,比如训练好的模型、关键的数据等从内存中转存到硬盘中,下次使用的时候再从硬盘中读取到内存。
- 序列化:将数据从内存转存到硬盘。
- 反序列化:将数据从硬盘转存到内存。
具体见下图所示:

序列化与反序列化的主要目的是:可以使得数据/模型可以长久地保存。
二、PyTorch中的序列化与反序列化
1.torch.save
torch.save(obj, f, pickle_module=<module 'pickle' from '/opt/conda/lib/python3.6/pickle.py'>, pickle_protocol=2, _use_new_zipfile_serialization=True)
- obj:需要保存的对象。
- f:保存的路径。
2.torch.load
torch.load(f, map_location=None, pickle_module=<module 'pickle' from '/opt/conda/lib/python3.6/pickle.py'>, **pickle_load_args)
- f:加载文件的路径。
- map_location:指定存放的位置,cpu或gpu。
三、模型的保存
1.方法一:保存整个Module
torch.save(net, path)
下面构建一个简单的网络模型作为例子:
import torch
import numpy as np
import torch.nn as nn
# 构建一个LeNet网络模型,并实例化为net
class LeNet2(nn.Module):
def __init__(self, classes):
super(LeNet2, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 6, 5),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(6, 16, 5),
nn.ReLU(),
nn.MaxPool2d(2, 2)
)
self.classifier = nn.Sequential(
nn.Linear(16*5*5, 120),
nn.ReLU(),
nn.Linear(120, 84),
nn.ReLU(),
nn.Linear(84, classes)
)
def forward(self, x):
x = self.features(x)
x = x.view(x.size()[0], -1)
x = self.classifier(x)
return x
def initialize(self):
for p in self.parameters():
p.data.fill_(20191104)
net = LeNet2(classes=2019)
忽略训练过程,真实的训练不应该这样。。。,这里为了简单,只是人为地改变了一下参数权重,并不是训练得到的结果。
# "训练"
print("训练前: ", net.features[0].weight[0, ...])
net.initialize()
print("训练后: ", net.features[0].weight[0, ...])
(虚假)结果:
训练前: tensor([[[-0.0065, -0.0388, 0.0194, -0.0944, -0.0539],
[-0.0981, 0.0611, -0.0066, -0.0140, 0.0849],
[ 0.0495, -0.0793, -0.0424, 0.0282, 0.0338],
[ 0.0523, -0.0409, -0.1071, -0.0623, 0.0956],
[-0.0385, 0.0554, 0.0160, 0.0671, 0.0913]],
[[ 0.0409, 0.0811, -0.0677, 0.1040, -0.0236],
[-0.0717, -0.0418, 0.0007, 0.0950, -0.0309],
[-0.0089, 0.0140, -0.0855, 0.0818, -0.0270],
[ 0.0316, -0.0637, 0.0093, 0.0669, -0.1031],
[-0.0337, 0.1068, -0.0927, -0.1069, 0.0267]],
[[-0.0034, 0.0862, 0.0743, -0.0082, 0.0929],
[-0.0738, 0.0781, -0.0701, -0.0327, -0.0553],
[-0.0951, -0.0604, -0.0906, 0.0169, 0.0084],
[ 0.0589, 0.0391, 0.0493, 0.1018, 0.0563],
[ 0.0407, -0.0053, 0.0307, 0.0077, 0.0262]]],
grad_fn=<SelectBackward>)
训练后: tensor([[[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.]],
[[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.]],
[[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.]]],
grad_fn=<SelectBackward>)
好,通过上面的偷懒操作,视为我们训练好了模型,现在需要保存这个模型,方法一是保存整个模型,如下图所示:
path_model = "./model.pkl"
torch.save(net, path_model)
此时查看当前目录,多了一个model.pkl的文件,这个就是保存的模型文件:
![]()
这是一个简单的模型,如果模型比较庞大的话,这种方法会有一个问题,就是保存耗时较长,占用内存也较大,所以一般不这样保存。
2.方法二:仅保存模型参数
我们回顾一下模型的内容,一个模型它是有很多部分组成的,就像刚刚构建的LeNet,其模型所包含的内容就如下所示:

而我们可以观察一下,在模型的训练过程中,只有参数_parameters是不断被更新的,那么我们可以在保存的时候仅保存模型参数,其他的部分在用的时候可以重新构建,然后将参数加载到新构建的模型上就等同于是保存了整个模型,这样不仅可以节省保存的时间也能减小内存加载的消耗。
这种方法的保存代码为:
net_state_dict = net.state_dict()
torch.save(net_state_dict, path)
这里使用了state_dict()函数,返回了一个字典,包含了这个模型的所有参数。
还是以刚刚的LeNet为例,只需将保存的代码改为:
path_state_dict = "./model_state_dict.pkl"
# 保存模型参数
net_state_dict = net.state_dict()
torch.save(net_state_dict, path_state_dict)
即可。
可以通过单步调试查看net_state_dict 的内容:
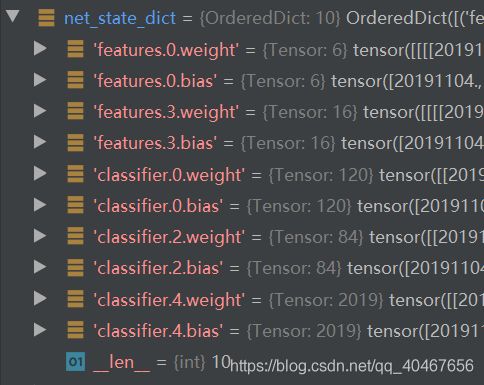
它的确包含了每一层的权重和偏置,而在当前目录下多了一个名为model_state_dict.pkl的保存文件。
![]()
四、模型的加载
这个都是和三中的两种方法对应,保存的时候是整个模型就加载整个模型,保存的时候是仅保存模型参数就先构建模型然后加载模型参数。
1.加载整个模型
import torch
import numpy as np
import torch.nn as nn
class LeNet2(nn.Module):
def __init__(self, classes):
super(LeNet2, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 6, 5),
nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(6, 16, 5),
nn.ReLU(),
nn.MaxPool2d(2, 2)
)
self.classifier = nn.Sequential(
nn.Linear(16*5*5, 120),
nn.ReLU(),
nn.Linear(120, 84),
nn.ReLU(),
nn.Linear(84, classes)
)
def forward(self, x):
x = self.features(x)
x = x.view(x.size()[0], -1)
x = self.classifier(x)
return x
def initialize(self):
for p in self.parameters():
p.data.fill_(20191104)
# ================================== load net ===========================
flag = 1
# flag = 0
if flag:
path_model = "./model.pkl"
net_load = torch.load(path_model)
print(net_load)
输出:
LeNet2(
(features): Sequential(
(0): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(4): ReLU()
(5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(classifier): Sequential(
(0): Linear(in_features=400, out_features=120, bias=True)
(1): ReLU()
(2): Linear(in_features=120, out_features=84, bias=True)
(3): ReLU()
(4): Linear(in_features=84, out_features=2019, bias=True)
)
)
注意:在加载之前一定要先定义模型LeNet,定义必须和保存时的一致,不然会对应不上。
2.仅加载模型参数
这种方法需要比前一种方法多一步:实例化模型。即先得有一个模型才能对它加载参数。
# ================================== load state_dict ===========================
flag = 1
# flag = 0
if flag:
# 加载参数到内存,并查看keys
path_state_dict = "./model_state_dict.pkl"
state_dict_load = torch.load(path_state_dict)
print(state_dict_load.keys())
# 实例化模型
net_new = LeNet2(classes=2019)
# 更新参数到模型,等同于加载整个模型
print("加载前: ", net_new.features[0].weight[0, ...])
net_new.load_state_dict(state_dict_load)
print("加载后: ", net_new.features[0].weight[0, ...])
输出:
odict_keys(['features.0.weight', 'features.0.bias', 'features.3.weight', 'features.3.bias', 'classifier.0.weight', 'classifier.0.bias', 'classifier.2.weight', 'classifier.2.bias', 'classifier.4.weight', 'classifier.4.bias'])
加载前: tensor([[[ 0.1004, -0.0658, -0.0483, -0.0398, 0.0197],
[ 0.0157, 0.0474, -0.0996, -0.0778, -0.0177],
[-0.0889, -0.0732, -0.0625, 0.1042, 0.1082],
[ 0.0360, -0.0571, 0.0523, -0.0154, -0.0241],
[ 0.0427, 0.0968, 0.0166, 0.0405, -0.0782]],
[[ 0.0610, 0.0467, 0.0285, 0.0061, 0.0146],
[-0.0410, 0.0822, -0.0535, 0.0842, -0.0443],
[ 0.1010, 0.0972, -0.0625, -0.1114, 0.0899],
[ 0.0462, -0.0121, 0.0476, 0.0673, 0.0900],
[ 0.1030, -0.0278, 0.0374, -0.0098, -0.0929]],
[[ 0.0703, 0.0600, -0.0538, 0.0179, -0.0008],
[ 0.1119, 0.0187, 0.0359, -0.0721, 0.0033],
[-0.0225, 0.0788, -0.1081, 0.0700, 0.0269],
[ 0.0519, -0.0959, -0.0329, -0.0520, -0.0741],
[ 0.1020, 0.0321, 0.0549, -0.0522, -0.0783]]],
grad_fn=<SelectBackward>)
加载后: tensor([[[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.]],
[[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.]],
[[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.],
[20191104., 20191104., 20191104., 20191104., 20191104.]]],
grad_fn=<SelectBackward>)
五、断点续训练
这是一个非常实用的技巧,设想你的一个模型训练了五天,然后因为断电等不可控原因突然中止,是不是非常抓狂。
断点续训练的思想就是,在训练的过程中,每隔一定数量的epoch就保存一次模型(参数),若程序中断,可以从离中断最近位置保存的文件中加载模型(参数)继续训练。
1.断点续训练的模型保存
在训练过程中,只有模型与优化器中会有与训练相关的数据,比如模型的参数权重、优化器中的学习率等等,以及还需要记录一下保存时的epoch,所以我们可以构建这样一个字典,存放刚刚所说的三类数据:
checkpoint = {"model_state_dict": net.state_dict(),
"optimizer_state_dict": optimizer.state_dict(),
"epoch": epoch}
将这个checkpoint保存为pkl文件即可。
if (epoch+1) % checkpoint_interval == 0:
checkpoint = {"model_state_dict": net.state_dict(),
"optimizer_state_dict": optimizer.state_dict(),
"epoch": epoch}
path_checkpoint = "./checkpoint_{}_epoch.pkl".format(epoch)
torch.save(checkpoint, path_checkpoint)
其中checkpoint_interval 就是每隔多少个epoch保存一次上述信息。
下面我们人为构建一个中断,模型、损失函数、优化器、迭代训练部分的代码省略:
if epoch > 5:
print("训练意外中断...")
break
结果如下所示:
Training:Epoch[000/010] Iteration[010/012] Loss: 0.6753 Acc:53.75%
Valid: Epoch[000/010] Iteration[003/003] Loss: 0.4504 Acc:57.37%
Training:Epoch[001/010] Iteration[010/012] Loss: 0.3928 Acc:83.75%
Valid: Epoch[001/010] Iteration[003/003] Loss: 0.0130 Acc:85.79%
Training:Epoch[002/010] Iteration[010/012] Loss: 0.1717 Acc:93.12%
Valid: Epoch[002/010] Iteration[003/003] Loss: 0.0027 Acc:92.11%
Training:Epoch[003/010] Iteration[010/012] Loss: 0.1100 Acc:95.62%
Valid: Epoch[003/010] Iteration[003/003] Loss: 0.0003 Acc:96.32%
Training:Epoch[004/010] Iteration[010/012] Loss: 0.0321 Acc:98.12%
Valid: Epoch[004/010] Iteration[003/003] Loss: 0.0000 Acc:98.42%
Training:Epoch[005/010] Iteration[010/012] Loss: 0.0064 Acc:100.00%
Valid: Epoch[005/010] Iteration[003/003] Loss: 0.0000 Acc:100.00%
Training:Epoch[006/010] Iteration[010/012] Loss: 0.0109 Acc:99.38%
训练意外中断...
当前目录下多了一个pkl文件,其中的4是指保存的第五轮训练后的结果:
![]()
2.断点续训练的模型加载
与正常训练差不多,只是需要在迭代训练之前把上述保存的三种信息加载给模型,使之恢复到断点的状态:
path_checkpoint = "./checkpoint_4_epoch.pkl"
checkpoint = torch.load(path_checkpoint)
# 模型参数更新
net.load_state_dict(checkpoint['model_state_dict'])
# 优化器参数更新
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
# epoch数恢复到断点
start_epoch = checkpoint['epoch']
scheduler.last_epoch = start_epoch
结果如下所示:
Training:Epoch[005/010] Iteration[010/012] Loss: 0.0146 Acc:99.38%
Valid: Epoch[005/010] Iteration[003/003] Loss: 0.0000 Acc:99.47%
Training:Epoch[006/010] Iteration[010/012] Loss: 0.0039 Acc:100.00%
Valid: Epoch[006/010] Iteration[003/003] Loss: 0.0000 Acc:100.00%
Training:Epoch[007/010] Iteration[010/012] Loss: 0.0013 Acc:100.00%
Valid: Epoch[007/010] Iteration[003/003] Loss: 0.0000 Acc:100.00%
Training:Epoch[008/010] Iteration[010/012] Loss: 0.0020 Acc:100.00%
Valid: Epoch[008/010] Iteration[003/003] Loss: 0.0000 Acc:100.00%
Training:Epoch[009/010] Iteration[010/012] Loss: 0.0010 Acc:100.00%
Valid: Epoch[009/010] Iteration[003/003] Loss: 0.0000 Acc:100.00%
可见,epoch继续从5开始,准确率一开始就很高,是紧接着前5次的结果的,再观察损失函数的变化,初始值就很小了:

综上,这样的方法,可以使得因特殊原因中途中断的训练从中断位置继续训练而不用从头开始,非常有用。


