图像二维卷积操作与边缘检测的Python实现(另附canny边缘检测算法)
目录
-
-
- 1、卷积的定义
- 2、卷积在图像处理中的应用
- 图像边缘检测
-
- 利用Sobel和Prewitt算子边缘检测的Python实现
- Canny边缘检测
-
- 1、高斯平滑
- 2、寻找图像中的强度梯度
- 3、非极大抑制Non-maximum suppression
- 4、双阈值检测
- 5、滞后边界跟踪
- 利用OpenCV实现Canny边缘检测
-
1、卷积的定义
卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列x(n)和h(n),则卷积的结果
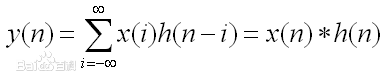
其中星号*表示卷积。当时序n=0时,序列h(-i)是h(i)的时序i取反的结果;时序取反使得h(i)以纵轴为中心翻转180度,所以这种相乘后求和的计算法称为卷积和,简称卷积。另外,n是使h(-i)位移的量,不同的n对应不同的卷积结果。
例:
f(x) =C(k)*g(i),其中C(k)代表卷积操作数,g(i)代表样本数据, f(x)代表输出结果。
假设g(i)是一个一维的函数,而且代表的样本数为G = [1,2,3,4,5,6,7,8,9]
假设C(k)是一个一维的卷积操作数, 操作数为C=[-1,0,1]
则输出结果f(x)可以表示为 F=[1,2,2,2,2,2,2,2,1] (边界数据未处理)
如果卷积的变量是函数x(t)和h(t),则卷积的计算变为

其中p是积分变量,积分也是求和,t是使函数h(-p)位移的量,星号*表示卷积。
(参考百度百科)
2、卷积在图像处理中的应用
绝大多数的图像处理都会用到卷积操作,比如图像去噪,模糊/平滑处理,边缘检测等等。
1、一个简单的数字图像卷积处理流程可以如下:
1)读取源图像像素
2)应用卷积操作数矩阵产生目标图像
3) 对目标图像进行归一化处理
4) 处理边界像素
2、使用模板处理图像相关概念:
模板:矩阵方块,其数学含义是一种卷积运算。
卷积运算:可看作是加权求和的过程,使用到的图像区域中的每个像素分别于卷积核(权矩阵)的每个元素对应相乘,所有乘积之和作为区域中心像素的新值。
卷积核:卷积时使用到的权用一个矩阵表示,该矩阵与使用的图像区域大小相同,其行、列都是奇数,是一个权矩阵。
例:
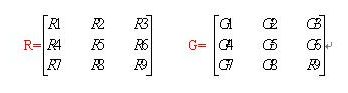
3 * 3 的像素区域R与卷积核G的卷积运算:
R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
图像边缘检测
边缘可以由多种因素引起,如表面的普通分离,深度边缘,表面颜色分离,亮度变化等等。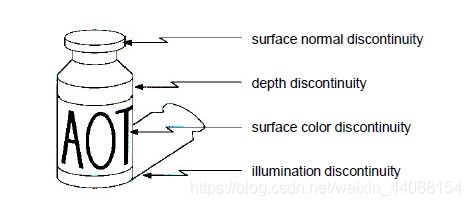
总的来说 ,边缘就是有变化的地方。
在数学中,我们一般用导数来求变化率,推论到图像处理,我们也可以用导数来处理像素的变化。
对于二维函数,它的偏导数为:
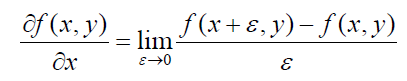
对于离散数据,我们可以使用有限差分进行近似(即令![]()
等于1):

实际计算图像导数时,我们是通过原图像和一个算子进行卷积来完成的(这种方法就是求图像的近似导数)。
常用的边缘检测算子:
1、Sobel算子
Gx=
Gy=
2、Prewitt算子
Gx=

Gy=

利用原图像和x方向Sobel算子/Prewitt算子进行卷积就可以得到图像的x方向导数矩阵Gx,
利用原图像和y方向Sobel算子/Prewitt算子进行卷积就可以得到图像的y方向导数矩阵Gy。
然后利用公式:
![]()
就可以得到图像的梯度矩阵Gxy,这个矩阵包含图像x方向和y方向的边缘信息。
利用Sobel和Prewitt算子边缘检测的Python实现
在scipy库中signal模块的convolve()方法可以用来计算图像卷积。
convolve()的第一个参数是原图像矩阵,第二个参数为卷积算子,指定边界样式为boundary=‘symm’,然后指定关键字参数mode=“same”(输出矩阵大小和原图像矩阵相同)。
import numpy as np
from scipy import signal
from PIL import Image
from matplotlib import pyplot as plt
original = 'C:/Users/DELL4/Desktop/AM.png'#图像路径
img = np.array(Image.open(original).convert("L"))#打开图像并转化为灰度矩阵
#sobel算子
sobel_x = np.array([[-1,0,1],
[-2,0,2],
[-1,0,1]])
sobel_y = np.array([[-1,-2,-1],
[0,0,0],
[1,2,1]])
#prewitt算子
prewitt_x = np.array([[-1, 0, 1],
[ -1, 0, 1],
[ -1, 0, 1]])
prewitt_y = np.array([[-1,-1,-1],
[ 0, 0, 0],
[ 1, 1, 1]])
#计算x方向卷积
img1_x = signal.convolve2d(img,sobel_x,boundary='symm',mode="same")
#计算y方向卷积
img1_y = signal.convolve2d(img,sobel_y,boundary='symm',mode="same")
#得到梯度矩阵
img1_xy = np.sqrt(img1_x**2+img1_y**2)
#梯度矩阵归一到0-255
img1_xy = img1_xy*(255/img1_xy.max())
#prewitt算子计算过程与sobel一样
img2_x = signal.convolve2d(img,prewitt_x,boundary='symm',mode="same")
img2_y = signal.convolve2d(img,prewitt_y,boundary='symm',mode="same")
img2_xy = np.sqrt(img2_x**2+img2_y**2)
img2_xy = img2_xy*(255/img2_xy.max())
#绘制出图像
plt.subplot(1,2,1)
plt.imshow(np.absolute(img1_xy),cmap='gray_r')
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(np.absolute(img2_xy),cmap='gray_r')
plt.axis("off")
plt.show()
结果:(左为sobel检测,右为prewitt检测)

3、Laplace算子
Laplace算子是一个二阶导数的算子,它实际上是一个x方向二阶导数和y方向二阶导数的和的近似求导算子。实际上,Laplace算子是通过Sobel算子推导出来的。
在图像边缘处理中,二阶微分的边缘定位能力更强,锐化效果更好,因此在进行图像边缘处理时,直接采用二阶微分算子而不使用一阶微分。
Laplace算子为

可以看出,该算子在上下左右四个90度的方向上结果相同,也就是说在90度方向上无方向性。为了让其在45度的方向上也具有该性质,对laplace进行扩展定义即Laplace扩展算子
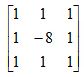
一般在进行Laplace运算之前,我们会先对图像进行先对图像进行模糊平滑处理,目的是去除图像中的高频噪声。
import numpy as np
from scipy import signal
from PIL import Image
from matplotlib import pyplot as plt
original = 'C:/Users/DELL4/Desktop/AM.png'
img = np.array(Image.open(original).convert("L"))
#定义高斯函数
def func(x,y,sigma=1):
return 100*(1/(2*np.pi*sigma))*np.exp(-((x-2)**2+(y-2)**2)/(2.0*sigma**2))
#高斯平滑处理
Gaussian = np.fromfunction(func,(3,3),sigma=3)
img = signal.convolve2d(img,Gaussian,mode="same")
#laplace算子
laplace = np.array([[0,1,0],
[1,-4,1],
[0,1,0]])
#laplace扩展算子
laplace = np.array([[1,1,1],
[1,-8,1],
[1,1,1]])
plt.subplot(1,2,1)
plt.imshow(np.absolute(img_l1),cmap='gray_r')
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(np.absolute(img_l2),cmap='gray_r')
plt.axis("off")
plt.show()
结果:
(左为Laplace算子,右为Laplace扩展算子)

从图中可以看到,其扩展算子检测出的边缘更强一些。
实际上,在Python中已经有了专门用来做检测的库,这里自己写一下主要还为了更深的理解其过程。
Canny边缘检测
Canny边缘检测算法是John F. Canny于 1986 年开发出来的一个多级边缘检测算法。至今仍是边缘检测的一种标准算法,而且仍在研究中广泛使用。
Canny边缘检测一般性步骤:
1)应用高斯滤波来平滑图像,目的是去除噪声
2)计算图像中每个像素点的梯度强度和方向
3)应用非极大值抑制(non-maximum suppression)技术来消除边误检(本来不是但检测出来是)
4)应用双阈值的方法来决定可能的(潜在的)边界
5)通过抑制孤立的弱化边缘最终完成边缘检测(滞后的边界跟踪)
1、高斯平滑
由于边缘检测容易受到图像中噪声的影响,因此第一步是使用5x5高斯滤波器消除图像中的噪声。
高斯滤波器是一种线性滤波器,能够有效地抑制噪声,平滑图像。
高斯滤波器的模板系数随着模板中心的增大而减小。
相对于均值滤波器,对图像的模糊程度较小。
以下为一个3X3高斯滤波器,其中A为原始图像,e为平滑后的图像。

2、寻找图像中的强度梯度
Canny算法的基本思想是找寻一幅图像中灰度强度变化最强的位置。所谓变化最强,即指梯度方向。平滑后的图像中每个像素点的梯度可以由Sobel算子(一种卷积运算)来获得,之后便可利用公式来求得每一个像素点的梯度幅值和角度。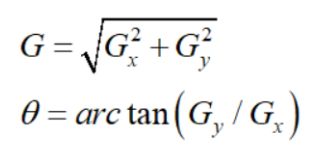
3、非极大抑制Non-maximum suppression
在获得梯度大小和方向后,将对图像进行全面扫描,以去除可能不构成边缘的所有不需要的像素。为此,在每个像素处,检查像素是否是其在梯度方向上附近的局部最大值。
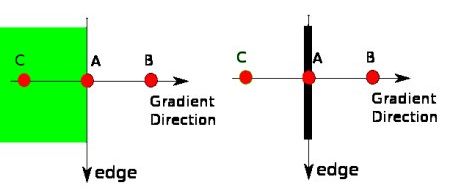
点A在边缘(垂直方向)上。渐变方向垂直于边缘。点B和C在梯度方向上。因此,将A点与B点和C点进行检查,看是否形成局部最大值。如果是这样,则保留,否则将其抑制(置为零)。
4、双阈值检测
设定一个阈值上界和阈值下界(opencv中通常由人为指定的),图像中的像素点如果大于阈值上界则认为必然是边界(称为强边界,strong edge),小于阈值下界则认为必然不是边界,两者之间的则认为是候选项(称为弱边界,weak edge),需进行进一步处理。
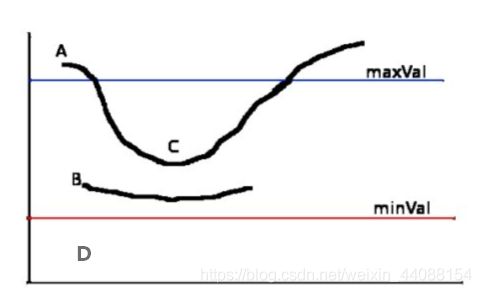
图中,A大于最大阈值,为强边界,保留。B和C位于最大最小之间(成为弱边界),候选,等待进一步判断(第5步)。D小于最小阈值,不是边界,丢弃。
5、滞后边界跟踪
即与强边界相连的位于最大最小阈值之间的弱边界认为是边界,其他的弱边界则被抑制。
如上图,B为弱边界,但他是属于孤立的弱边界,舍弃。C同样也是弱边界,但它与强边界A相连,故其也为边界,保留。
利用OpenCV实现Canny边缘检测
OpenCV中实现Canny边缘检测函数为cv2.Canny().
edge = cv2.Canny(image, threshold1, threshold2[, edges[, apertureSize[, L2gradient ]]])
–image 输入图像.
–threshold1 第一个阈值(低阈值)
–threshold2 第二个阈值(高阈值)
–edges 输出的边缘图像,单通道8位图像。
–aperture_size Sobel 算子内核大小,默认值为3
–L2gradient参数表示一个布尔值,如果为真,则使用更精确的L2范数进行计算(即两个方向的倒数的平方和再开方),否则使用L1范数(直接将两个方向导数的绝对值相加),默认值为真。
import cv2 as cv
from matplotlib import pyplot as plt
import numpy as np
img = 'C:/Users/DELL4/Desktop/AM.png'
img = cv.imread(img,0)#以灰度值读入图像
#高斯平滑
blur = cv.GaussianBlur(img,(5,5),0)#参数可调
#canny函数
edges = cv.Canny(blur,60,180)#参数可调
#绘制图像
plt.subplot(1,2,1),plt.imshow(img,cmap = 'gray')
plt.title('original'),plt.axis("off")
plt.subplot(1,2,2),plt.imshow(edges,cmap = 'gray_r')
plt.title('edges'),plt.axis("off")
plt.show()
参考:
图像处理——卷积原理、二维卷积python实现
python计算机视觉2:图像边缘检测
