DIP笔记4——频率域滤波
1 基础
滤波器：抑制或最小化某些频率的波的装置或材料
频率：自变量变化时，一个周期函数重复相同值序列的次数
PS：滤波器本就是频率域的概念，前面空间域的滤波器 = 邻域 + 对邻域的操作
第一次看到频率域知识，傅里叶函数的复杂直接把我劝退了，还有频谱图，一堆黑白点，也不懂它的含义
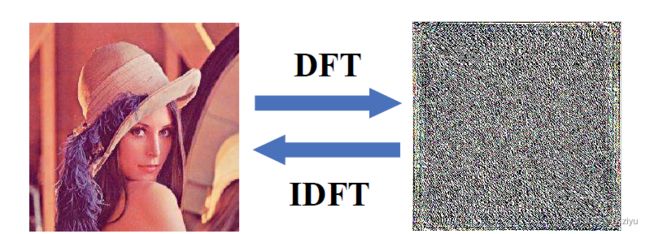
首先，了解一下傅里叶函数以及频率域的知识，这是知乎老哥对傅里叶函数有趣讲解。看完这个后还不够，因为我想知道的是图像上的二维傅里叶变化，以及所谓的频谱图上高频低频分布，每个点的意义
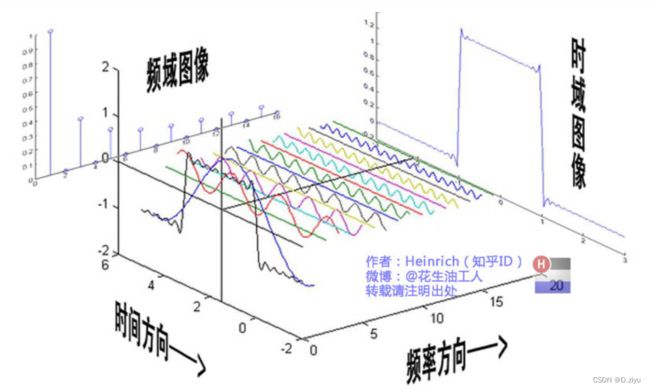
上图可以看到一维的时域图和频域图（这个一维指只有一个自变量改变）。时域图：x为时间，y为幅度；频域图：x为频率，y为幅度。
然后看看二维的图像吧，左图是正常灰度图片，右图可以看作左图的风景照（3d），x,y位置不变，z为高度，也就是左图的灰度值
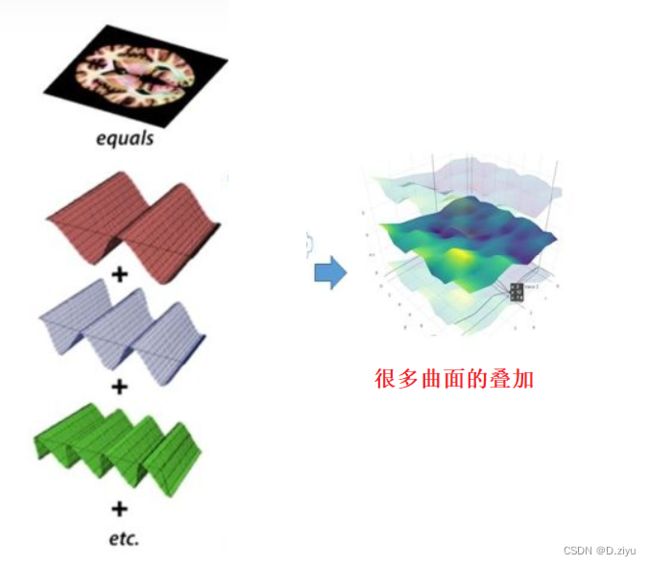
我们知道，一维信号是一维正弦波的总和（知乎那幅图），而二维也是如此，不过这里的正弦波是二维（很多曲面），说明如下图：
好的，到这里已经知道很多东西了，但还是和那副黑乎乎的频谱图没啥关系啊，别急，先来看看什么是频谱。
2 频谱
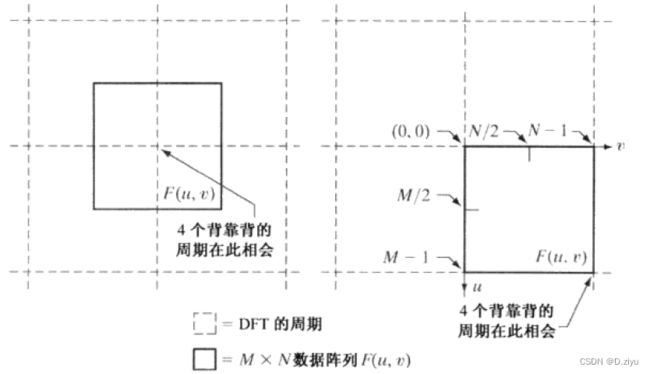
下图中，1.表示图像经过离散傅里叶（DFT）变换 到了频率域，2. 换位中心化
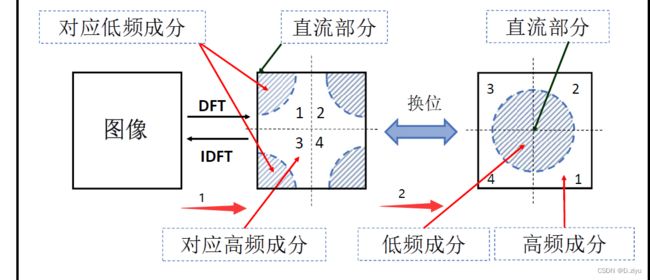
2.1 低频在四周，高频在中心
Q:为什么未中心化时，低频在四周，高频在中心？
想必大家都见过这图，低频高频为什么这样分布？数学推导见知乎，我也没看完这证明
总结就是：二维傅里叶变换是对图像每行做一次一维傅里叶变换,再对其每列做一次一维傅里叶变换,依据从左到右频率增高的原则
Note：一维傅里叶变换得到频率也是由低到高
画几个图，直观感受一下
下图出自DIP第三版，先讲左图（右图是中心化，2.2再说），虚线代表无限周期，实线方框就是DFT得到的频谱（如上图），圆圈部分是F(0,0)，
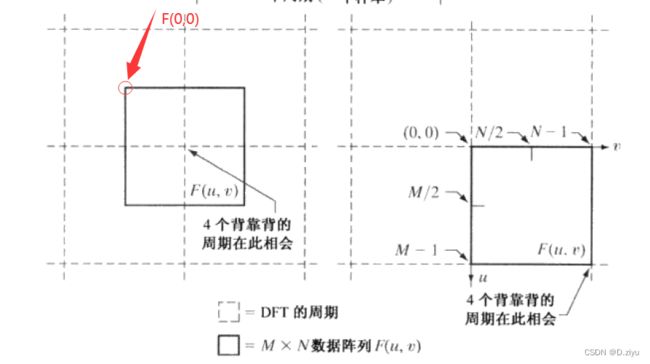
还记得一维频率吗？由低到高。二维频率从中心F（0,0）往外以圆圈的形式由低到高（公式见3）
举例：
2.2 频谱中心化
Q. 为什么要干这事？
人们已经习惯低频位于中央，因为这样把能量集中起来便于使用滤波器，也更方便观察
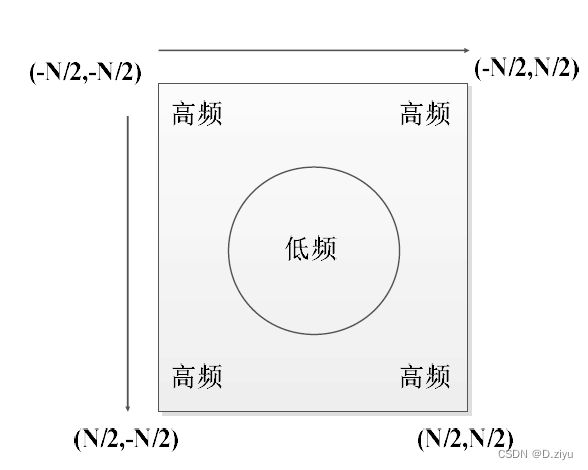
Q:怎么做？
一维情况
先看一维，一个周期是多少？初中就学过，在[-M/2, M/2]，一个周期是M，那很多个周期呢？就是下图了。现在从红线所关注的[0，M]这一个周期看，看到的是 第一个周期函数的右半部分+ 第二个周期函数的左半部分。
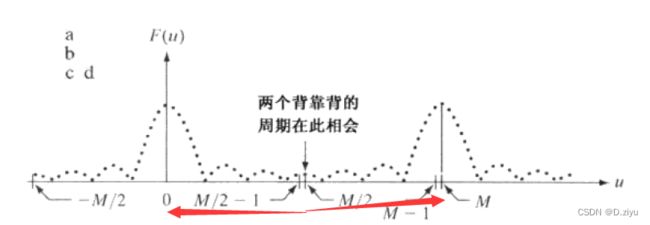
可这样不好看啊，我们想在红线区域（我叫它观察窗口）看的函数长这样：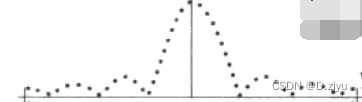
那自然就会做一个平移，平移后：
数学公式：
PS：这里我之前一直不明白怎么就乘(-1)^x，看到欧拉公式终于明白了~
当x等于 π \pi π 时
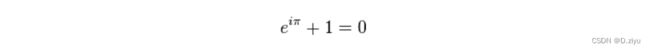
二维情况：
好的，到此你知道一维要平移函数了，那二维呢？同样移动函数
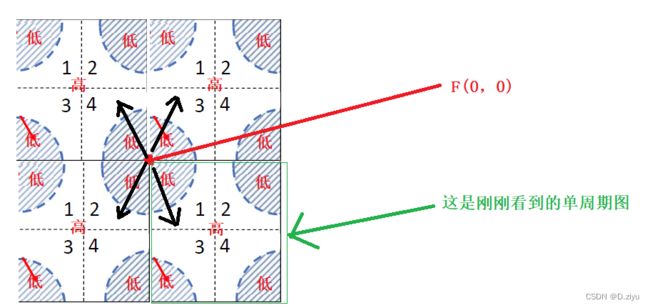
如下图，紫色箭头是平移，其它与上图一致。1–>4, 3–>2, 2–>3, 4–>1，这就是其它地方看到的四个象限交叉改变。
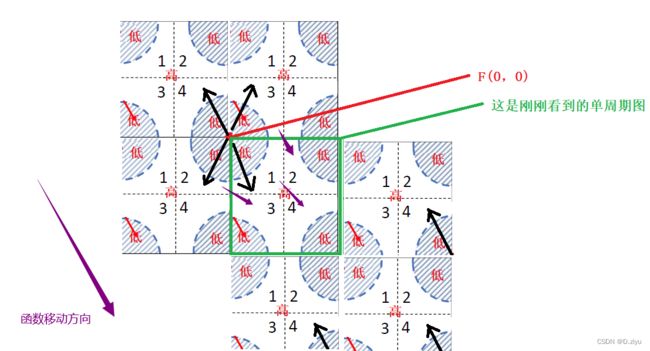
改变后，观察到的单周期内频率图如下：
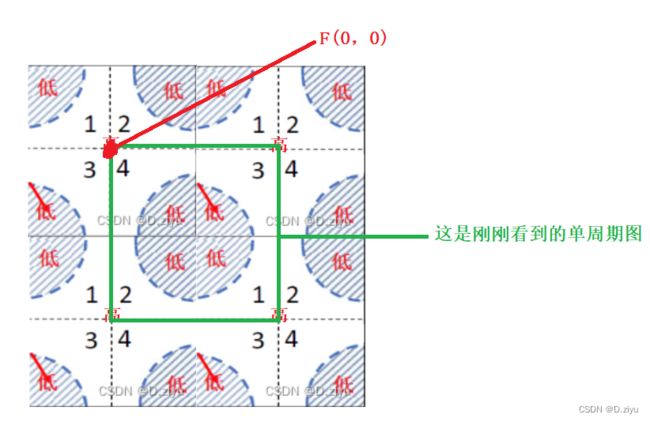
也就是下图中的右图
数学公式：
有了一维的解释，二维也很好懂。中心化到此结束。
Q: 直流分量是啥？
中间那个圈，中间的点就是DC
2.3 频谱意义
那频谱图的意义是啥呢？
图源
频谱中的每一个点：
它到中点的距离描述的是频率
中点到它的方向，是平面波的方向
那一点的灰度值描述的是它的幅度A，这也印证了：频谱图比较亮的地方就是低频，因为图像的能量一般都是集中在低频部分（3-D图见 4能量谱）
由于共轭对称性，频谱中的点关于原点（0，0）是对称的，如图中那两个红点
每个点对应着构成原图的 众多波面的一个
3 相位谱
这个公式其实表明了很多东西，只是我第一次没看懂
相位谱看着没有直观信息，但十分重要。下图说明其重要性
4 能量谱
公式在上面。
我们看到的频谱图像就是这个红框里的，高度就是灰度值，中间峰值高，能量高
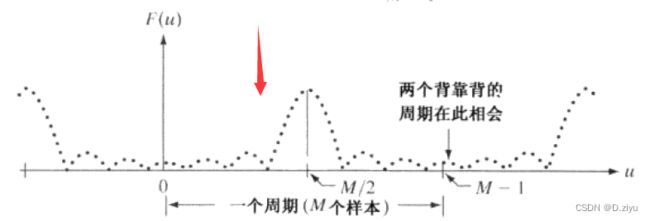
对于一维信号有：F(u)=F*(-u),如图所示的一维信号的幅度谱：点数为M的傅里叶变换一个周期为M，关于原点对称。原点即为0频率点，从图中可以看出在0频率的幅度最大，即信号f(x)的直流分量(均值)，远离原点处的即为高频成份，高频成份的幅值较小，说明信号的大部分能量集中在低频部分。
最后
下图中，上面为原始数据，中间为DFT后的数据，最下面为IDFT后的结果
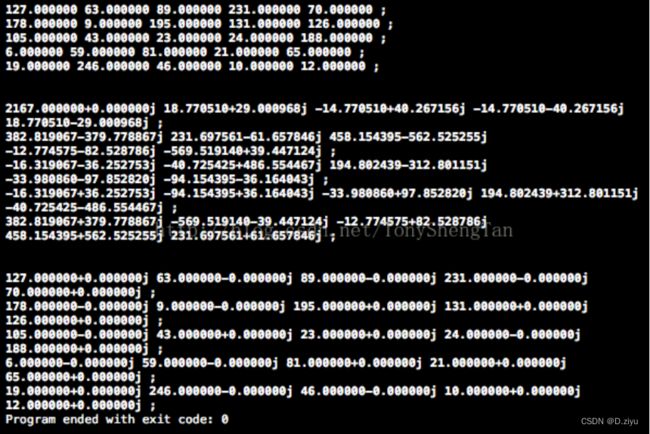
图源
参考1
参考2
参考3