激活函数(sigmoid、tanh、ReLU、softmax)
文章目录
-
- 1.1、sigmoid函数
- 1.2、tanh函数
- 1.3、ReLU函数
- 1.4、softmax函数
激活函数在神经网络中的作用有很多,主要作用是给神经网络提供非线性建模能力。如果没有激活函数,那么再多层的神经网络也只能处理线性可分问题。常用的激活函数有
sigmoid、 tanh、 relu、 softmax等。
1.1、sigmoid函数
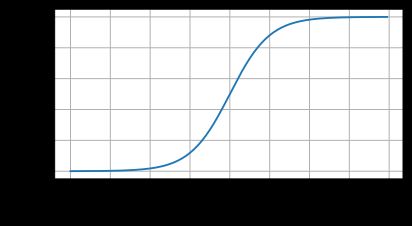
sigmoid函数将输入变换为(0,1)上的输出。它将范围(-inf,inf)中的任意输入压缩到区间(0,1)中的某个值:
s i g m o i d ( x ) = 1 1 + e x p ( − x ) sigmoid(x)=\frac{1}{1+exp(-x)} sigmoid(x)=1+exp(−x)1
sigmoid函数是⼀个⾃然的选择,因为它是⼀个平滑的、可微的阈值单元近似。当我们想要将输出视作⼆元分类问题的概率时, sigmoid仍然被⼴泛⽤作输出单元上的激活函数(你可以将sigmoid视为softmax的特例)。然而, sigmoid在隐藏层中已经较少使⽤,它在⼤部分时候被更简单、更容易训练的ReLU所取代。下面为sigmoid函数的图像表示,当输入接近0时,sigmoid更接近线形变换。
import torch
from d2l import torch as d2l
%matplotlib inline
x=torch.arange(-8.0,8.0,0.1,requires_grad=True)
sigmoid=torch.nn.Sigmoid()
y=sigmoid(x)
d2l.plot(x.detach(),y.detach(),'x','sigmoid(x)',figsize=(5,2.5))
sigmoid函数的导数为下面的公示:
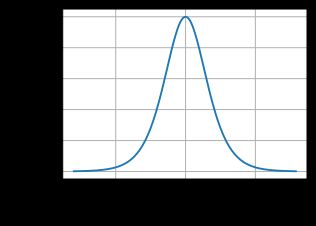
d d x s i g m o i d ( x ) = e x p ( − x ) ( 1 + e x p ( − x ) ) 2 = s i g m o i d ( x ) ( 1 − s i g m o i d ( x ) ) \frac{d}{dx}sigmoid(x)=\frac{exp(-x)}{(1+exp(-x))^2}=sigmoid(x)(1-sigmoid(x)) dxdsigmoid(x)=(1+exp(−x))2exp(−x)=sigmoid(x)(1−sigmoid(x))
sigmoid函数的导数图像如下所示。当输入值为0时,sigmoid函数的导数达到最大值0.25;而输入在任一方向上越远离0点时,导数越接近0。
#清除以前的梯度
#retain_graph如果设置为False,计算图中的中间变量在计算完后就会被释放。
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(),x.grad,'x','grad of sigmoid')
1.2、tanh函数
与sigmoid函数类似,tanh函数也能将其输入压缩转换到区间(-1,1)上,tanh函数的公式如下:
t a n h ( x ) = 1 − e x p ( − 2 x ) 1 + e x p ( − 2 x ) tanh(x)=\frac{1-exp(-2x)}{1+exp(-2x)} tanh(x)=1+exp(−2x)1−exp(−2x)
tanh函数的图像如下所示,当输入在0附近时,tanh函数接近线形变换。函数的形状类似于sigmoid函数,不同的是tanh函数关于坐标系原点中心对称。
import torch
from d2l import torch as d2l
%matplotlib inline
x=torch.arange(-8.0,8.0,0.1,requires_grad=True)
tanh=torch.nn.Tanh()
y=tanh(x)
d2l.plot(x.detach(),y.detach(),'x','tanh(x)',figsize=(5,2.5))
tanh函数的导数是:
d d x t a n h ( x ) = 1 − t a n h 2 ( x ) \frac{d}{dx}tanh(x)=1-tanh^2(x) dxdtanh(x)=1−tanh2(x)
tanh函数的导数如下,当输入接近0时,tanh函数的导数接近最大值1。与sigmoid函数图像中看到的类似,输入在任一方向上远离0点,导数越接近0。
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(),x.grad,'x','grad of tanh',figsize=(5,2.5))
1.3、ReLU函数
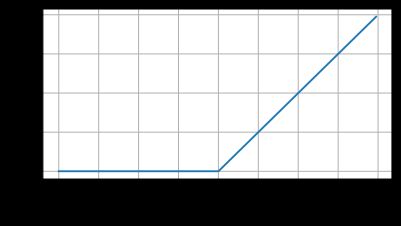
线性整流单元(ReLU),ReLU提供了一种非常简单的非线性变换。给定元素 x x x,ReLU函数被定义为该元素与0的最大值。
R e L U ( x ) = m a x ( x , 0 ) ReLU(x)=max(x,0) ReLU(x)=max(x,0)
ReLU函数通过将相应的活性值设为0,仅保留正元素并丢弃所有负元素。如下为ReLU函数的曲线图。
import torch
from d2l import torch as d2l
%matplotlib inline
x=torch.arange(-8.0,8.0,0.1,requires_grad=True)
relu=torch.nn.ReLU()
y=relu(x)
d2l.plot(x.detach(),y.detach(),'x','relu',figsize=(5,2.5))
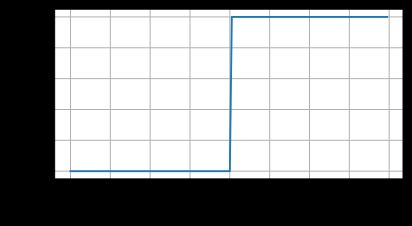
当输入为负时,reLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。当输入值等于0时,ReLU函数不可导。如下为ReLU函数的导数:
f ′ ( x ) = { 1 , x≥0 0 , x<0 f^{'}(x) = \begin{cases} 1, & \text{ x≥0 } \\ 0, & \text{x<0} \end{cases} f′(x)={1,0, x≥0 x<0
#retain_graph如果设置为False,计算图中的中间变量在计算完后就会被释放。
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(),x.grad,'x','grad of relu',figsize=(5,2.5))
ReLU函数的求导表现的很好:要么让参数消失,要么让参数通过。ReLU减轻了神经网络的梯度消失问题。ReLU函数有很多变体,如LeakyReLU,pReLU等。
1.4、softmax函数
在二分类任务时,经常使用sigmoid激活函数。而在处理多分类问题的时候,需要使用softmax函数。它的输出有两条规则。
- 每一项的区间范围的(0,1)
- 所有项相加的和为1.
假设有一个数组V, V i V_i Vi代表V中的第i个元素,那么这个元素的softmax值的计算公式为:
S i = e i ∑ j e j S_i=\frac{e^i}{\sum_j e^j} Si=∑jejei
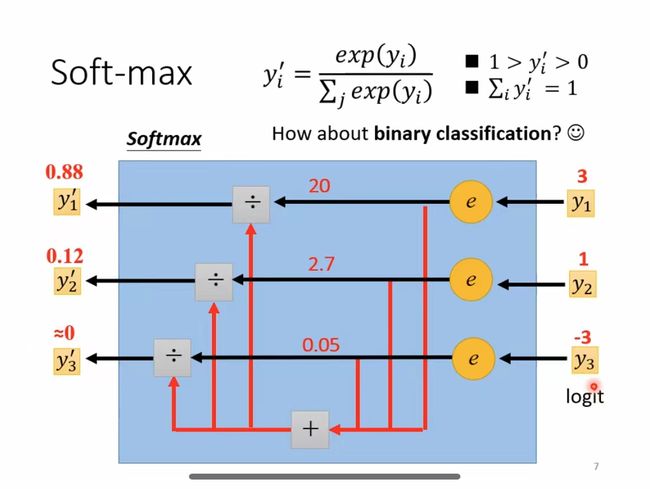
下图为更为详细的计算过程:
如上图所示,输入的数组为[3,1,-3]。那么每项的计算过程为:
当输入为3时,计算公式为 e 3 e 3 + e 1 + e − 3 ≈ 0.88 \frac{e^3}{e^3+e^1+e^{-3}}\approx 0.88 e3+e1+e−3e3≈0.88
当输入为1时,计算公式为 e 1 e 3 + e 1 + e − 3 ≈ 0.12 \frac{e^1}{e^3+e^1+e^{-3}}\approx 0.12 e3+e1+e−3e1≈0.12
当输入为-3时,计算公式为 e − 3 e 3 + e 1 + e − 3 ≈ 0 \frac{e^{-3}}{e^3+e^1+e^{-3}}\approx 0 e3+e1+e−3e−3≈0
下面使用代码实现这一计算过程。
x=torch.Tensor([3.,1.,-3.])
softmax=torch.nn.Softmax(dim=0)
y=softmax(x)
print(y)
tensor([0.8789, 0.1189, 0.0022])
那么在搭建神经网络的时候,应该如何选择激活函数?
- 如果搭建的神经网络的层数不多的时候,选择sigmoid、tanh、relu都可以,如果搭建的网络层数较多的时候,选择不当不当会造成梯度消失的问题,此时一般不宜选择sigmoid、tanh激活函数,最好选择relu激活函数。
- 在二分类问题中,网络的最后一层适合使用sigmoid激活函数;而多分类任务中,网络的最后一层使用softmax激活函数。