YOLOv4(2)-BN改进、网络感受野增强技巧、注意力机制、特征融合技巧

前言

此篇文章转载于知乎，系列文章地址：https://zhuanlan.zhihu.com/p/141533907

yolov4：YOLOv4: Optimal Speed and Accuracy of Object Detectio
论文链接：https://arxiv.org/abs/2004.10934
源码链接：https://github.com/AlexeyAB/darknet

本文分析各种BN改进、网络感受野增强技巧、注意力机制和特征融合技巧。

1 常用归一化手段

1.1 BN、GN、IN和LN

这4种归一化技术非常有名，网上分析文章非常多，故本文不打算从头到尾详细分析一遍，而是从计算角度分析4种归一化手段的计算区别。

假设输入维度是(N,C,H,W),不管哪一层归一化手段，都不会改变输出大小，即输出维度也是(N,C,H,W)。

(1) BN

对于BN，其归一化维度是N、HxW维度，故其可学习权重维度是(C,)，其实就是BN的weight和bias维度，也就是论文中的$\alpha$和$\beta$

BN本质意思就是在Batch和HxW维度进行归一化，可以看出和batch相关，如果batch比较小，那么可能统计就不准确。并且由于测试时候batch可能和训练不同，导致分布不一致，故还多了两个参数：全局统计的均值和方差值，从而eval模式是必须开的，其调用实例如下所示：

上述中C=100 其流程是：对batch输入计算均值和方差(N、H和W维度求均值)，得到维度为(C,)，然后对输入(N,C,H,W)采用计算出来的(C,)个值进行广播归一化操作，最后再乘上可学习的(C,)个权重参数即可

(2) LN

对于LN，其归一化维度是C、HxW维度或者HxW维度或者W维度，但是不可以归一化维度为H，可以设置，比较灵活，其对每个batch单独进行各自的归一化操作，归一化操作时候不考虑batch，所以可以保证训练和测试一样。 例如：

m = nn.LayerNorm(normalized_shape=[100 ,35 ,45])
input = torch.randn(20, 100, 35, 45)

如上所示，其可学习权重维度是(100,35,45)：对batch输入计算均值和方差(C、H和W维度求均值)，输出维度为(N,)，然后对输入(N,C,H,W)采用计算出来的(N,)个值进行广播归一化操作，最后再乘上可学习的(C,H,W)个权重参数即可。当然也可以设置为(35,45)，意思同样理解。

可以看出其归一化是在指定输入shape情况下的归一化，和batch无关。故可以保证训练和测试一致，不需要强制开启eval模式。

通过设置输入参数shape为(H,W),其实就是IN归一化了，比较灵活。

(3) IN

对于IN，其归一化维度最简单，就是HxW，如下所示：

输入参数必须且只能是C，其内部计算是：对batch输入计算均值和方差(H,W维度求均值方差)，输出维度为(N,C),然后对输入(N,C,H,W)采用计算出来的(N,C)个值进行广播归一化操作，最后再乘上可学习的(C,)个权重参数即可。

由于其计算均值和方差和batch没有关系，故也不需要强制开启eval模式。

(4) GN

GN是介于LN和IN之间的操作，多了一个group操作，例子如下：

注意第一个参数分组数必须能够将输入通道整除，否则会报错，因为无法均匀分组。其内部计算是：**对batch输入计算均值和方差(C/组数、H,W维度求均值方差)，输出维度为(N,组数),然后对输入(N,C,H,W)采用计算出来的(N,组数)个值进行广播归一化操作，最后再乘上可学习的(C,)个权重参数即可。**不需要强制开启eval模式。

1.2 FRN

论文名称：Filter response normalization layer: Eliminating batch dependence in the training of deep neural networks
论文链接：https://arxiv.org/pdf/1911.09737.pdf
虽然GN解决了小batch size时的问题，但在正常的batch size时，其精度依然比不上BN层。有什么办法能解决归一化既不依赖于batch，又能使精度高于BN呢？FRN就是为了解决这个问题。

要解决batch依赖问题，则不能对batch维度进行归一化。FRN层由两部分组成，Filtere Response Normalization (FRN)和Thresholded Linear Unit (TLU)。

(1) FRN

N是HxW,表面看起来计算方式非常类似IN，计算过程是：对输入的batch个样本在HxW维度上计算方差，不计算均值，得到输出维度(batch,c)，然后对(batch,c,h,w)进行除方差操作，并且引入可学习参数，权重维度是(C,),最后对上述输出乘以可学习参数即可输出。

(2) TLU
由于在FRN操作中没有减去均值，会导致“归一化”后的特征值不是关于零对称，可能会以任意的方式偏移零值。如果使用ReLU作为激活函数的话，会引起误差，产生很多零值，性能下降。所以需要对ReLU进行增强，即TLU，引入一个可学习的阈值$\tau$

从上面来看，FRN层引入了γ、β和τ三个可学习的参数，分别学习变换重构的尺度、偏移和阈值，他们都具有C个值，对应每一个通道。
一般情况下，特征图的大小N=H×W都比较大，但也有N=1的情况（全连接或者特征图为1×1）。在N=1的情况下，若ϵ很小，则会变成一个sign函数，梯度值变得很小，不利于优化；若ϵ相对较大，则曲线会平滑一点，容易优化。

故在实现方面，在N=1的情况下，将ϵ变成一个可学习的参数（初始化为10−4）；而对于N≠1时，将其固定为10−6。为了保证可学习参数ϵ>0，对其进行一定限制

其tf实现如下所示：
另外在实验上，存在几个细节：

1. 由于FRN层没有均值中心化，所以会有一些模型对初始学习率的选择十分敏感，特别是那些使用了多个最大池化层的网络。为了缓解这个问题，作者建议使用warm-up来对学习率进行调整。

2. 一般而言，FC层后一般都不会接归一化层，这是因为均值和方差计算的数量太少，难以正确估计。但如果FC层后接FRN层，性能不会下降，反而会有上升。

3. 作者对BN+TLU或者GN+TLU或者FRN+ReLU等都做过实验对比，还是发现FRN+TLU的搭配是最好。

在一些大佬实践中表明warm-up策略比较关键，如果不用效果可能不太稳定。同时整片论文都是实验性质的，没有啥原理性解释，不太好理解。而且本文看起来也蛮麻烦的，对目前的代码结构还是有蛮大的侵入性，还需要配合warm-up，用到的地方好像没有很多。

1.3 CBN

论文名称：Cross-Iiteration Batch Normalization
论文链接：https://arxiv.org/pdf/2002.05712v1.pdf
github：https://github.com/Howal/Cross-iterationBatchNorm

大家都知道当batch比较小时候，BN在batch维度统计不准确，导致准确率下降，前面的FRN也是为了解决该问题，而本文从另一个角度解决问题，思想比较make sense。在无法扩大batch训练的前提下，是否可以通过收集最近几次迭代信息来更新当前迭代时刻的均值和方差，这样就变向实现了扩大batch目的？ 但是我们知道在当前迭代时刻，参数已经更新了N次，存储的前几个迭代的参数肯定无法直接和当前迭代次数进行合并计算，也就是由于网络权重的变化，不同迭代产生的网络激活无法相互比较。故需要找到一种解决办法。所幸作者指出：由于梯度下降机制，模型训练过程中相近的几个iter所对应的模型参数的变化是平滑的（smoothly），其权重变化可以用泰勒级数拟合出来，因此通过基于泰勒多项式的拟合来补偿网络权重的变化，从而可以准确地估计统计量，并可以有效地应用批次归一化。

在训练yolo中，常用的一个技巧是设置mini batch和batch，即网络前向batch/ mini batch次，然后再进行一次梯度更新，也是为了变相扩大batch size，但是其缺点是bn操作无法实现等价的扩大N倍，本文就相当于可以解决这个问题。通常在多卡情况下一般采用SyncBN，其也叫作Cross-GPU Batch Normalization ，主要是解决batch特别小的场景，例如语义分割中batch通常都是1的情况训练效果不够好的问题，其在多个gpu上计算BN，实现了跨GPU上计算，使用多卡构造了大batch训练，属于技术改进。而本文想在单卡下实现同样效果，因为不是每个人都有多张卡。

上述图表是基于ResNet-18在ImageNet上面训练得到的top 准确率，可以看出当batch大于16后，BN的精度就蛮好了，随着batch减少，精度快速下降，GN虽然性能还可以，但是batch大的时候精度不如BN，而Naive版本的CAN效果其实和BN差不多，Naive版本是指收集最近K个迭代信息，然后用于计算当前迭代时刻的统计量，可以发现由于梯度更新原因，直接计算统计量其实没有效果，而本文的CBN可以比较好的克服。

假设当前迭代时刻为t，则$t-\tau$时刻中的统计量在t时刻的值，可以用泰勒级数近似：

$\theta$为权重参数，在第t时刻的参数${\theta }_t$，对于$t-\tau$时刻的统计值，可以在${\theta }_{t-\tau }$处展开，对于某一层l，可以进一步近似：

对于上述式子，代码就比较好写了，只要存储前k个时刻的统计量及其梯度即可。最后进行汇总就行：

注意求方差时候，采用了max操作，作者指出这样可以保留有用的统计信息(不太好理解)。得到统计量后，后面直接进行归一化即可，和标准BN计算方式一样。


上图可以很好的反映出计算过程，BN就是仅仅利用当前迭代时刻信息进行norm，而CBN在计算当前时刻统计量时候会考虑前k个时刻统计量，从而实现扩大batch size操作。同时作者指出CBN操作不会引入比较大的内存开销，训练速度不会影响很多，但是训练时候会慢一些，比GN还慢。

论文做的实验比较多，这里不详细说了，有兴趣的可以下载原文查看。有一个细节是：CBN多了一个window size，实验中设定为8。并且需要在网络训练初期要用较小的窗大小，随着网络的训练，模型参数也会越来越稳定，再用较大的窗大小可以获得更好的结果。

1.4 CmBN

CmBN是yolov4中提出的，属于CBN的小改动，但是作者论文图绘制的比较隐晦，不太好理解，本文详细说下流程。


在理解了BN流程基础上，理解CBN就非常容易了，CBN由于在计算每个迭代时刻统计量时候会考虑前3个时刻的统计量，故变相实现了大batch，然后在每个mini batch内部，都是标准的BN操作即:1 计算BN统计量;2 应用BN;3 更新可学习参数和网络权重

而CmBN的做法和前面两个都不一样，其把大batch内部的4个mini batch当做一个整体，对外隔离，主要改变在于BN层的统计量计算方面，具体流程是：假设当前是第t次迭代时刻，也是mini-batch的起点，

(1) 在第t时刻开始进行梯度累加操作

(2) 在第t时刻开始进行BN统计量汇合操作，这个就是和CBN的区别，CBN在第t时刻，也会考虑前3个时刻的统计量进行汇合，而CmBN操作不会，其仅仅在mini batch内部进行汇合操作

(3) 就是正常的应用BN，对输入进行变换输出即可

(4) 在mini batch的最后一个时刻，进行参数更新和可学习参数更新

可以明显发现CmBN是CBN的简化版本，其唯一差别就是在计算第t时刻的BN统计量时候，CBN会考虑前一个mini batch内部的统计量，而CmBN版本，所有计算都是在mini batch内部。我怀疑是为了减少内存消耗，提高训练速度，既然大家都是近似，差距应该不大，而且本身yolo训练时候，batch也不会特别小，不至于是1-2，所以CmBN的做法应该是为了yolov4专门设计的，属于实践性改进。

2 网络改进

2.1 增加感受野技巧

论文中主要是提到了三种结构：SPP层、ASPP和RFB。

(1) SPP层

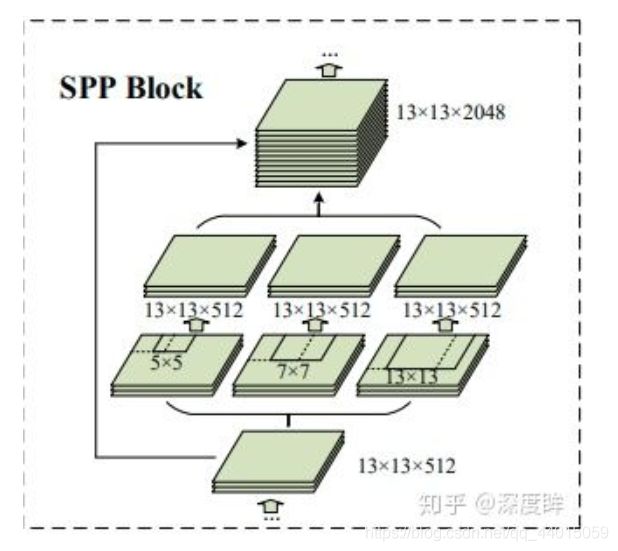
其结构如上所示，内部采用不同大小的kernel size和strdie实现不同感受野特征输出，然后concat即可，在yolov3-spp里面有具体结构：

即上一层的特征图输入是13x13x512，然后三个分支分别是stride=1，kernel size为5,9,13,然后三个图拼接，得到13x13x2048的图，然后

接一个1x1卷积，得到13x13x512的特征图，然后进行后续操作。

(2) ASPP

ASPP和SPP的差别是，并不是采用max pool得到不同感受野的特征图，而是采用卷积实现，且其kernel size全部是3，但是引入了不同的空洞率来变相扩大感受野。其余操作和SPP一致，ASPP来自DeepLab论文。

(3) RFB

RFB结构来自RFBNet，效果不错，计算量也不大，可以看出RFB是ASPP的推广，其采用了不同大小的kernel和不同的空洞率，相比ASPP，计算量减少不少，效果应该差不多RFB在推理阶段引入的计算量非常xi小，但是在ssd中AP提高蛮多，是个不错的选择。

2.2 注意力机制技巧

论文中主要是提到了SE和SAM模块

SE模块比较简单，目的是对特征通道进行重新加权，如上图所示。

SAM是CBAM论文中的空间注意力模块。其流程是：将Channel attention模块输出特征图作为本模块的输入特征图。首先做一个基于channel的global max pooling 和global average pooling，然后将这2个结果基于channel 做concat操作。然后经过一个卷积操作，降维为1个channel。再经过sigmoid生成spatial attention feature。最后将该feature和该模块的输入feature做乘法，得到最终生成的特征。

SE模块可以提升大概1%的ImageNet top-1精度，增加2%计算量，但推理时有10%的速度损失，对GPU不太友好，而SAM模块仅仅增加0.1%计算量，提升0.5%的top-1准确率，故本文选择的其实是SAM模块。

yolov4对SAM进行简单修改，如下所示：

修改spatial-wise attention 为 pointwise attention，简化了流程，目的应该也是为了提高训练速度。

2.3 特征融合技巧

特征融合，主要是指不同输出层直接的特征融合，主要包括FPN、PAN、SFAM、ASFF和BiFPN。

(1) FPN

FPN是目前最主流的不同层融合方案，应用非常广泛，其结构为：
FPN仅仅融合相邻层的特征图，采用上采样或者下采样操作得到尺度一致的特征图，然后采用add操作得到融合后特征图。

(2) PAN

PAN来自论文：Path Aggregation Network for Instance Segmentation。其结构如下所示：

FPN加入top-down的旁路连接，能给feature增加high-level语义,有利于分类。但是PAN论文作者觉得low-level的feature很有利于定位，虽然FPN中P5也间接融合了low-level的特征，但是信息流动路线太长了如红色虚线所示，其中会经过超多conv操作，本文在FPN的P2-P5又加了low-level的特征，最底层的特征流动到N2-N5只需要经过很少的层如绿色需要所示，主要目的是加速信息融合,缩短底层特征和高层特征之间的信息路径。down-top的融合做法是：

其实不管作者如何解释motivation，这种top-down和donw-top的做法，看起来也比较make sense，后面的很多FPN改进都用到了这个思想。

(3) SFAM

SFAM来自M2det: A single-shot object detector based on multi-level feature pyramid network

其中SFAM结构如下所示：

SFAM全称是Scale-wise Feature Aggregation Module，不同尺度的特征进行重组和融合，基本原理是对不同TUM的输出（每个TUM有6个不同尺度的输出），将其中相同尺度的特征进行concat，然后经过一个SE模块（对通道进行reweighting）输出，然后进行检测。其实就是把相同尺度的各层金字塔特征提取出来，然后concat，经过se模块，进行通道加权，再进行后续的预测，实现对不同通道进行不同加权功能。看起来开销有点大呀，因为要多个stage。

和FPN及其改进版本的不同是SFAM的融合是尺度感知的，只融合相同尺度的特征，而不是像FPN那样，强制上下采样然后进行融合。

(4) ASFF

ASFF来自论文：Learning Spatial Fusion for Single-Shot Object Detection，也就是著名的yolov3-asff,

FPN操作是一个非常常用的用于对付大小尺寸物体检测的办法，作者指出FPN的缺点是不同尺度之间存在语义gap，举例来说基于iou准则，某个gt bbox只会分配到某一个特定层，而其余层级对应区域会认为是背景(但是其余层学习出来的语义特征其实也是连续相似的，并不是完全不能用的)，如果图像中包含大小对象，则不同级别的特征之间的冲突往往会占据要素金字塔的主要部分，这种不一致会干扰训练期间的梯度计算，并降低特征金字塔的有效性。一句话就是：目前这种concat或者add的融合方式不够科学。本文觉得应该自适应融合，自动找出最合适的融合特征, 简要思想就是：原来的FPN add方式现在变成了add基础上多了一个可学习系数，该参数是自动学习的，可以实现自适应融合效果，类似于全连接参数。 ASFF具体操作包括 identically rescaling和adaptively fusing。

定义FPN层级为l，为了进行融合，对于不同层级的特征都要进行上采样或者下采样操作，用于得到同等空间大小的特征图，上采样操作是1x1卷积进行通道压缩，然后双线性插值得到；下采样操作是对于1/2特征图是采样3 × 3 convolution layer with a stride of 2，对于1/4特征图是add a 2-stride max pooling layer然后引用stride 卷积。其自适应融合过程如下：

具体操作为：

(1) 首先对于第l级特征图输出cxhxw，对其余特征图进行上下采样操作，得到同样大小和channel的特征图，方便后续融合

(2) 对处理后的3个层级特征图输出，输入到1x1xn的卷积中(n是预先设定的)，得到3个空间权重向量，每个大小是nxhxw

(3) 然后通道方向拼接得到3nxhxw的权重融合图

(4) 为了得到通道为3的权重图，对上述特征图采用1x1x3的卷积，得到3xhxw的权重向量

(5) 在通道方向softmax操作，进行归一化，将3个向量乘加到3个特征图上面，得到融合后的cxhxw特征图

(6) 采用3x3卷积得到输出通道为256的预测输出层

(5) BIFPN

BiFPN来自论文：EfficientDet: Scalable and efficient object detection 。ASFF思想和BiFPN非常类似，也是可学习参数的自适应加权融合，但是比ASFF更加复杂。

思想都差不多，多尺度融合不仅仅是从下到上，也要从上到下，并且融合的参数都是学习出来的，不是简单的add或者concat就Ok的。