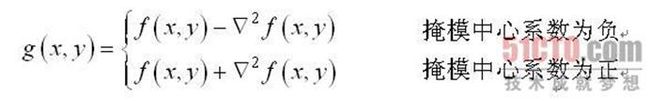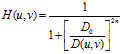图像增强技术基础、评价指标及其经典算法
声明
1）本文仅供学术交流，非商用。具体引用的资料请看参考文献。如果某部分不小心侵犯了大家的利益，请联系博主删除。
2）本人才疏学浅，整理总结的时候难免出错，还望各位前辈不吝指正，谢谢。
联系方式：[email protected]
图像增强技术基础及其经典算法
第一章 图像的基础知识
1.图像信号的基本概念
1.1. 数字图像的基本类型
1.1.1位图
位图是使用二维像素矩阵来表示的图像，每个像素的亮度信息或者颜色信息用灰度或RGB分量表示。每一个像素值所占的比特位可以是1、4、8、16、24、位等，位数越高所包含的信息就越丰富。与其不同的是矢量图。
1.1. 2.二值图像
二值图像有黑白两种颜色构成，也叫黑白图像，其图像像素值只有0和1两个值。
1.1.3.灰度图像
二值图像是一种灰度图像的特殊情况。灰度图像在黑色和变色之间加入了2g-2个颜色深度（g表示比特位数）。
1.1.4.索引图像
索引图像世界上就是把像素的值作为颜色的索引序号，可以根据这个序号能找到该像素对应的实际颜色。同时可以根据需要定义很多索引图像，常用的有热金属色、伪彩图像等。s
1.1.5.RGB彩色图像
自然界中几乎所有的颜色都可以有三原色（RGB）组合而成，RGB图像应用了这一原理。RGB图像有红绿蓝三个分量组成，一般的RGB图像像素每个颜色分量8位，共24位，理论上行可以合成224中不同的颜色。
1.2. 图像的彩色模型
①RGB——加色混合色彩模型
②CMY——减色混合色彩模型
③YUV模型和YIQ模型——应用于电视传播系统的色彩模型
④YCbCr颜色空间
⑤HIS——数据额色彩模型
1.3. 图像的分辨率
①空间分辨率：图像的大小
②灰度级分辨率：每个像素所占的位数
2.人眼的视觉原理
2.1相对视敏度
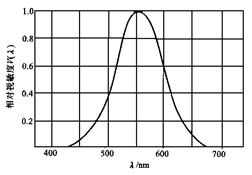
人眼对辐射功率相同而波段不同的光产生的亮度感觉不同。感觉最亮的是黄绿色（波长为555nm），下图为白天正常光照下的相对视敏度曲线
2.2明暗视觉
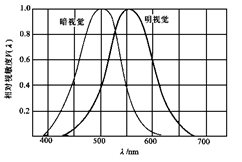
不同亮度下，人眼的视敏度曲线会发生变化。弱光条件下，视敏度曲线会向左移。
2.3对比灵敏度
研究表明，人眼刚能分辨的强度差ΔI是背景I的函数，有时采用相对辨别门限ΔI/I或称之韦伯比（Weber Ratio）来表示辨别情况。ΔI/I在相当宽的强度范围内近似为常数，约等于0.02，但当照明强度过高或过低时则不成立。图2 给出了韦伯比与照明强度的关系。由于人眼的韦伯比的作用，加之当人眼适应了某种恒定的背景亮度后，对黑白的感觉范围相应缩小，所以人眼对高亮度背景和低亮度背景中的图像细节的敏感度比较低，而对中亮度背景中的图像细节的敏感度比较高。因此，可以根据人眼的视觉特性对灰度图像的直方图进行改进，将图像的灰度调整到人眼视觉观察的最佳范围，从而使图像更有利于人眼的观察和识别。
2.4可见度阈值和马赫带消影
可见度阈值时指人眼刚好能识别的干扰值，低于该阈值的干扰值就是觉察不来的。
所谓"马赫带效应（Mach band effect）"是指视觉的主观感受在亮度有变化的地方出现虚幻的明亮或黑暗的条纹，马赫带效应的出现是人类的视觉系统造成的。生理学对马赫带效应的解释是：人类的视觉系统有增强边缘对比度的机制。
2.5图像质量的评估标准与方法
2.5.1主观评价
主观直接反应人眼的感觉。
2.5.2客观评价
通过计算恢复图像偏离原始图像的误差来衡量恢复图像的质量，最常用的有均方误差和峰值信噪比：
（n代表像素的位数）
第二章 常用图像增强技术
1.空域图像增强
1.1灰度变换
空域增强方法可表示为
表示增强后的图像，表示增强前的图像；表示增强操作。若是定义在每个上的，是点操作。常见的变换有：
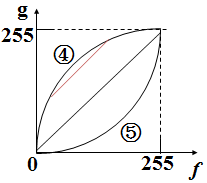
1.1.1线性变换
1.1.2非线性变换（对数变换、幂次变换等）
1.2直方图（Histogram）均衡
直方图均衡以概率统计为基础进行增强处理。以横轴表示直方图的灰度级，纵轴表示对应灰度级的像素个数，就可得到图像的直方图，直方图提供了原图的灰度值分布情况和整体描述；通过改变直方图的形状可以达到增强图像对比度的效果。
基于直方图的灰度变换,是调整图像直方图到一个预定的形状。例如,一些图像由于其灰度分布集中在较窄的区间，对比度很弱,图像细节看不清楚。如：
此时,可采用图像灰度直方图均衡化处理,使得图像的灰度分布趋向均匀,图像所占有的象素灰度间距拉开,加大图像反差，改善视觉效果,达到增强目的。增强后的图像如下：
直方图灰度变换后，直方图占据整个图像灰度值的允许范围，增加了图像的动态范围，细节清楚了。
直方图均匀化处理的思路：
①将原始图像灰度级归一化在之间，即；
②设
为原始图像灰度分布的概率密度函数,
直方图均匀化处理实际上就是寻找一个灰度变换函数
，使变化后的灰度值
，且归一化为
；
再建立原象素
与新象素
之间的映射关系；
主要是要求处理后图像灰度分布的概率密度函数均为
，即期望所有灰度级出现概率相同。累计分布函数是常用的均衡化函数。
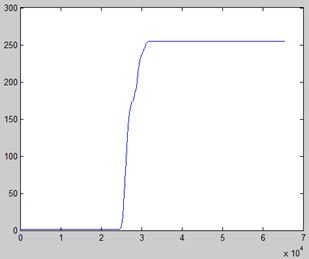
累计分布函数能作为直方图均衡的原因：假设下图是一个640×480图像的累计分布函数曲线。该曲线的低像素值和高像素值数量较少，所以曲线的两端较为平坦；而在中间灰度值的像素较多，所以曲线较为陡峭。基于此，直方图均衡后应该能使中间值的像素被拉伸，其它灰度值的像素被压缩。而图中的累计分布函数曲线恰好可以实现这一点。
例子：
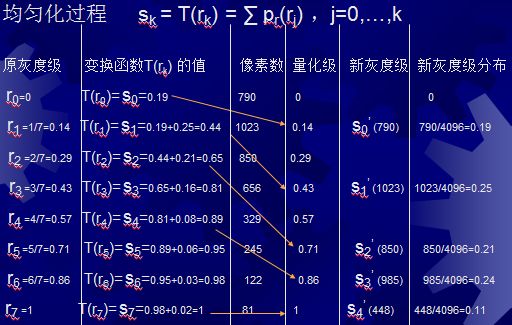
设一幅图像64*64=4096个像素(即N=4096)，共有8个灰度级(0-7)，采用累计分布函数均衡化灰度级。
分布情况如下：
| 灰度级 |
r0=0 |
r1 =1/7 |
r2 =2/7 |
r3 =3/7 |
r4 =4/7 |
r5 =5/7 |
r6 =6/7 |
r7 =1 |
| 像素数 |
790 |
1023 |
850 |
656 |
329 |
245 |
122 |
81 |
| 概率 |
0.19 |
0.25 |
0.21 |
0.16 |
0.08 |
0.06 |
0.03 |
0.02 |
计算新的图像：
1.3空域滤波
1.3.1邻域均值滤波
用于平滑噪声，但在边缘区域会造成模糊效应。
1.3.2中值滤波
中值滤波是基于统计排序，在平滑噪声时对边缘区域的保持效果要优于邻域均值法，但计算时间较长。
1.3.3拉普拉斯模板
拉普拉斯模板主要用于图像锐化，缺点是对噪声比较敏感。
拉普拉斯算子是最简单的各向同性微分算子，具有旋转不变性。一个二维图像函数 的拉普拉斯变换是各向同性的二阶导数，定义为：
为了更适合于数字图像处理，将该方程表示为离散形式：
另外，拉普拉斯算子还可以表示成模板的形式，如下图所示。（a）表示离散拉普拉斯算子的模板，（b）表示其扩展模板，（c）则分别表示其他两种拉普拉斯的实现模板。从模板形式容易看出，如果在图像中一个较暗的区域中出现了一个亮点，那么用拉普拉斯运算就会使这个亮点变得更亮。因为图像中的边缘就是那些灰度发生跳变的区域，所以拉普拉斯锐化模板在边缘检测中很有用。一般增强技术对于陡峭的边缘和缓慢变化的边缘很难确定其边缘线的位置。但此算子却可用二次微分正峰和负峰之间的过零点来确定，对孤立点或端点更为敏感，因此特别适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。同梯度算子一样，拉普拉斯算子也会增强图像中的噪声，有时用拉普拉斯算子进行边缘检测时，可将图像先进行平滑处理。
图像处理中的拉普拉斯算子
图像锐化处理的作用是使灰度反差增强，从而使模糊图像变得更加清晰。图像模糊的实质就是图像受到平均运算或积分运算，因此可以对图像进行逆运算，如微分运算能够突出图像细节，使图像变得更为清晰。由于拉普拉斯是一种微分算子，它的应用可增强图像中灰度突变的区域，减弱灰度的缓慢变化区域。因此，锐化处理可选择拉普拉斯算子对原图像进行处理，产生描述灰度突变的图像，再将拉普拉斯图像与原始图像叠加而产生锐化图像。拉普拉斯锐化的基本方法可以由下式表示：
这种简单的锐化方法既可以产生拉普拉斯锐化处理的效果，同时又能保留背景信息，将原始图像叠加到拉普拉斯变换的处理结果中去，可以使图像中的各灰度值得到保留，使灰度突变处的对比度得到增强，最终结果是在保留图像背景的前提下，突现出图像中小的细节信息。
2.频域图像增强
2.1理想低通滤波器ILPF（Idea Low-Pass Filter）
传递函数：
式中，D0是一个规定的非负量，理想低通滤波器的截止频率；
代表从频率平面的原点到
点的距离，
2.2巴特沃思低通滤波器BLPF（Butterworth Low-Pass Filter）
传递函数（n阶）: 
，
H(u,v)降到1/2时取为截止频率D0。
2.3高斯低通滤波器
与巴特沃思低通滤波器一样，高斯低通滤波器也能避免振铃效应。
2.4 Butterworth高通滤波器BHPF
3.图像客观评价指标
3.1人眼视觉系统
①人眼分辨细节的能力与相对亮度成正比，而不是取决于整体亮度，这也是韦伯定律的基础，因此相对于平坦区域，人眼对图像边缘轮廓新的失真更加敏感。
②人眼对图像细节的铭感度与其背景的亮度有关，对中高亮度背景情况下的细节信息较敏感，对低亮度和高亮度背景下的细节敏感度则较低。
③人眼对低频下的噪声敏感度要高于高频区域，即人眼更容易感知平坦区域的噪声，而不是边缘区域的噪声。
3.2归一化灰度差
归一化灰度差NID用来描述绝对亮度值与视频图像质量的关系：
为人眼视觉的最佳平均灰度值127，为视频图像的灰度均值。
3.3归一化对比度
分别是第个图像分块上的最大值和最小值，为视频图像分块个数。
3.4归一化信息熵
式中表示概率分布密度，当时，零。显然，均有均匀分布直方图的图像具有最大的信息熵，仅有一个灰度值的图像的信息熵最小。因此归一化的信息上NE表示为+
3.5综合图像质量
越大表示图像质量越好。