深度学习——一些零零散散的知识点（边学边更新）

本文用于记录一些在学习当中遇到的零散知识点或一些比较有意思的想法。

1. 卷积神经网络

1.1 Pooling层

原文

图中红点表示特征响应，个人理解是其四周可较大程度代表图像；蓝色表示卷积核。图（2）因为卷积核尺寸较小，不能捕捉到复杂信息（同时囊括两个红点），尽管在卷积核平移后可以捕捉另外一个特征响应点，但丧失了A，B两特征的空间关系。要么增大卷积核的尺寸（会增加参数量），要么下采样，缩小特征响应间距离。
随着网络加深，特征的尺寸和它们之间的空间关系会增长。如果此时大多数特征的空间关系都超过了卷积核大小，那么卷积核将无法再捕捉到任何复杂信息。

1.2 感受野——RF

参考CSDN
参考知乎

Receptive Field Size，通常指feature map上的一个像素点能对应原始输入图像多大区域。

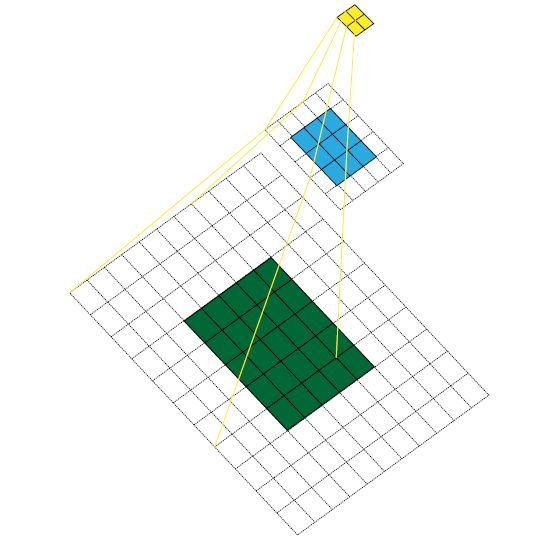
所谓感受野就是黄色图像的一个像素点，所对应的绿色图像的区域。途中第一层卷积的感受野是3，第二层是7。

感受野计算

以下k代表卷积核大小；s代表步长；p代表padding

感受野的计算是基于卷积核卷积的公式$$Out=\frac{Input+2p-k}{s}+1$$其逆公式为$$Input=(Out-1)\ast s+k-2p$$计算感受野时，采取自顶向下的策略，从输出层反向推导一个点相对于输入层的RF。

所有点分为两种，在边缘和不在边缘，两种分开考虑

1. 非边缘点

由于点不在边缘，所以其感受的范围与padding无关。因此$$R{f}_i=(R{f}_{i+1}-1)\ast s+k$$这是由卷积的逆公式演变来的。例图中，黄色为$R{f}_{i+1}$时， 蓝色为$R{f}_i$。

2. 边缘点

边缘点实际感受到的范围里不应该包括padding部分，因而$$R{f}_i=(R{f}_{i+1}-1)\ast s+k-p$$

在计算某一层的感受野时，只需将其看作输出层，并置其$Rf=1$，然后向输入层逐层迭代，最后得到的值即是感受野大小。

1.3 学习能力

原文
结合1.1和1.2，引入一个概念——学习能力，指卷积核学习复杂特征如空间特征的能力。在满足两种条件同时使模型层数最大化即可得到最有效果。其中之一的条件就是学习能力。

1.3.1 第一个约束条件

为了定量分析卷积核学习能力的大小，定义c-value$$c-value=\frac{RealFilterSize}{ReceptiveFieldSize}$$

Real Filter Size

对于一个k * k大小的卷积核来说，在没有下采样时其值为k。每经过一次下采样，值都会改变。

Receptive Filter Size

这里的RF计算方式与1.2中提到的稍微不同，这里为了简化计算，在最后得出感受野时减了1。

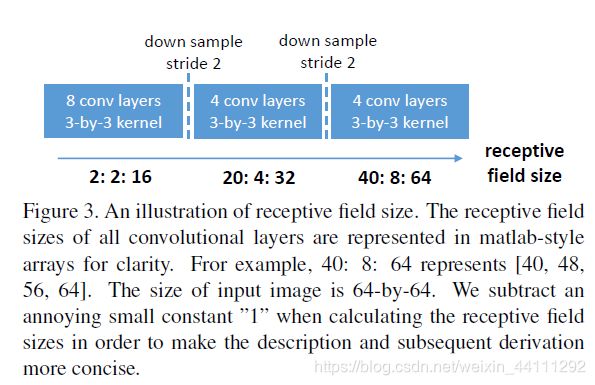
譬如上图卷积十次后的大小：
$10:1$
$9:3=(1-1)\ast 2+3$
$8:5=(3-1)\ast 1+3$
$7:7=(5-1)\ast 1+3$
$6:9=(7-1)\ast 1+3$
$5:11=(9-1)\ast 1+3$
$4:13=(11-1)\ast 1+3$
$3:15=(13-1)\ast 1+3$
$2:17=(15-1)\ast 1+3$
$1:19=(17-1)\ast 1+3$
$Rf:20=(19-1)\ast 1+3-1$

这样定义提出第一个条件：每个卷积层的c-value都应该大于最小值t（学习能力应具有最小值），使模型顶层的RF足够大。根据经验发现，t=1/6对于不同任务的所有卷积层是一个很好的c-value下界。

1.3.2 第二个约束条件

第二个约束条件称作学习的必要性。随着RF的不断增大，越来越复杂的特征开始出现（多种特征组合），在这个过程中需要添加额外的层来学习新出现的特征。当RF达到整个输入图像大小时表明已经涵盖了图像所有的特征，此时应当停止学习新的特征，以避免过拟合。
因此第二个约束条件就是，输出层RF的尺寸不能大于图像的尺寸。

• 如此一来，两条约束条件总体表达的是：模型顶层RF不能大于输入图像尺寸且应足够接近输入尺寸

1.4 深度模型的设计思路

在这部分将深层架构的设计转换为约束最优化问题，然后给出在一定条件下的最优解。此处假设每一层的卷积核大小相同，且不考虑卷积核的个数，因为卷积核个数依赖于实际问题。

1.4.1 深度卷积网络结构

首先定义一些参数

• z: 图像尺寸
• k: 卷积核尺寸
• t: 最小c-value

深层模型架构由n个stage和每个stage中$ai$层个数决定，且每个stage由一次下采样分隔。例如n = 3, a1 = 2, a2 = 6, a3 = 4表示有3个模块，每个模块中分别含2层，6层和4层网络。深度学习的目标本质上是最大化层数

1.4.2 第一个约束条件

同一stage中，最后一层的c-value值是最小的，因此条件等价于每一个stage中的最后一层的c-value不能小于t。$$\frac{2^{l}k}{{\sum }_{i=1}^l{2}_{i-1}(k-1)a_i}>=t,wherel=1,2,...,n$$
分子是第$l$个stage的real filter size， 分母是第$l$个stage的最后一层的RF。

1.4.3 第二个约束条件

最顶层的RF不能大于输入尺寸$$\sum _{i=1}^l{2}_{i-1}(k-1)a_i<=z$$左式为最顶层卷积层的RF

1.4.4 网络层数最优解

在1.4.2和1.4.3两个约束条件下最大化层数得到最优化问题
$$n,a_i=argmax\sum _i^n{a}_i$$s.t.
$$\sum _{i=1}^l{a}_i{2}^{i-1}<=\frac{2^{l}k}{t(k-1)},wherel=1,2,...,n$$
$$\sum _i{a}_i{2}^{i-1}<=\frac{z}{k-1}$$

假设图像尺寸为$z=\frac{2^{m-1}k}{t}$，层数$ai$为正实数，则最优解为$$n=m$$
$$a_1=\frac{k}{(k-1)t},a_2=...=a_n=\frac{1}{2a_1}$$

• 设计深层架构时

1. 指导我们在输入参数给定的条件下怎么选择降采样次数，（n=m）
2. 除了第一个stage外，其他stage的层数要尽可能的均匀分布
3. 给出了一系列不同尺寸卷积核能达到的最大深度，基于此我们可以更好的权衡卷积核的尺寸。

1.5 通道叠加

有时可能需要改变图片的通道。将多通道降维容易理解，但是在一些场景中，可能需要将单通道的数据转为多通道。例如MNIST数据集（灰度图像），或者本来不是图像的二维矩阵做卷积使用现成模型时也会遇到这样的问题

解决办法也很简单

from PIL import Image

sample = ...   # sample是np.ndarray格式
sample = Image.fromarray(sample)
sample = sample.convert('RGB')

这样sample 就变成目标的三通道了

2. 训练

2.1 修改学习率

修改学习率，使得每次梯度下降低于某个值或停止下降时，降低学习率，来使得梯度进一步下降。

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)  # 优化器
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)  # 设定优优化器更新的时刻表

def train(...):
    for i, data in enumerate(train_loader):     
        ......
        y_ = model(x)   
        loss = criterion(y_,y)     
		optimizer.zero_grad()     
        loss.backward()             
        optimizer.step()            
        ......
 # 开始训练
for epoch in range(epochs):
    train(...)
    veritf(...)
    scheduler.step()        #每轮epoch更新学习率

参数解释：

• step_size: 更新步长
• gamma: 学习率衰减速率，默认0.1

假设初始lr = 0.5, step_size = 20, gamma = 0.1

epoch = 1时，lr = 0.5
epoch = 5时，lr = 0.5
epoch = 20时，lr=0.05
epoch = 40时，lr=0.005

即每step_size个epoch，lr更新为原始的gamma倍

2.2 使用迁移学习

进行迁移学习可有效提高准确率。

在paddlepaddle的猫十二分类比赛中，如果从头开始训练ResNet50，准确率最高只能到0.3；
而在进行迁移学习调用预训练模型，在其基础上进行微调可使准确率飙升到0.94，且训练时间和epoch巨幅减小。

2.3 训练函数格式

1. 每个epoch中先后进行train和val阶段
2. 每个epoch中根据验证集准确率不断更新最优模型参数，最终返回最优模型参数而非模型

大致流程

def train():
	best_model_wts = copy.deepcopy(model.state_dict())
	best_acc = 0.0
	
	for epoch in range(epochs):
		
		for phase in ['train', 'val']:
			if phase == 'train':
				model.train()
			else:
				# 验证集不参与权重运算
				model.eval()
			
			...
		# 最终得到了一组best_acc和 best_wts
		if phase == 'val' and epoch_acc > best_acc:
			best_acc = epoch_acc
			best_model_wts = copy.deepcopy(model.state_dict())

这种train格式的示例代码

2.4 模型保存

将训练出的模型参数保存，在使用时直接调用

2.4.1 深度学习模型保存

• 保存时

model = ...

torch.save(model.state_dict(), model_path)

• 调用时

model = ...
model.load_state_dict(torch.load(model_path))

2.4.2 传统机器学习模型保存

• 保存时

import pickle

with open(model_path, 'wb') as f:
	pickle.dump(model, f)

• 调用时

with open(model_path, 'rb') as f:
	model = pickle.load(f)

3. NLP

3.1 词向量

一句话用向量编码表示第一时间想到的是one-hot编码。好处是无论是什么字都能用一个一维数组用01表示，且不同字的向量不会重复，表达本征的能力极强。但是这也引出了one-hot向量的弊端：无法表达关联特征0——任何两个特征之间的相关性为0。

比如将“心脏病”和“胃病”做ont - hot向量

心脏病  [0， 1]
胃   病   [1， 0]

这样标记心脏病和胃病毫无关联，无法正确反映关联关系。但如果这样表示

				天气影响		心情影响		压力       生活作息
心脏病		[   0.7                0.9           0.6              0.3        ]
胃   病   	[   0.1                0.7           0.3              0.9        ]

（瞎编的）这样可以反应二者的关联关系。如此一来，引入embedding机制

Embedding向量化

Embedding解决了one-hot向量特征之间无任何关联的问题，将稀疏的特征矩阵通过cnn全连接等操作（统称查表）转为密集矩阵表示词向量。
为了实现密集矩阵，我们需要

1. 将一句话转换成向量
2. 需要一个初始的可以更新的特征编码矩阵

Embedding解决的就是第二个问题。 具体实现方法可以概括为

1. 先将文字转换成普通的整数编码
2. 用Embedding进行可更新的向量编码
3. 利用data更新

使用Embedding可以解决的有：升维和降维。

• 降维：将稀疏矩阵降维
• 升维：将笼统的特征分开

---

奇葩问题合集

记录一些让我抓狂一度骂街的问题。

1. 释放显存

当使用VSC调用cuda训练模型时，假如训练异常终止，会出现cuda内存满了的情况。即使关掉了VSC也无法释放显存。

1. 打开cmd， 键入tasklist
   
2. 找到code.exe，通常会连着出现。
   
3. 键入taskkill /pid 进程号，杀死进程。注意，进程号必须是所有code.exe中最上面的那个
   

2. num_workers

在使用torch.utils.data.DataLoader时，若将其参数num_workers设置为非零时，训练根本跑不动——连第一个epoch都不让你进。

如果还是想使用num_workers多线程训练，尝试将代码，尤其是train()部分代码封装到if __name__ == '__main__':中