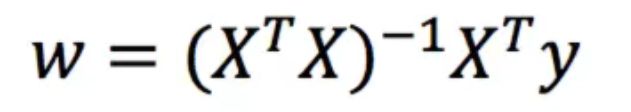机器学习入门篇（二）

一、sklearn 转换器和估计器

1.1 转换器 – 特征工程的父类

1. 实例化（实例化的是一个转换器类（Transformer））
2. 调用 fit_transform()
   标准化：(x - mean) / std

fit_transform()
		fit()   计算每一列的平均值、标准差
		transform()  (x - mean) / std

1.2 估算器 – sklearn机器学习算法的实现

1. 实例化一个estimator
2. estimator.fit(x_train, y_train) 计算 模型生成
3. 模型评估

1. 直接比对真实值和预测值
y_predict = estimator.predict（x_test）
y_test  == y_predict
2.计算准确率
accuracy = estimator.score(x_test, y_test)

二、KNN算法

KNN（K Nearest Neighbor）算法是机器学习中比较经典的算法。如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。.

如何确定距离？

k值不易取过大，因为会受到样本不均衡的影响。
k值过小，容易受到异常点的影响。

鸢尾花种类预测案例

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
# 1.获取数据集
datas = load_iris()
# 2.划分数据集
x_train, x_test, y_train, y_test = train_test_split(datas.data, datas.target, test_size=0.2)
# 3.特征工程：标准化
transfer = StandardScaler()
x_train_st = transfer.fit_transform(x_train)
x_test_st = transfer.transform(x_test)
# 4.KNN算法预估器 生成模型
estimator = KNeighborsClassifier(n_neighbors=3)
estimator.fit(x_train_st, y_train)
# 5.模型评估
y_predict = estimator.predict(x_test_st)
print("预测值：", y_predict)
print("比对真实值和预测值：", y_predict == y_test)
score = estimator.score(x_test_st, y_test)
print("准确率为：", score)

预测值： [2 2 1 1 0 1 1 0 2 2 0 0 0 0 2 0 0 2 1 0 2 0 2 0 0 2 1 1 2 2]
比对真实值和预测值： [ True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True False  True  True False  True  True  True
  True  True  True  True  True  True]
准确率为： 0.9333333333333333

2.1 K-近邻算法总结

优点：简单，易于理解，易于实现，无需训练
缺点：
懒惰算法，对测试样本分类时的计算量大。内存开销大
必须指定K值，K值选择不当则分类精度不能保证
使用场景：小数据场景，几千~几万样本，具体场景具体业务去测试

2.2 模型选择与调优

该节是为了解决k值手动选择不当而导致分类精度不够。

2.2.1 交叉验证（cross validation）

交叉验证：将拿到的训练数据，分为训练和验证集。以下图为例：将数据分成4份，其中一份作为验证集。然后经过4次（组）的测试，每次都更换不同的验证集。即得到4组模型的结果，取平均值作为最终结果。又称4折交叉验证。

为什么要用交叉验证？

1. 减少过拟合现象，提高泛化能力。如果我们用全部的数据集作为训练数据进行建模，训练出来的模型很有可能对训练数据有较强的依赖性，即对训练数据的结果准确度很高，而对外来其他数据准确度较差。
2. 提高数据的使用价值。从有限数据中获取尽可能多的有效信息。将数据进行不同程度的拆分再组合，可以从不同较度发掘数据中隐含的信息或价值。

2.2.2 超参数搜索-网格搜索(Grid Search)

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

案例：鸢尾花分类

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
# 1.获取数据集
datas = load_iris()
# 2.划分数据集  （x_train 训练集特征值）(x_test 测试集特征值) (y_train 训练集目标值) (y_test 测试集目标值)
x_train, x_test, y_train, y_test = train_test_split(datas.data, datas.target, test_size=0.2)
# 3.特征工程：标准化
transfer = StandardScaler()
x_train_st = transfer.fit_transform(x_train)
x_test_st = transfer.transform(x_test)
# 4.KNN算法预估器
estimator = KNeighborsClassifier()
# 5.添加网格搜索和交叉验证
param_dict = {"n_neighbors": [1, 3, 5, 7, 9, 11]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10)
# 6.训练
estimator.fit(x_train_st, y_train)
# 7.模型评估
# 方法一：比对预测值和真实值
y_predict = estimator.predict(x_test_st)
print("预测值：", y_predict)
print("比对真实值和预测值：", y_predict == y_test)
# 方法二：计算准确率
score = estimator.score(x_test_st, y_test)
print("准确率为：", score)

# 最佳参数
print("最佳参数:\n", estimator.best_params_)

# 最佳结果
print("最佳结果：\n", estimator.best_score_)

# 最佳估计器
print("最佳估计器：\n", estimator.best_estimator_)

# 交叉验证结果
print("交叉验证结果：\n", estimator.cv_results_)

E:\anaconda3\envs\env_one\python.exe F:/PycharmProjects/machineLearning/knn_iris_cvgs.py
预测值： [2 1 0 2 0 0 2 0 0 0 1 2 0 0 1 1 1 0 0 1 0 1 2 2 1 2 2 2 1 0]
比对真实值和预测值： [ True  True  True  True  True  True False  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True]
准确率为： 0.9666666666666667
最佳参数:
 {'n_neighbors': 5}
最佳结果：
 0.9499999999999998
最佳估计器：
 KNeighborsClassifier()

三、朴素贝叶斯

• 联合概率：包含多个条件，且所有条件同时成立的概率，记作：P(AB) 或者 P(A,B)。
• 条件概率：事件A在另外一个事件B已经发生条件下的发生概率。记作：P(A|B)。
• 相互独立：如果P(A,B) = P(A|B)，则称事件A与事件B相互独立。
• 朴素贝叶斯：假设特征与特征之间相互独立。
  

from sklearn.naive_bayes import MultinomialNB
# 用朴素贝叶斯算法对新闻进行分类
def classify_news():
    # 1. 获取数据集
    datas = fetch_20newsgroups(subset="all")
    # 2. 划分数据集（训练集特征值，测试集特征值，训练集目标值，测试集目标值）
    x_train, x_test, y_train, y_test = train_test_split(datas.data, datas.target, test_size=0.2)
    # 3. 特征工程 训练集特征值 测试集特征值
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 4. 朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train, y_train)
    # 5. 模型评估
    # 方法一：比对预测值和真实值
    y_predict = estimator.predict(x_test)
    print("预测值：", y_predict)
    print("比对真实值和预测值：", y_predict == y_test)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：", score)

预测值： [ 7  7  4 ... 15  5  5]
比对真实值和预测值： [ True  True  True ...  True  True  True]
准确率为： 0.8413793103448276

四、决策树

消除随机性不定性
决策树的划分依据 – 信息增益

from sklearn.tree import DecisionTreeClassifier
# 决策树对鸢尾花进行分类
def decision_tree():
    # 1.获取数据集
    iris = load_iris()
    # 2.划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2)
    # 3.决策器预估器
    estimator = DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train, y_train)
    # 4. 模型评估
    # 方法一：比对预测值和真实值
    y_predict = estimator.predict(x_test)
    print("预测值：", y_predict)
    print("比对真实值和预测值：", y_predict == y_test)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：", score)
	
	# 可视化决策树
    export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)

五、随机森林

集成学习通过建立多个模型组合来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和做出预测，这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。在机器学习中，随机森林是一个包含多个决策树的分类器。

六、线性回归

回归问题：目标值 —> 连续型的数据

6.1 线性回归原理

线性回归（Linear Regression）是利用回归方程（函数）对一个或多个自变量（特征值）和因变量（目标值）之间关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，多一个自变量情况的叫做多元回归。

变量 x1、x2… 表示特征值
系数 w1、w2… 表示权重值
h(w) 表示目标值

线性回归当中线性模型有两种，一种是线性关系，另一种是非线性关系。

• 单个特征
  
• 多个特征

注：单特征与目标值的关系呈直线关系，两个特征与目标值呈现平面的关系。

线性模型：
① 自变量一次
y = w1x1 + w2x2 + w3x3 + w4x4 + .... + b
② 参数一次
y = w1 + w2x1^2 + w3x2^2 + .... + b

• 非线性关系
  

6.2 损失函数

• y1 、y2、y3、、、yt 为第 t 个样本真实值
• h(x1)、h(x2)、、、h(xt) 为第 t 个样本预测值
• 又称最小二乘法

6.3 优化算法

如何去求解模型中的w，使得损失最小。
线性回归经常使用的两种优化算法

• 正规方程
  
  X 为特征值矩阵，y 为目标值矩阵
  缺点：当特征过多过复杂时，求解速度太慢。

• 梯度下降（Gradient Descent）
  通过迭代找出最小w

6.4 案例–波士顿房价预测

from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.datasets import load_boston
# 正规方程对波士顿房价进行预测
def linear():
    # 1. 获取数据集
    boston_data = load_boston()
    # 2. 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston_data.data, boston_data.target, random_state=22)
    # 3. 标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 4. 预估器
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)
    # 5. 得出模型
    print("权重系数为：", estimator.coef_)
    print("偏置为：", estimator.intercept_)


# 梯度下降对波士顿房价进行预测
def gradient_descent():
    # 1. 获取数据集
    boston_data = load_boston()
    # 2. 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston_data.data, boston_data.target, random_state=22)
    # 3. 标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 4. 预估器
    estimator = SGDRegressor()
    estimator.fit(x_train, y_train)
    # 5. 得出模型
    print("权重系数为：", estimator.coef_)
    print("偏置为：", estimator.intercept_)

权重系数为： [-0.64817766  1.14673408 -0.05949444  0.74216553 -1.95515269  2.70902585
 -0.07737374 -3.29889391  2.50267196 -1.85679269 -1.75044624  0.87341624
 -3.91336869]
偏置为： 22.62137203166228
权重系数为： [-0.423271    0.77022841 -0.5125141   0.80851028 -1.40961105  2.88293746
 -0.12732762 -2.7884249   1.34538988 -0.67604998 -1.67337719  0.87275526
 -3.90637954]
偏置为： [22.63577162]

6.5 回归性能评估

均方误差（Mean Squared Error）评价机制：

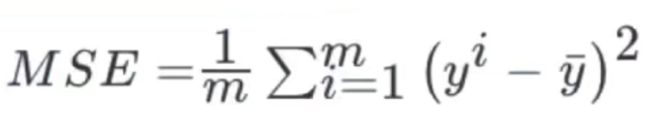
第一个参数为预测值，第二个参数为真实值

from sklearn.metrics import mean_squared_error
# 6. 模型评估
y_predict = estimator.predict(x_test)
print("预测房价：", y_predict)
error = mean_squared_error(y_test, y_predict)
print("正规方程均方误差：", error)
# 正规方程均方误差： 20.627513763095408

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度O(n^3)

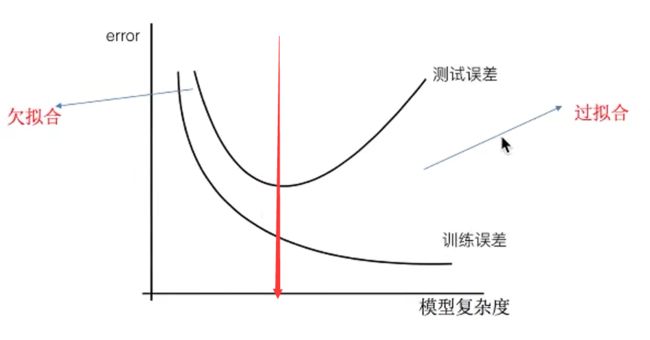
七、欠拟合与过拟合

问题：训练数据训练的很好啊，误差也不大，为什么在测试集上面有问题呢？

• 泛化能力：机器学习方法训练出来一个模型，对于已知的数据(训练集)性能表现良好，对于未知的数据(测试集)也应该表现良好的机器能力。

• 欠拟合（underfitting）

机器学习学习到的天鹅特征太少了，导致区分标准太粗糙，不能准确识别出天鹅。

• 过拟合（overfitting）

机器学习学习到天鹅特征是白色的，等到测试就会认为黑色天鹅不是天鹅。

• 过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。（模型过于复杂）

• 欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。（模型过于简单）

八、岭回归

岭回归，其实是一种线性回归。只不过是在算法建立回归方程时候，加上正则化的限制，从而达到解决过拟合的效果。

from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
# 岭回归对波士顿房价进行预测
def ridge():
    # 1. 获取数据集
    boston_data = load_boston()
    # 2. 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston_data.data, boston_data.target, random_state=22)
    # 3. 标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 4. 预估器
    estimator = Ridge()
    estimator.fit(x_train, y_train)
    # 5. 得出模型
    print("权重系数为：", estimator.coef_)
    print("偏置为：", estimator.intercept_)
    # 6. 模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价：", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("岭回归均方误差：", error)

九、分类算法-逻辑回归与二分类

逻辑回归（Logistics Regression）是机器学习中的一种分类模型，虽然名字中带有回归，但逻辑回归是一种分类算法。
应用二分类问题上，要么属于，要么不属于。

• 广告点击率（是否会被点击）
• 是否患病
• 是否为金融诈骗
• 是否为虚假账号

9.1 逻辑回归的原理

逻辑回归的输入就是一个线性回归的结果

• sigmoid函数
  
  回归的结果输入到sigmoid函数当中，输出结果区间在[0, 1]，默认0.5为阈值。

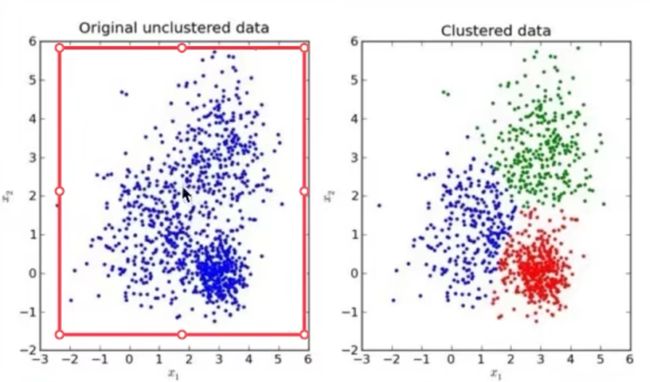
十、无监督学习K-means算法

数据集无特征值，将数据集分类成一簇一簇的。

K-means聚类步骤：

• 随机设置K个特征空间内的点作为初始的聚类中心（K为超参数）
• 对于其他每个点计算到K个中心点的距离，从而选择最近的一个聚类中心作为标记类别
• 聚类中心之后，重新计算出每个聚类的新中心点（平均值）
• 如果计算出来的中心点与原中心点一样，那么结束，否则重新进行第二步过程

10.1 聚类模型评估