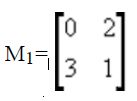DITHER抖动算法
1. 图案法(Patterning)
1.1 什么是图案法?
图案法是指灰度可以用一定比例的黑白点组成的区域表示,从而达到整体图像的灰度感。简单来说,就是使用黑白点组成图案来表示像素的灰度。
1.2 分辨率
在介绍图案法之前,我们先来说一下分辨率。对于不同的对象,分辨率的定义不一样。
对于计算机显示器,打印机,扫描仪等设备来说,分辨率的单位是dpi(dot per inch),即每英寸点数,点数越多,分辨率越高,图像就越清晰。
显示器、打印机、数码相机的分辨率:
- 计算机显示器为15英寸(指对角线长度),最多显示 1280 × 1024 1280×1024 1280×1024个点,显示器的宽高比为 4 : 3 4:3 4:3,所以宽为12英寸,高为9英寸。所以,该显示器的水平分辨率为 ( 1280 / 12 ) d p i (1280/12)dpi (1280/12)dpi,垂直分辨率为 ( 1024 / 9 ) d p i (1024/9)dpi (1024/9)dpi。
- 一般的激光打印机的分辨率是 300 d p i ∗ 300 d p i 300dpi * 300dpi 300dpi∗300dpi, 600 ∗ 600 d p i 600 * 600dpi 600∗600dpi, 720 ∗ 720 d p i 720 * 720dpi 720∗720dpi。
- 一般的设备的分辨率大小:计算机显示器 < 激光打印机 < 扫描仪 < 数码相机。
1.3 图案法介绍
在了解了分辨率之后,我们来做一道计算题。
题目:
假设有一幅 240 ∗ 180 ∗ 8 b i t 240*180*8bit 240∗180∗8bit的灰度图,当使用分辨率为 300 d p i × 300 d p i 300dpi×300dpi 300dpi×300dpi的激光打印机将其打印在 12.8 ∗ 9.6 12.8*9.6 12.8∗9.6英寸的纸上时,每个像素的图案有多大?
答案:
根据分辨率和纸张大小,我们可以得到这张纸最多可以打 ( 300 × 12.8 ) × ( 300 × 9.6 ) = 3840 × 2880 (300×12.8) ×(300×9.6)=3840×2880 (300×12.8)×(300×9.6)=3840×2880个点,所以每个像素可以用 ( 3840 / 240 ) × ( 2880 / 180 ) = 16 × 16 (3840/240)×(2880/180)=16×16 (3840/240)×(2880/180)=16×16个点大小的图案来表示,即一个像素用256个点来表示。如果这 16 × 16 16×16 16×16的方块中一个黑点也没有,就代表灰度256;有一个黑点,就表示灰度255;以此类推,当都是黑点时,表示灰度0。这样, 16 ∗ 16 16*16 16∗16的方块就可以表示257个灰度级,比要求的256个灰度级还多一级。所以,那张图的灰度级可以完全打印出来。
引发疑问:图案如何设计?
上面说到用 16 ∗ 16 16*16 16∗16的图案来表示一个像素,这里就存在一个问题,黑点应该打在哪里?比如说,只有一个黑点时,我们可以打在正中央,也可以打 16 × 16 16×16 16×16的左上角。
图案的设计方法:
图案可以是规则的,也可以是不规则的。一般情况下,有规则的图案比随机图案能够避免点的丛集,但有时会导致图象中有明显的线条。
现在介绍规则图案的设计方法。
如下图所示, 2 × 2 2×2 2×2的图案可以表示5级灰度,不同灰度的图案遵循一定规则:
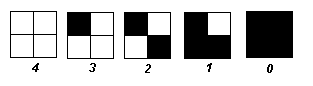
当图像中有一片区域为1的区域时,如下所示,有明显的水平和垂直线条:

再次引发疑问:如何存储庞大的二值点阵?
上面对于5级灰度,需要用5个 2 ∗ 2 2*2 2∗2的矩阵来存储图案,占用的内存就是 5 ∗ 2 ∗ 2 5*2*2 5∗2∗2。
如果想要打印256级灰度的图案,那么就需要存储 256 ∗ 16 ∗ 16 256*16*16 256∗16∗16的二值点阵,这样将占据大量的资源。
存储方法:
有一个更好的方法:只存储一个整数矩阵,称为标准图案,其中的每个值从0到255。图像每个像素的实际灰度和标准图案中的每个值比较,当像素灰度小于等于该值时,图案上的对应点打一黑点。下面举个25级灰度的例子加以说明:
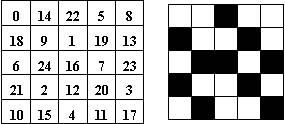
上图,左边为标准图案,右边为灰度为15的像素的图案,共10个黑点,15个白点。要注意的是,5×5的图案可以表示26种灰度,当灰度是25才是全白点,而不是灰度为24时。
下面介绍一种设计标准图案的算法,是由Limb在1969年提出的。笔者就简单的称其为Mn阵了。
1.4 Mn阵(自己起的名字)
-
通过递归关系,有:
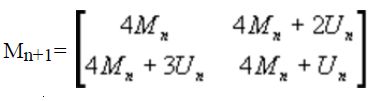
其中Mn和Un均为 2 n × 2 n 2n×2n 2n×2n的方阵,Un的所有元素都是1。根据这个算法,可以得到: -
M3阵
也叫Bayer抖动表,是一个 8 ∗ 8 8*8 8∗8的矩阵,下文还会提到。
总结和提出疑问:根据上面的Mn阵,如果利用M3的话,一个像素需要用 8 ∗ 8 8*8 8∗8的图案表示,则一幅 N ∗ N N*N N∗N的图像将变成 8 N ∗ 8 N 8N*8N 8N∗8N大小。那能不能再保持原图大小的情况下利用图案化技术呢?一种自然的想法是:重新采样,如果使用M3阵,那么就在原图中每 8 ∗ 8 8*8 8∗8的区域采样一个点,然后在应用图案化技术,就能保持原图大小。但这种方法并不行,因为不知道找哪一个点合适,而且 8 ∗ 8 8*8 8∗8的间隔太大了,图案化后会产生严重的失真,如下图所示:

2. 抖动算法
2.1 抖动算法有什么用
上面提到,在应用图案化技术时,如何使图案化后的图像跟原图一样大。然后提到了一种重新采样的方法,但这种方法产生的失真极其严重,所以无法真的使用。
因此,就需要用到抖动算法。其实抖动算法的真正作用不在于设计一种方法来解决图案化技术如何减小存储空间的问题。
先给出抖动算法的作用:
- 以较少的灰度级(颜色),通过抖动来表示更大的灰度级范围(颜色范围)
- 设计一种方案,来使得图案化后的图像不要有太多的失真,尽可能在人的视觉上跟原图差不多。
然后我们来解释一下低灰度级是如何通过抖动来表示更大灰度级范围的。
我们来考虑一下, 即使使用了图案化技术,依然达不到要求的灰度级别。举个例子:假设有一幅 600 × 450 × 8 b i t 600×450×8bit 600×450×8bit的灰度图,当用分辨率为 300 d p i × 300 d p i 300dpi×300dpi 300dpi×300dpi的激光打印机将其打印到 8 × 6 英 寸 8×6英寸 8×6英寸的纸上时,每个象素可以用 ( 2400 / 600 ) × ( 1800 / 450 ) = 4 × 4 (2400/600)×(1800/450)=4×4 (2400/600)×(1800/450)=4×4个点大小的图案来表示,最多能表示17级灰度,无法满足256级灰度的要求。有两种解决方案:(1)减小图象尺寸,由600×450变为150×113;(2)降低图象灰度级,由256级变成16级。这两种方案都不理想。
所以就需要用到抖动技术,看下面。
2.2 Bayer抖动表
原理
假设原图是256灰度级,利用Bayer抖动表,做如下处理:
if (g[y][x]>>2) > bayer[y&7][x&7]
then 打一白点
else 打一黑点
其中,x,y代表原图的象素坐标,g[y][x]代表该点灰度。首先将灰度右移两位,变成64级,然后将x,y做模8运算,找到Bayer表中的对应点,两者做比较,根据上面给出的判据做处理。
实际上,模8运算使得原图分成了一个个8×8的小块,每个小块和8×8的Bayer表相对应。小块中的每个点都参与了比较,这样就避免了上面提到的选点和块划分过大的问题。模8运算实质上是引入了随机成分,但这种随机成分还是有一定规律的。
这种抖动称为规则抖动(regular dithering)。规则抖动的优点是算法简单,缺点是图案化有时很明显,这是因为取模运算虽然引入了随机成分,但还是有规律的。另外,点之间进行比较时,只要比标准图案上点的值大就打白点,这种做法并不理想,因为,如果当标准图案点的灰度值本身就很小,而图象中点的灰度只比它大一点儿时,图象中的点更接近白色,这是视觉效果跟原图就会相差很大。一种更好的方法是将这个误差传播到邻近的象素,就是下面要讲到的Floyd-Steinberg抖动算法。
代码
给出matlab代码实现,用于将256灰度级的图像抖动成同样尺寸的黑白图片。
clear;
clc;
m1 = [[0 2];[3 1]];
u1=ones(2, 2);
m2=[[4*m1 4*m1+2*u1];[4*m1+3*u1 4*m1+u1]]
u2=ones(4, 4);
m3=[[4*m2 4*m2+2*u2];[4*m2+3*u2 4*m2+u2]]
I = imread(‘test.bmp’);
gI = .2989*I(:,:,1)…
+.5870*I(:,:,2)…
+.1140*I(:,:,3);
%imshow(gI);
%r = I(:,:,1);
%g = I(:,:,2);
%b = I(:,:,3);
[h w] = size(gI);
bw = 0;
for i=1:h
for j=1:w
if (gI(i,j) / 4> m3(bitand(i, 7) + 1, bitand(j,7) + 1))
bw(i,j)= 255;
else
bw(i,j)= 0;
end
end
end
imshow(bw);
2.3 Floyd-Steinberg抖动算法
原理
这种算法是误差扩散算法,将当前像素的抖动误差传播到其右侧、下侧、右下侧、左下侧的像素点,其误差传播的模板如下图所示:
给出来以上误差传播模板的抖动算法的伪代码:
for each y from top to bottom
for each x from left to right
oldpixel := pixel[x][y]
newpixel := find_closest_palette_color(oldpixel)
pixel[x][y] := newpixel
quant_error := oldpixel - newpixel
pixel[x + 1][y ] := pixel[x + 1][y ] + quant_error * 7 / 16
pixel[x - 1][y + 1] := pixel[x - 1][y + 1] + quant_error * 3 / 16
pixel[x ][y + 1] := pixel[x ][y + 1] + quant_error * 5 / 16
pixel[x + 1][y + 1] := pixel[x + 1][y + 1] + quant_error * 1 / 16
当然还有其他的误差传播模板,如下图所示:
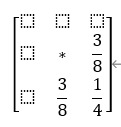
给出来以上误差传播模板的抖动算法的伪代码:
for each y from top to bottom
for each x from left to right
oldpixel := pixel[x][y]
newpixel := find_closest_palette_color(oldpixel)
pixel[x][y] := newpixel
quant_error := oldpixel - newpixel
pixel[x + 1][y ] := pixel[x + 1][y ] + quant_error * 3 / 8
pixel[x ][y + 1] := pixel[x ][y + 1] + quant_error * 3 / 8
pixel[x + 1][y + 1] := pixel[x + 1][y + 1] + quant_error * 1 / 4
注意:上面伪代码中的find_closest_palette_color(oldpixel)其实就是寻找黑点还是白点,比如对于256灰度级来说,当前像素点灰度为120时,因为小于127.5这个阈值,所以当前像素就抖动为0,就是黑点。
举个例子:
假设灰度级别的范围从b(black)到w(white),中间值t为(b+w)/2,对应256级灰度,b=0,w=255,t=127.5。设原图中象素的灰度为g,误差值为e,则新图中对应象素的值用如下的方法得到:
if g > t then
打白点
e=g-w
else
打黑点
e=g-b
3/8 × e 加到右边的象素
3/8 × e 加到下边的象素
1/4 × e 加到右下方的象素
算法的意思很明白:以256级灰度为例,假设一个点的灰度为130,在灰度图中应该是一个灰点。由于一般图象中灰度是连续变化的,相邻象素的灰度值很可能与本象素非常接近,所以该点及周围应该是一片灰色区域。在新图中,130大于128,所以打了白点,但130离真正的白点255还差的比较远,误差e=130-255=-125比较大。将3/8×(-125)加到相邻象素后,使得相邻象素的值接近0而打黑点。下一次,e又变成正的,使得相邻象素的相邻象素打白点,这样一白一黑一白,表现出来刚好就是灰色。如果不传递误差,就是一片白色了。再举个例子,如果一个点的灰度为250,在灰度图中应该是一个白点,该点及周围应该是一片白色区域。在新图中,虽然e=-5也是负的,但其值很小,对相邻象素的影响不大,所以还是能够打出一片白色区域来。这样就验证了算法的正确性。
代码
抖动模板可以设置方向,直接看代码。
clear;
clc;
I = imread(‘0001.jpg’);
img = double(I);%转换图片
[h w] = size(img(:,:,1));%取得图片的大小
d = 1;%为1时,误差从左传递到右侧,为-1时,误差从右传递到左
re = 0;
ge = 0;
be = 0;
rs = 8;%2^n, n = 3 表示将红色量化等级减少到2^5 = 32种。
gs = 8;%2^n, n = 3 表示将绿色量化等级减少到2^5 = 32种。
bs = 8;%2^n, n = 3 表示将蓝色量化等级减少到2^5 = 32种。
for i=1:h
for j=1:w
if (d == 1)
val = rs * fix(img(i,j,1) / rs);
re = img(i, j, 1) - val;
img(i, j, 1) = val;
val = gs * fix(img(i,j,2) / gs);
ge = img(i, j, 2) - val;
img(i, j, 2) = val;
val = bs * fix(img(i,j,3) / bs);
be = img(i, j, 3) - val;
img(i, j, 3) = val;
if ((j + 1) <= w)%计算误差对右侧的像素的传递
img(i, j + 1, 1) = img(i, j + 1, 1) + re * 3 / 8;
img(i, j + 1, 2) = img(i, j + 1, 2) + ge * 3 / 8;
img(i, j + 1, 3) = img(i, j + 1, 3) + be * 3 / 8;
end
if ((i + 1) <= h)%计算误差对下侧的像素传递
img(i + 1, j, 1) = img(i + 1, j, 1) + re * 3 / 8;
img(i + 1, j, 2) = img(i + 1, j, 2) + ge * 3 / 8;
img(i + 1, j, 3) = img(i + 1, j, 3) + be * 3 / 8;
end
if ((i + 1) <= h && (j + 1) <= w)%计算误差对右下侧的像素传递
img(i + 1, j + 1, 1) = img(i + 1, j + 1, 1) + re / 4;
img(i + 1, j + 1, 2) = img(i + 1, j + 1, 2) + ge / 4;
img(i + 1, j + 1, 3) = img(i + 1, j + 1, 3) + be / 4;
end
else
val = rs * fix(img(i,w - j + 1,1) / rs);
re = img(i, w - j + 1, 1) - val;
img(i, w - j + 1, 1) = val;
val = gs * fix(img(i,w - j + 1,2) / gs);
ge = img(i, w - j + 1, 2) - val;
img(i, w - j + 1, 2) = val;
val = bs * fix(img(i,w - j + 1,3) / bs);
be = img(i, w - j + 1, 3) - val;
img(i, w - j + 1, 3) = val;
if ((w - j) > 0)%计算误差对左侧的误差传递
img(i, w - j, 1) = img(i, w - j, 1) + re * 3 / 8;
img(i, w - j, 2) = img(i, w - j, 2) + ge * 3 / 8;
img(i, w - j, 3) = img(i, w - j, 3) + be * 3 / 8;
end
if (i + 1 <= h)%计算误差对下侧的像素误差传递
img(i + 1, j, 1) = img(i + 1, j, 1) + re * 3 / 8;
img(i + 1, j, 2) = img(i + 1, j, 2) + ge * 3 / 8;
img(i + 1, j, 3) = img(i + 1, j, 3) + be * 3 / 8;
end
if ((i + 1) <= h && (w - j) > 0)%计算误差对左下侧的像素误差传递
img(i + 1, w - j, 1) = img(i + 1, w - j, 1) + re / 4;
img(i + 1, w - j, 2) = img(i + 1, w - j, 2) + ge / 4;
img(i + 1, w - j, 3) = img(i + 1, w - j, 3) + be / 4;
end
end
end
d = -d;
end
out = uint8(img);
imshow(out)
close all;
clear all;
clc;
img=imread('pic.bmp');
imshow(img);
[m n]=size(img);
re=zeros(m,n);
tmp=zeros(m+2,n+2);
tmp(2:m+1,2:n+1)=img;
for i=2:m+1
for j=2:n+1
if tmp(i,j)<128
re(i-1,j-1)=0;
err=tmp(i,j);
else
re(i-1,j-1)=255;
err=tmp(i,j)-255;
end
tmp(i,j+1)=tmp(i,j+1)+7/16*err;
tmp(i+1,j-1)=tmp(i+1,j-1)+3/16*err;
tmp(i+1,j)=tmp(i+1,j)+5/16*err;
tmp(i+1,j+1)=tmp(i+1,j+1)+1/16*err;
end
end
figure,imshow(re);
3. 讨论
抖动算法就是用黑白图像来近似灰度图像的一种算法,在结构光中,投影仪存在非线性,导致正弦编码图案实际上在拍摄的图像中并不是正弦性,这样在展开相位就会引入误差,此时就可以用抖动算法将正弦编码图案抖动而二值图案,然后通过投影仪的离焦而得到高质量的正弦图案。