读源码学算法之Octree color quantization

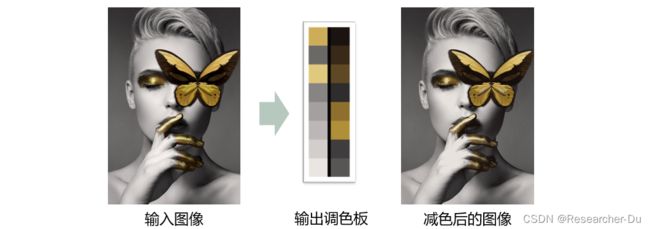
颜色量化（color quantization）技术通过减少颜色数量实现图像的颜色压缩，旨在用尽可能少的颜色去尽可能逼真的还原图片。如下图所示：输入是一张图像，输出是一个调色板（只包含少量的颜色）+ 该调色板还原的输入图像（输入图像中的所有颜色均来自该调色板），最终使得还原后的图像跟输入图像尽可能接近。这种技术最早用于解决低质量设备上显示高质量图像的质量损失问题。

八叉树颜色量化算法于1988年由 M. Gervautz 和 W. Purgathofer 发表：A Simple Method for Color Quantization: Octree Quantization，引用近500次，算法的最大优点是设计巧妙，效率高，占用内存少，选出的调色板最合理，显示效果最好。 下面是一张算法示意图。

论文讲解见：知乎：八叉树颜色压缩图解以及c++实现
我修改了下这篇博客的代码，写了较为详细的注释，故不在进一步解析。

#include 
#define STB_IMAGE_IMPLEMENTATION
#include "stb_image.h"  		//https://github.com/nothings/stb/blob/master/stb_image.h
#define STB_IMAGE_WRITE_IMPLEMENTATION
#include "stb_image_write.h" 	//https://github.com/nothings/stb/blob/master/stb_image_write.h
using namespace std;

int mask[8] = { 128,64,32,16,8,4,2,1 };
int max_color_cnt = 16, color_cnt = 0;

//八叉树节点的数据结构
struct Node{
	bool IsLeaf, Reduceable;
	int count, level, rsum, gsum, bsum, global_pos, childnum;
	Node* pChilds[8];

	Node(int lev) {
		level = lev;
		rsum = gsum = bsum = count = childnum = 0;
		global_pos = -1;
		for (int i = 0; i < 8; i++) pChilds[i] = NULL;
		IsLeaf = false;
		Reduceable = true;
	}
};
vector<Node*> AllTreeNodes; //存放所有节点的数组，每个节点也存了其位置：global_pos
vector<int> LayerNodes[8];  //没放每一层节点的二维数组

//递归的将第idx个节点的所有子孙节点设从树上摘除，(这里实现：将所有后台设定为不可reduce)
void RemoveChildNodesOf(int idx) {
	if (AllTreeNodes[idx]->IsLeaf == true)
		return;

	AllTreeNodes[idx]->Reduceable = false; //不可reduce，因为已经从树上“脱离”
	for (int i = 0; i < 8; i++)
		if (AllTreeNodes[idx]->pChilds[i] != NULL)
			RemoveChildNodesOf(AllTreeNodes[idx]->pChilds[i]->global_pos);
}

void MergeColors(){
	//1.自倒数第二层往树根方向，找到具有最少孩子节点的节点（子节点越少，从该节点分出的颜色越少，越不重要）
	int m_idx = -1;
	for (int i = 7; i >= 0; i--){
		int min_son_cnt = 0x7f7f7f;
		for (int j = 0; j < LayerNodes[i].size(); j++){
			int idx = LayerNodes[i][j];
			if (AllTreeNodes[idx]->Reduceable && AllTreeNodes[idx]->childnum >= 2 && min_son_cnt > AllTreeNodes[idx]->childnum){
				min_son_cnt = AllTreeNodes[idx]->childnum;
				m_idx = idx;
			}
		}
		if (m_idx != -1) break;
	}
	//2.将该节点的孩子从树上摘除，将当前节点设为新的树叶节点，颜色总数更新。
	RemoveChildNodesOf(m_idx);
	AllTreeNodes[m_idx]->IsLeaf = true;
	color_cnt -= (AllTreeNodes[m_idx]->childnum - 1);
}

void AddColor(Node*& pNode, int R, int G, int B, bool newNode){
	if (pNode->level < 8 && newNode)	//将该节点的索引放进所在层中，方便之后搜索
		LayerNodes[pNode->level].push_back(pNode->global_pos);
	if (pNode->IsLeaf) return;			//树叶节点直接返回

	pNode->rsum += R;	//R通道颜色 加到 当前节点的rsum上
	pNode->gsum += G;	//G通道颜色 加到 当前节点的gsum上
	pNode->bsum += B;	//B通道颜色 加到 当前节点的bsum上
	pNode->count += 1;	//该节点颜色总数 + 1

	//非叶子节点
	if (pNode->level < 8) {
		int shift = 7 - pNode->level, Idx = 0;
		//将当前颜色的各通道的第k位合成一个三位的二进制数Idx = (R_kG_kB_k),这也是子节点的位置。
		Idx |= (R & mask[pNode->level]) >> shift << 2;
		Idx |= (G & mask[pNode->level]) >> shift << 1;
		Idx |= (B & mask[pNode->level]) >> shift << 0;

		//如果第Idx节点为空，则创建之，并从新的节点开始继续深入八叉树的下一层。
		if (pNode->pChilds[Idx] == NULL) {
			pNode->pChilds[Idx] = new Node(pNode->level + 1);
			AllTreeNodes.push_back(pNode->pChilds[Idx]);
			pNode->pChilds[Idx]->global_pos = AllTreeNodes.size()-1;
			pNode->childnum += 1;		
			AddColor(pNode->pChilds[Idx], R, G, B, true);
		}
		//如果第Idx节点已经创建，从新的节点开始继续深入八叉树的下一层。
		else
			AddColor(pNode->pChilds[Idx], R, G, B, false);
	}

	//叶子节点，如果颜色总数超过调色板颜色数目，则需要合并某些分支以减少颜色数量。
	else {
		pNode->IsLeaf = true;
		pNode->Reduceable = false;
		if (newNode) {
			color_cnt += 1;
			if (color_cnt > max_color_cnt)
				MergeColors();
		}
	}
}

//颜色量化即替换图像中真实像素颜色，只需要从树根开始，按照添加颜色的方式从上到下遍历，直到叶节点,返回位置。
int QueryColor(Node*& pNode, int R, int G, int B) {
	if (pNode->IsLeaf)
		return pNode->global_pos;

	int shift = 7 - pNode->level, Idx = 0;
	Idx |= (R & mask[pNode->level]) >> shift << 2;
	Idx |= (G & mask[pNode->level]) >> shift << 1;
	Idx |= (B & mask[pNode->level]) >> shift << 0;
	return QueryColor(pNode->pChilds[Idx], R, G, B);
}

int main(){
	int width, height, channels;
	unsigned char* img = stbi_load("bread.png", &width, &height, &channels, 0);

	//1. 先创建八叉树的树根节点
	Node* RootNode = new Node(0);
	AllTreeNodes.push_back(RootNode);
	RootNode->global_pos = 0;
	LayerNodes[0].push_back(0);

	//2. 依次添加输入图像的所有像素颜色
	for (int i = 0; i < height; i++){
		for (int j = 0; j < width; j++){
			int idx = (i * width + j) * channels;
			AddColor(RootNode, img[idx], img[idx + 1], img[idx + 2], false);
		}
	}

	//3.1.图像量化即替换输入图像的颜色，先Query当前颜色，找到八叉树对应的叶子节点.
	//3.2.然后用叶节点的各通道的颜色总和 / 颜色数量 -> 替换之后的颜色。
	for (int i = 0; i < height; i++){
		for (int j = 0; j < width; j++){
			int idx = (i * width + j) * channels;
			int pos = QueryColor(RootNode, img[idx], img[idx + 1], img[idx + 2]);
			img[idx + 0] = AllTreeNodes[pos]->rsum / AllTreeNodes[pos]->count;
			img[idx + 1] = AllTreeNodes[pos]->gsum / AllTreeNodes[pos]->count;
			img[idx + 2] = AllTreeNodes[pos]->bsum / AllTreeNodes[pos]->count;
		}
	}

	stbi_write_png("result.png", width, height, channels, img, width * channels);
	stbi_image_free(img);
}

其它参考：
[1] https://web.cs.wpi.edu/~matt/courses/cs563/talks/color_quant/CQindex.html