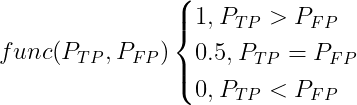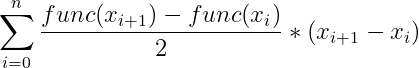混淆矩阵、ROC、AUC 学习记录

        混淆矩阵也称误差矩阵，主要比较分类结果与实际预测值之间的差异可以将分类结果的精度显示在一个混淆矩阵里面。

        下表为二分类问题的混淆矩阵：

	预测为0	预测为1
真实为0	TN	FP
真实为1	FN	TP

        真阴(True Negative)：真实为0，预测也为0；

        假阳(False Positive)：真实为0，预测为1；

        假阴(False Negative)：真实为1，预测为0；

        真阳(True Positive)：真实为1，预测也为1；

        根据以上四种分类，可以得到对于分类模型的不同评价指标：

        准确度(accuray)=(TP+TN) / (TP+FP+FN+TP)；

        精确度(precision)=TP / (TP+FP)；

        召回率(recall)=TP / (TP+FN)；

        以上指标计算原理在理解了混淆矩阵的基础上是显而易见的。

---

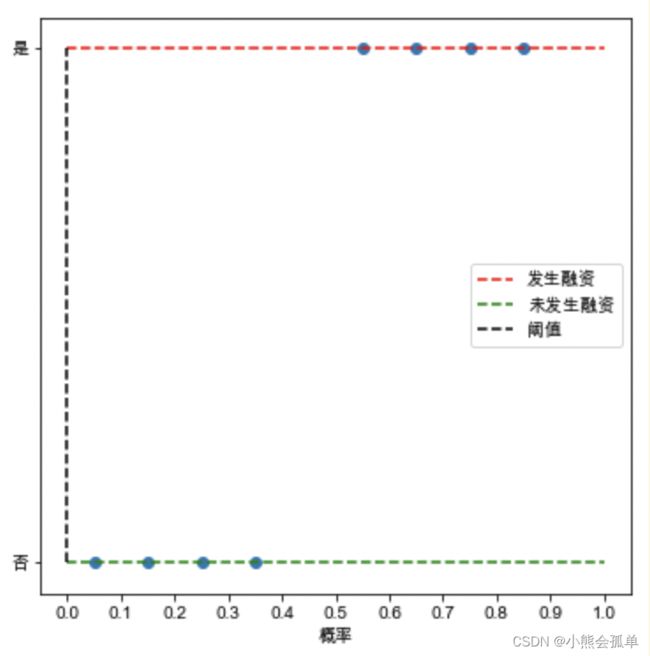
        接下来用一个二分类的例子来引出ROC曲线：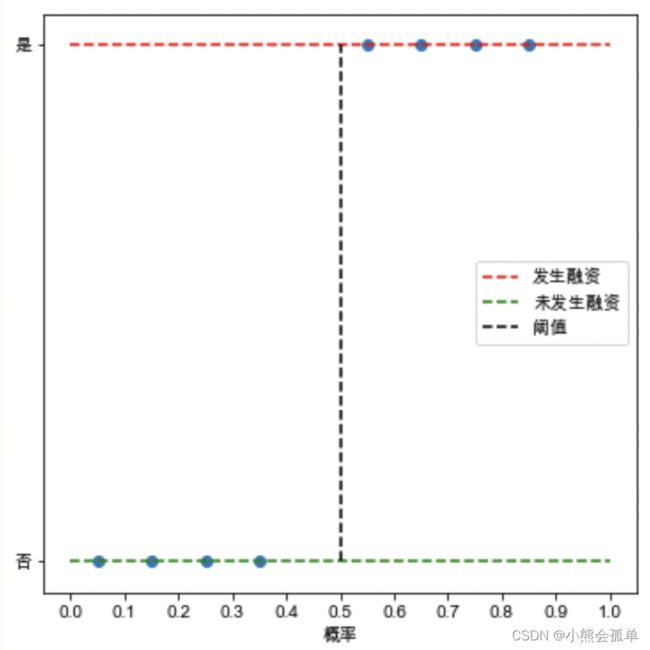
        假设有一分类器被用来通过分类一份公司数据预测该公司是否发生融资，通常分类器将选取一个阈值，如果根据该公司特征分析判断该公司发生融资的概率大于这个阈值，那么分类器将判定该公司将发生融资，反之，则判定不发生融资，左图暂选0.5作为阈值，以图中蓝色圆点代表样本落在红色线上的为实际上会发生融资的样本，落在绿色线上的为实际上不会发生融资的点。可以发现0.5左侧的被判定为未发生融资，0.5右侧的被判定为发生融资，由此可以得到一个混淆矩阵：

阈值0.5	预测未发生	预测发生
实际未发生	4	0
实际发生	0	4

        

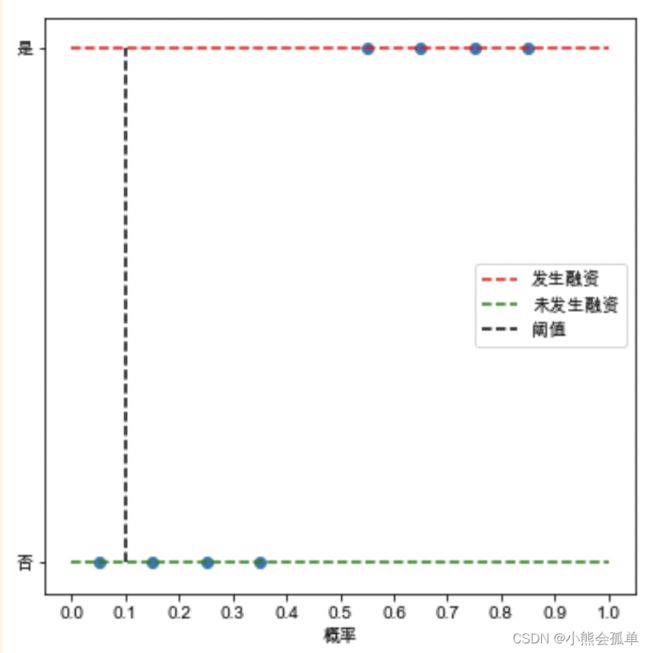
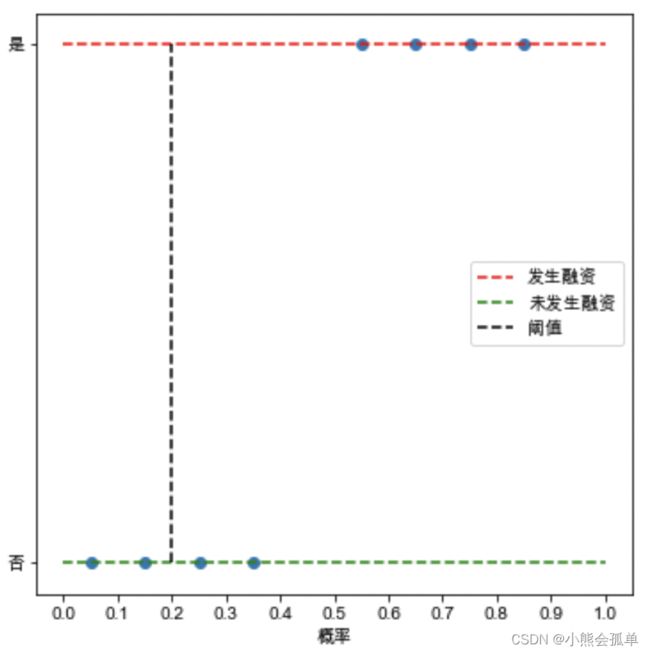
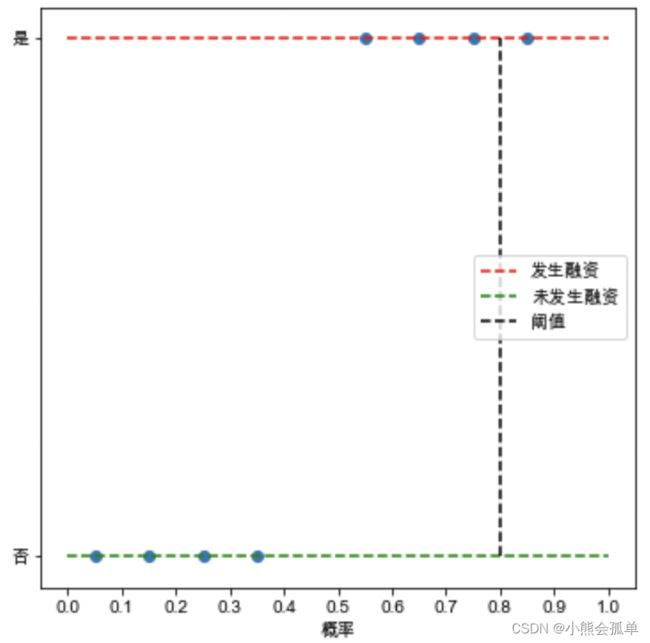
由于阈值选择的不同，可以得到不同的混淆矩阵，从0.0开始依次为：

混淆矩阵依次为：

阈值0.0	预测未发生	预测发生
实际未发生	0	4
实际发生	0	4

阈值0.1	预测未发生	预测发生
实际未发生	1	3
实际发生	0	4

      

阈值0.2	预测未发生	预测发生
实际未发生	2	2
实际发生	0	4

阈值0.8	预测未发生	预测发生
实际未发生	4	0
实际发生	3	1

---

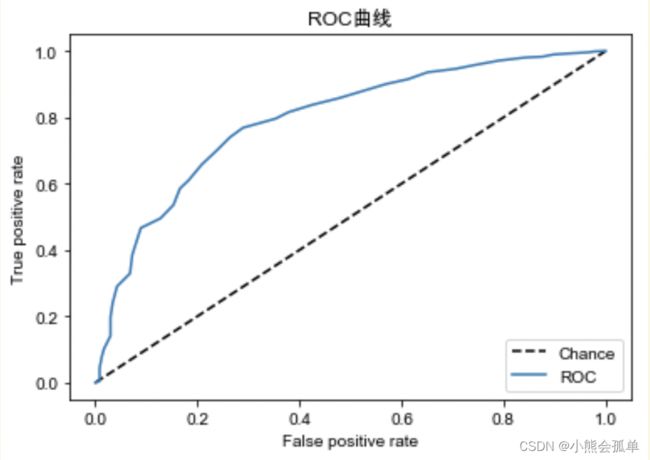
        若阈值选取更加细化，就意味着有更多的混淆矩阵，为了能直观的表现这些混淆矩阵，引入了ROC曲线，ROC曲线实际上就是不同阈值选择下的混淆矩阵映射到一个二维空间的点所连成的一条曲线，以这次学习的模型训练结果画出的ROC曲线为例：

         ROC曲线的横坐标为 假阳率(False positive rate)，纵坐标为真阳率(True positive rate)，基于对混淆矩阵的理解，我们几乎总是希望模型测试结果的真阳率尽可能高的同时，假阳率尽可能的低，把这种混淆矩阵映射到上面的二维空间时，它的坐标一定是更靠近左上的，而ROC曲线的实质就是多个不同阈值下的矩阵在二维空间中的连线，所以我们可以得到ROC曲线越靠近左上角，模型表现越优秀的结论。

        但“ROC曲线更靠近左上角”这样的说法显然不具备标准性，我们更习惯于用一个确切的指标来帮助衡量模型的表现，观察发现ROC曲线更靠近左上角”可以转换为ROC曲线下方面积的大小判断，即下方面积越大，模型表现越优秀，反之越糟糕。由此引出了AUC(ROC曲线下方面积的值)这个指标(注：理论上AUC值的取值范围在0～1之间，实际上在0.5～1之间，当AUC=0.5时，模型表现与抛硬币无异，AUC低于0.5时模型预测起反效果还不如乱猜，此时可以取模型预测结果的对立面作为最终结果)。下面给出AUC的计算方法，与python代码实现。并对比Sklearn中内置的计算AUC方法验证结果正确性：

法一： 

        在有M个标签为阳的样本，N个标签为阴的样本中，一共有M*N对样本(一个阴，一个阳)，计算这M*N对样本中阳样本被预测为阳的概率大于阴样本被预测为阳的概率的概率。也就是真阳率大于假阳率的概率。

        公式为：

                  

     

python代码如下：

#获取阳性概率估计
pre=clf.predict_proba(X_test)[:,1]
#定义一个变量auc用来保存计算auc的结果
auc=0
#取出阳样本标签和阴样本标签索引
pos=[i for i in range(len(y_test)) if y_test[i]==1]
neg=[i for i in range(len(y_test)) if y_test[i]==0]
#配对比较概率
for i in pos:
    for j in neg:
        if pre[i]>pre[j]:
            auc+=1
        elif pre[i]==pre[j]:
            auc+=0.5
auc=auc/(len(pos)*len(neg))
auc

对比sklearn中计算AUC的算法：

from sklearn.metrics import roc_auc_score
roc_auc_score(y_true=y_test,y_score=pre)

 

       法二：

       根据sklearn.metrics.roc_curve所返回的FPR,TPR都是有序的，我们可以利用微积分思想划分小区间进行近似计算(将原有的面积划分为n份)：

                ​​​​​​​        ​​​​​​​        

                     ​​​​​​​        ​​​​​ ​​​​​​​  为第i个小区间右边届的y值，为第i个小区间左边届的y值上述公式取他们的平均值再与小区间长度相乘，依次对所有的小区间求和最终得到AUC的近似值。

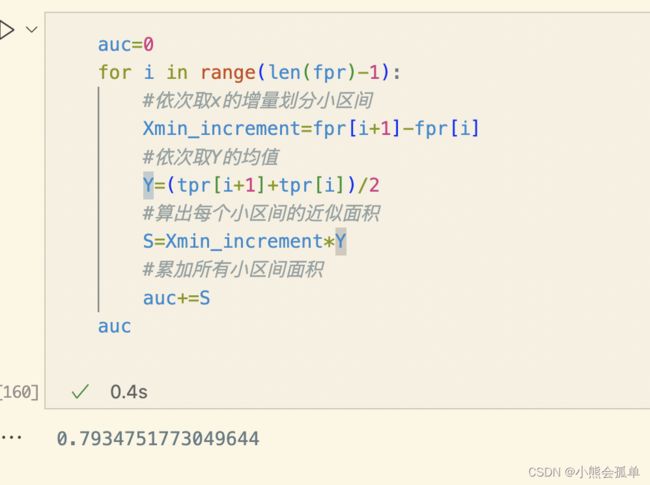
auc=0
for i in range(len(fpr)-1):
    #依次取x的增量划分小区间
    Xmin_increment=fpr[i+1]-fpr[i]
    #依次取Y的均值
    Y=(tpr[i+1]+tpr[i])/2
    #算出每个小区间的近似面积
    S=Xmin_increment*Y
    #累加所有小区间面积
    auc+=S
auc

 可以看到这个差异值可以忽略不计了。如果样本数量再多一些的话，划分将更加细致精确度也会更高。