社区发现(三)：LPA算法（标签传播算法）

引用：https://blog.csdn.net/itplus/article/details/9286905
引用：https://www.jianshu.com/p/0c66b2717972

LPA（Label Propagation Algorithm）由Usha Nandini Raghavan等人于2007年提出。

1. 基本思想

标签传播算法（LPA）是基于图的半监督学习算法，基本思路是从已标记的节点标签信息来预测未标记的节点标签信息，利用样本间的关系，建立完全图模型，适用于无向图。
每个节点标签按相似度传播给相邻节点，在节点传播的每一步，每个节点根据相邻节点的标签来更新自己的标签，与该节点相似度越大，其相邻节点对其标注的影响权值越大，相似节点的标签越趋于一致，其标签就越容易传播。在标签传播过程中，保持已标记的数据的标签不变，使其将标签传给未标注的数据。最终当迭代结束时，相似节点的概率分布趋于相似，可以划分到一类中。

2. 算法描述

（1）算法符号介绍
$(x_1,y_1),...,(x_l,y_l)$：已标注的数据

$Y_L=\{y_1,...,y_L\}\in \{1,...,C\}$：已标注数据的类别。$C$已知，且存在于标签数据中

$(x_{l+1},y_{l+1}),...,(x_{l+u},y_{l+u})$：未标注数据

$Y_U=\{y_{l+1},...,y_{l+u}\}$：没有标签，满足$L<<u$，即有标签的数据数量远小于没有标签的数据数量

$X=\{x_1,...,x_{l+u}\}\in R^D$

问题：从$X$和$Y_L$去预测$Y_U$

（2）全连接图建立
相邻的数据点具有相同的标签，建立一个全连接图，让每一个样本点(有标签的和无标签的)都作为一个节点。用以下权重计算方式来设定两点i, j之间边的权重，所以两点间的距离$d_{ij}$越小，权重$w_{ij}$越大。
$$w_{ij}=exp(-\frac{d_{ij}}{{\sigma }^2})=exp(-\frac{{\sum }_{d=1}^D(x_i^d-x_j^d)}{{\sigma }^2})$$
然后让每一个带有标签的节点通过边传播到所有的节点，权重大的边的节点更容易影响到相邻的节点。

（3）定义概率传播矩阵
$T\in (l+u)\times (l+u)$，元素$T_{ij}$为标签j传播到标签i的概率。
$$T_{ij}=P(j\to i)=\frac{w_{ij}}{{\sum }_{k=1}^{l+u}{w}_{kj}}$$
（4) 定义标签矩阵（也称soft label矩阵）
$Y\in (l+u)\times C,Y_{i,C}=\delta (y_i,C)$，第i行表示节点$y_i$的标注概率。$Y_{i,C}=1$说明节点$y_i$的标签为C。通过概率传播，使其概率分布集中于给定类别，然后通过边的权重来传递节点标签。

3. 算法流程

输入： $l$个标记的数据及标签，$u$个未标记数据；

输出：$u$个未标记数据的标签

第1步：初始化，利用权重公式计算每条边的权重$w_{ij}$，得到数据间相似度；

第2步：根据得到的权重$w_{ij}$，计算节点$j$到节点$i$的传播概率$T_{ij}$；

第3步：定义矩阵$Y\in (l+u)\times C$;

第4步：执行传播，每个节点按传播概率将周围节点传播的标注值按权重相加，并更新到自己的概率分布，$Y^t=T\times Y^{t-1}$。

第5步：重置$Y$中已标记样本的标签，限定已标注的数据，把已标注的数据的概率分布重新赋值为初始值；

第6步：重复步骤4和5，直至$Y$收敛。

步骤5非常关键，因为已标记数据是事先确定的，不能被带跑，每次传播完都得回归本来的标签。

4. 标签传播算法的变形

每次迭代都要计算标签矩阵$Y$，但是$Y_L$是已知的，计算用处不大。在步骤5中，还需重设初始值。可以将矩阵$T$做以下划分：
$$T=\left[\begin{array}{cc}{T}_{LL}& T_{LU}\\ T_{UL}& T_{UU}\end{array}\right]$$
只需更新运算：
$$Y_U\leftarrow T_{UU}{Y}_U+P_{UL}{Y}_L$$
迭代至收敛。

5. LPA算法的python实现

实现方式：scikit-learn示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.semi_supervised import label_propagation
from sklearn.datasets import make_circles

# generate ring with inner box
n_samples = 200
X, y = make_circles(n_samples=n_samples, shuffle=False)
outer, inner = 0, 1
labels = np.full(n_samples, -1.)
labels[0] = outer
labels[-1] = inner
# Learn with LabelSpreading
label_spread = label_propagation.LabelSpreading(kernel='rbf', alpha=0.8)
label_spread.fit(X, labels)

# Plot output labels
output_labels = label_spread.transduction_
plt.figure(figsize=(8.5, 4))
plt.subplot(1, 2, 1)
plt.scatter(X[labels == outer, 0], X[labels == outer, 1], color='navy',
            marker='s', lw=0, label="outer labeled", s=10)
plt.scatter(X[labels == inner, 0], X[labels == inner, 1], color='c',
            marker='s', lw=0, label='inner labeled', s=10)
plt.scatter(X[labels == -1, 0], X[labels == -1, 1], color='darkorange',
            marker='.', label='unlabeled')
plt.legend(scatterpoints=1, shadow=False, loc='upper right')
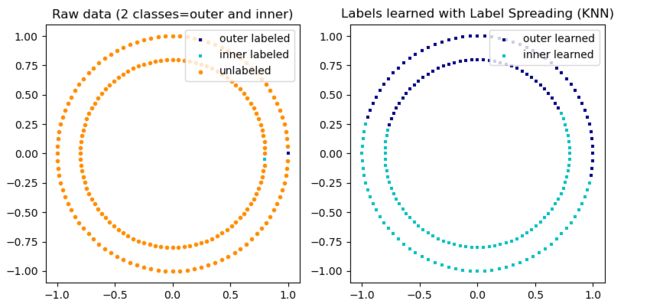
plt.title("Raw data (2 classes=outer and inner)")

plt.subplot(1, 2, 2)
output_label_array = np.asarray(output_labels)
outer_numbers = np.where(output_label_array == outer)[0]
inner_numbers = np.where(output_label_array == inner)[0]
plt.scatter(X[outer_numbers, 0], X[outer_numbers, 1], color='navy',
            marker='s', lw=0, s=10, label="outer learned")
plt.scatter(X[inner_numbers, 0], X[inner_numbers, 1], color='c',
            marker='s', lw=0, s=10, label="inner learned")
plt.legend(scatterpoints=1, shadow=False, loc='upper right')
plt.title("Labels learned with Label Spreading (KNN)")

plt.subplots_adjust(left=0.07, bottom=0.07, right=0.93, top=0.92)
plt.show()

结果展示：