python计算线性代数(矩阵的相关计算)
更多文章:
python计算微积分:http://t.csdn.cn/6g5DH
python求解方程的根:http://t.csdn.cn/3MtoP
python查看圆周率π的后10000位:http://t.csdn.cn/84Uwt
R语言矩阵的相关计算:http://t.csdn.cn/ya8vS
本文介绍如何用sympy库计算线性代数
同样是使用python的sympy库,安装方法有很多这里就不介绍了
一.矩阵的创建
创建以下矩阵:
$$
$$
( 2 1 ) \left( \begin{array}{c} 2\\ 1\\ \end{array} \right) \,\, (21)
from sympy import *
Matrix([1,2])
如果输出为空,请print(Matrix([1,2])),以下同理
( 2 , 1 ) \left( 2,1 \right) (2,1)
from sympy import *
Matrix([[2,1]])
( 1 2 3 4 ) \left( \begin{matrix} 1& 2\\ 3& 4\\ \end{matrix} \right) (1324)
from sympy import *
Matrix([[1,2],[3,4]])
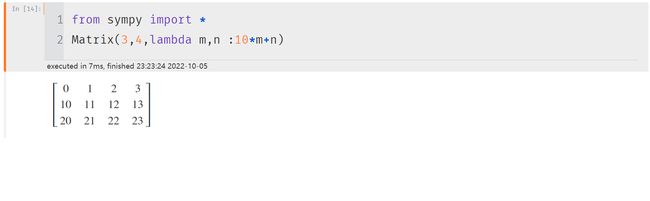
( 0 1 2 3 10 11 12 13 20 21 22 23 ) \left( \begin{matrix} 0& 1& 2& 3\\ 10& 11& 12& 13\\ 20& 21& 22& 23\\ \end{matrix} \right) ⎝ ⎛01020111212122231323⎠ ⎞
不难发现第2行等于10+对应第一行的数字,第3行等于20+对应第一行的数字,第一行也很有规律,我们可以使用lambda函数
( a b c d ) \left( \begin{matrix} a& b\\ c& d\\ \end{matrix} \right) (acbd)
因为这里的a,b,c,d都是变量,所以我们应该先定义他:
from sympy import *
a,b,c,d=symbols("a,b,c,d")
Matrix([[a,b],[c,d]])
二.矩阵的相关计算
| 函数/方法 | 说明 |
|---|---|
| 矩阵乘法 | *(就直接乘) |
| transpose/T | 计算矩阵的转置矩阵 |
| adjoint/H | 计算矩阵的伴随矩阵 |
| trace | 计算矩阵的迹(主对角元素之和) |
| det | 计算矩阵的行列式 |
| inv | 计算矩阵的逆矩阵 |
| LUsolve | 使用LU分解计算形如Mx=b的线性方程组 |
| Qsolve | 使用QR分解计算形如Mx=b的线性方程组 |
| solve | 计算形如Mx=b的线性方程组 |
1.矩阵乘法
A = ( a b c d ) , B = ( 1 2 3 4 ) , 计算 A B A=\left( \begin{matrix} a& b\\ c& d\\ \end{matrix} \right) ,B=\left( \begin{matrix} 1& 2\\ 3& 4\\ \end{matrix} \right) ,\text{计算}AB A=(acbd),B=(1324),计算AB
from sympy import *
a,b,c,d=symbols("a,b,c,d")
A=Matrix([[a,b],[c,d]])
B=Matrix([[1,2],[3,4]])
A*B
2.求逆矩阵
计算 B = ( 1 2 3 4 ) 的逆矩阵 \text{计算}B=\left( \begin{matrix} 1& 2\\ 3& 4\\ \end{matrix} \right) \text{的逆矩阵} 计算B=(1324)的逆矩阵
from sympy import *
B=Matrix([[1,2],[3,4]])
B.inv()
3.计算B转置
from sympy import *
B=Matrix([[1,2],[3,4]])
B.transpose()
#或者
B.T#没有括号
4.计算B的行列式
from sympy import *
B=Matrix([[1,2],[3,4]])
det(B)
-2
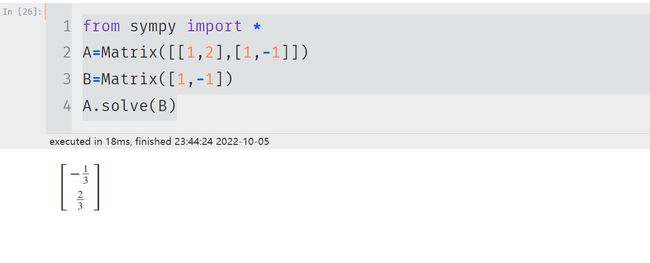
5.计算线性方程组
{ x + 2 y − 1 = 0 x − 2 y + 1 = 0 \begin{cases} x+2y-1=0\\ x-2y+1=0\\ \end{cases} {x+2y−1=0x−2y+1=0
首先我们要先移项,在分别创建系数矩阵和常数矩阵
{ x + 2 y = 1 x − 2 y = − 1 \begin{cases} x+2y=1\\ x-2y=-1\\ \end{cases} {x+2y=1x−2y=−1
from sympy import *
A=Matrix([[1,2],[1,-1]])
B=Matrix([1,-1])
A.solve(B)
6.计算B的伴随矩阵(为什么计算错误)
很明显这里出现了错误,我也不知道为什么
from sympy import *
B=Matrix([[1,2],[3,4]])
B.adjoint()
参考文章:python科学计算和数据科学应用