排序算法总结笔记
文章目录
-
- 冒泡排序
- 插入排序
- 希尔排序
- 选择排序
- 堆排序
- 快速排序递归法
- 优化方法,三数取中
- hoare版本
- 挖坑法
- 前后指针法
-
- 非递归快排
- 归并排序递归法
- 非递归的归并排序
- 计数排序
冒泡排序
冒泡排序思想简述:
假设有10个元素,其实要跑9躺,每一趟的目的就是把最大的值放到最后一个位置(假设需要升序)
第1躺,只用比较9对元素
2 8
3 7
…
9 1
void BubbleSort(int* a, int sz)
{
int i = 0;
for (i = 0; i < sz - 1; i++) //控制躺数
{
int flag = 0;
int j = 0;
for (j = 0; j < sz - 1 - i; j++) //控制比较对数
{
if (a[j] < a[j + 1])
{
flag = 1;
Swap(&a[j], &a[j + 1]);
}
}
if (flag == 0) //如果一堂跑下来没有元素交换,那么就已经有序,就不需要在进行下一躺
{
break;
}
}
}
插入排序
在下标end的位置后面取一个数,如果比这个数大,end向后覆盖,end–,然后再比较,如果小于,break
这时候要做end+1的位置把那个保存的值tmp放进去。
void InsertSort(int* a, int sz)
{
int i = 0;
for (i = 0; i < sz - 1; i++) //控制下标
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end]; //如果tmp小于end位置,end位置就要向后覆盖
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
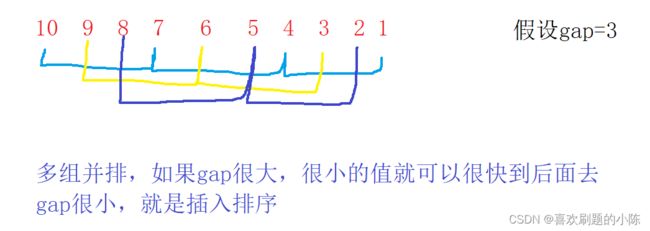
希尔排序
void ShellSort(int* a, int sz)
{
int gap = sz;
while (gap > 1)
{
//gap==1,直接插入排序,如果代码不好想,完全可以把
//把直接插入排序的-1想成gap
gap = gap / 3 + 1;
int i = 0;
for (i = 0; i < sz - gap; i++) //i++控制多组并排,控制下标最大sz-1,防止下面的end+gap越界
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
选择排序
//找最小,放到最左边,找最大,放到最右边,然后更新最左边和最右边
void SelectSort(int* a, int sz)
{
int left = 0;
int right = sz - 1;
while (left < right)
{
int i = 0;
int mini = left, maxi = left;
for (i = left+1; i <= right; i++)
{
//找小
if (a[i] > a[mini])
{
mini = i;
}
//找大
if (a[i] < a[maxi])
{
maxi = i;
}
}
//left和right肯定不会重叠,maxi和mini也不会,right和mini重叠也没关系
//如果最左边就是最大值,left和maxi重叠,这里就需要更新一下maxi
Swap(&a[left],&a[mini]);
if (left == maxi)
{
maxi = mini;
}
Swap(&a[right], &a[maxi]);
left++;
right--;
}
}
堆排序
void AdjustDown(int* a, int sz, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child < sz)
{
if (child + 1 < sz && a[child + 1] > a[child])
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int sz)
{
//对数组建堆 ,建大堆,升序;建小堆,降序
int i = 0;
for (i = (sz - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, sz, i);
}
//每次取堆顶元素,与最后一个交换,再从堆顶向下调整
int end = sz - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
快速排序递归法
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if (end - begin >= 10) //小区间优化法
{
InsertSort(a + begin, end-begin+1); //小区间优化法,都是闭区间,而插入排序的参数是数组
} //元素的个数
int key = PartSort1(a, begin, end);
//像二叉树一样层层递归下去(分治法)
QuickSort(a, begin, key - 1);
QuickSort(a, key+1, end);
}
优化方法,三数取中
int GetMidIndex(int* a, int left, int right)
{
int mid = ((right - left) >> 1) + left;
if (a[left] < a[right])
{
if (a[mid] < a[left])
return mid;
else if (a[right] < a[mid])
return right;
else
return left;
}
else //a[left] > a[right]
{
if (a[mid] < a[right])
return right;
else if (a[left] < a[mid])
return left;
else
return mid;
}
}
hoare版本
//hoare版本
int PartSort1(int* a, int left, int right)
{
//三数取中
int mid = GetMidIndex(a, left, right);
Swap(&a[mid], &a[left]);
int keyi = left;
//key在左边,right先走,可保证在小于key的位置停下
//第1种情况,left碰right,right肯定已经在小于的位置停下
//第2种情况,right碰left,right肯定是找小才向左走,不然肯定会在大的位置停下
while (left < right)
{
while (left < right && a[right] >= a[keyi])
right--;
while (left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left; //left == right 停下,返回谁都ok呀
}
挖坑法
//挖坑法
int PartSort2(int* a, int left, int right)
{
//三数取中
int mid = GetMidIndex(a, left, right);
Swap(&a[mid], &a[left]);
int pit = left; //坑在left,right先走
int key = a[left]; //保存下坑的值
while (left < right)
{
while (left < right && a[right] >= key)
right--;
a[pit] = a[right];
pit = right; //更新一下坑位
while (left < right && a[left] <= key)
left++;
a[pit] = a[left];
pit = left;
}
a[pit] = key;
return pit;// left和right最终会在坑位遇见
}
前后指针法
//前后指针法 key在左
int PartSort3(int* a, int left, int right)
{
//三数取中
int mid = GetMidIndex(a, left, right);
Swap(&a[mid], &a[left]);
int keyi = left, pre = left, cur = left+1;
while (cur <= right)
{
//pre会一直在小的位置,pre+1就是大的位置
//cur找小,找到pre++,等于就是同一个位置
//因为cur一直会在前,如果cur在大的位置,cur自己走,pre就会停在大的位置前面,也就是小
//如果cur遇到小,那么++pre肯定是在大的位置
if (a[cur] <= a[keyi] && a[++pre] != a[cur])
Swap(&a[cur], &a[pre]);
cur++;
}
Swap(&a[left], &a[pre]);
return pre;
}
//前后指针法,key在右边
int PartSort4(int* a, int left, int right)
{
//三数取中
int mid = GetMidIndex(a, left, right);
Swap(&a[mid], &a[right]);
int keyi = right, pre = left-1, cur = left;
while (cur < right)
{
if (a[cur] <= a[keyi] && a[++pre] != a[cur])
Swap(&a[cur], &a[pre]);
cur++;
}
Swap(&a[++pre], &a[keyi]); //为什么要++pre? 因为pre一定停在了小的位置,
return pre; //而我们要将大的位置换到后面去
}
非递归快排
//使用栈 ,先全部一下,然后右边排完再排右边
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
StackInit(&st);
StackPush(&st, begin);
StackPush(&st, end);
while (!StackEmpty(&st))
{
int right = StackTop(&st); //这里左,右区间要注意一下,先入后出的性质
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
int key = PartSort1(a, left, right);
//left,key-1 key+1,right
if (left < key - 1)
{
StackPush(&st, left);
StackPush(&st, key - 1);
}
if (key + 1 < right)
{
StackPush(&st, key + 1);
StackPush(&st, right);
}
}
StackDestory(&st);
}
//使用队列的方式---左边排一下,右边排一下(左右并排)
void QucikSortNonRQueue(int* a, int begin, int end) //使用队列
{
Queue q;
QueueInit(&q);
QueuePush(&q, begin);
QueuePush(&q, end);
while (!QueueEmpty(&q))
{
int left = QueueFront(&q);
QueuePop(&q);
int right = QueueFront(&q);
QueuePop(&q);
int key = PartSort1(a, left, right);
//left, key-1 key+1,right
if (left < key - 1)
{
QueuePush(&q, left);
QueuePush(&q, key-1);
}
if (key + 1 < right)
{
QueuePush(&q, key + 1);
QueuePush(&q, right);
}
}
QueueDestroy(&q);
}
归并排序递归法
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end) //一个元素不需要归并
return;
int mid = begin + (end - begin) / 2;
_MergeSort(a, begin, mid,tmp);
_MergeSort(a, mid + 1, end,tmp);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int index = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[index++] = a[begin1++];
else
tmp[index++] = a[begin2++];
}
while (begin1 <= end1)
tmp[index++] = a[begin1++];
while (begin2 <= end2)
tmp[index++] = a[begin2++];
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int sz)
{
int* tmp = (int*)malloc(sizeof(int) * sz);
_MergeSort(a, 0, sz - 1, tmp);
}
非递归的归并排序
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += gap * 2) // 2组元素归并,跳过两组元素
{
int left1 = i, right1 = i + gap - 1;
int left2 = i + gap, right2 = i + 2 * gap - 1;
int index = i;
//防止越界,调整一下
if (right1 >= n)
right1 = n - 1;
if (left2 >= n)
{
left2 = n;
right2 = n - 1;
}
if (right2 >= n)
right2 = n - 1;
while (left1 <= right1 && left2 <= right2) //两个区间有一个归并完才可以
{
if (a[left1] < a[left2])
tmp[index++] = a[left1++];
else
tmp[index++] = a[left2++];
}
while (left1 <= right1)
tmp[index++] = a[left1++];
while (left2 <= right2)
tmp[index++] = a[left2++];
}
gap *= 2;
memcpy(a, tmp, sizeof(int) * n);
}
free(tmp);
tmp = NULL;
}
计数排序
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
int range = max - min + 1; //范围(元素个数)
int* CountArray = (int*)calloc(range,4);
assert(CountArray);
for (int i = 0; i < n; i++)
{
CountArray[a[i] - min]++;
}
int k = 0;
for (int j = 0; j < range; j++)
{
while (CountArray[j])
{
a[k++] = j + min;
CountArray[j]--;
}
}
}