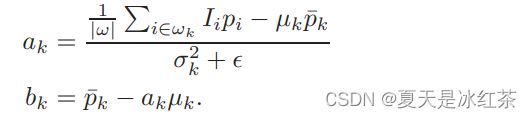图像处理：推导五种滤波算法（均值、中值、高斯、双边、引导）

目录

概论

算法原理

1、均值滤波

2、中值滤波

3、高斯滤波

4、双边滤波

5、引导滤波

 手写代码

Opencv代码实现

 最后的总结

参考文章

---

概论

        本来打算是分开推导的，但我觉得还是整个合集吧，避免有水文的嫌疑，那么因为学习的需要，会涉及到图像的滤波处理，我汇总了一些常见的滤波算法，方便日后查看。

---

算法原理

1、均值滤波

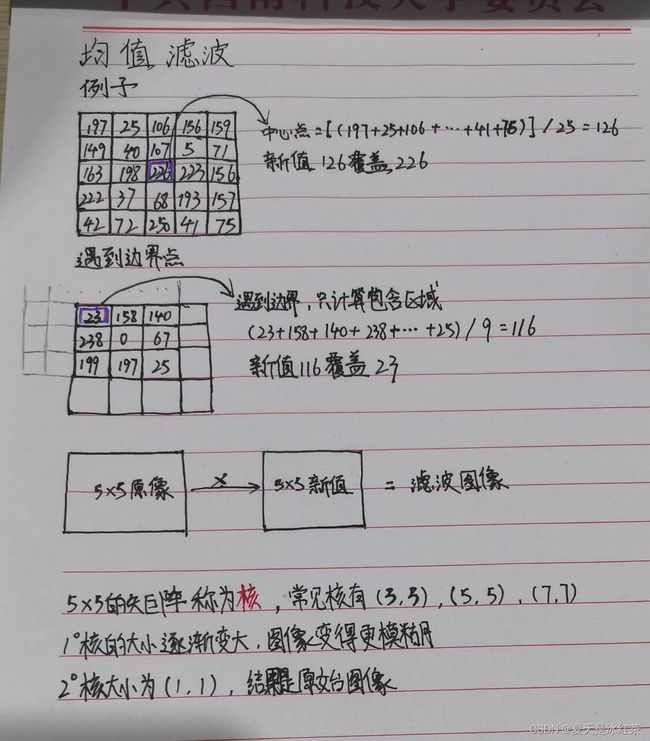
        我将以5*5的区域为例子来讲解：

此时，中心点就很容易的被确定了，将所有的数全部加起来后，求取平均值取代中心点的中间值，但是图像的边界并不存在5*5的区域，那么只需要提取在图像内的周围点的像素平均值。

附带草稿图：

均值滤波本身会存在缺陷，即他不能很好的保护好图像的细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，尤其是在处理椒盐滤波的时候。 

2、中值滤波

        其与中值滤波相似，同样是选定固定的大小核，选取其中所有像素值的中位数作为滤波结果，类似的就是在比赛当中，去掉最高分和最低分，其余分数求取平均值，这个就叫做中位值平均滤波法，但这种方法就效率而言有点慢了。

附带草稿图：

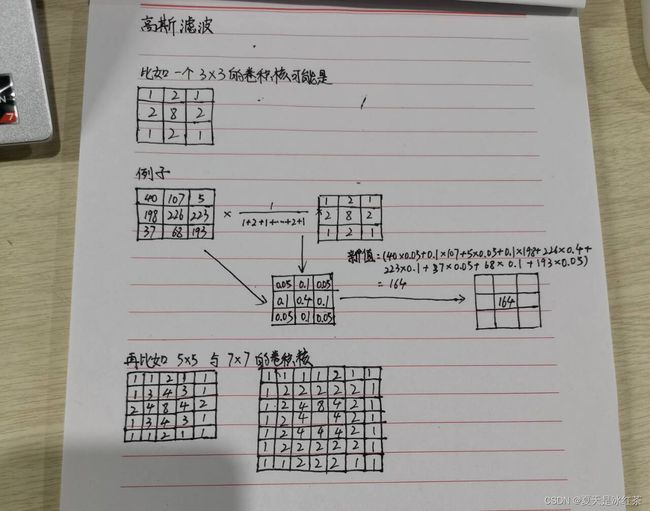
3、高斯滤波

使用一个模板，常常称为卷积或掩膜，来扫描图像中的每一个像素，用模板确定的领域内的像素的加权平均值去替代模板中心像素点的值。

附带草稿：

在高斯滤波当中，核的宽度和高度可以不相同，但都要是奇数。

同一尺寸的卷积核都可以有多种不同的形式，比如在下面的图中5*5：

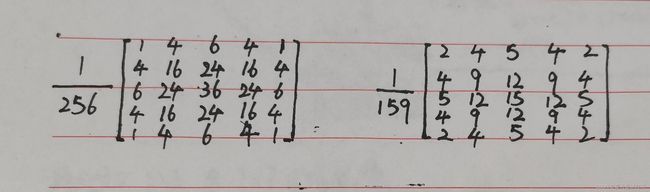
同一尺寸的卷积核可以有不同的权重比，在实际的计算当中，卷积核是归一化处理的，这种处理方式可以参考上面的3*3的卷积核（都是小数的），但有的资料当中并没有进行归一化，这时就可能是如我上图当中举出来的5*5，7*7的卷积核，这样的卷积核是为了说明问题用的，实际在用的时候还是需要进行归一化，准确来说，没有经过归一化的卷积核得到的结果往往是错误的。

4、双边滤波

双边滤波是一种不同于以往的平滑滤波，是一种常用于像素边缘保持的空间非线性滤波方法，主要利用了领域内像素点的空间邻近度和像素值相似度来构建高斯权重滤波器。

附带草稿图：

 图2：

5、引导滤波

引导滤波为何凯明等人于2010年提出，它本质上具有O(N)复杂度，相当于双边滤波有更好的边缘保持特性，且不会出现梯度反转的现象，在不同引导图像的引导下，可广泛应用于降噪、去雾、高动态范围压缩等。在其定义当中，用到了局部线性模型，该模型认为，某函数上一点与其邻近部分的点成线性关系，一个复杂的函数就可以用很多局部的线性函数来表示，当需要求该函数上某一点的值时，只需计算所有包含该点的线性函数的值并作平均即可。

以下皆为对此的翻译以及个人解释：

GuidedFilter.dvi (kaiminghe.com)http://kaiminghe.com/publications/eccv10guidedfilter.pdf对于一个输入图像p，通过引导图像I，经过滤波后得到输出图像q，其中p和I都是算法的输入。引导滤波定义了如下所示的一个线性滤波过程，对于i位置的像素点，得到的滤波输出是一个加权平均值：

                                   

 其中i和j分别表示像素的下标。Wij是只和引导图像I相关的滤波核。该滤波器相对于p是线性的，双边滤波核Wbf由下式给出：

                         
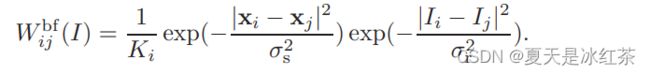
其中x是像素坐标，Ki是规格化参数，以确保Wij的和为1，参数σs和σr调整空间相似性和范围（强度/颜色）相似性。联合双边滤波器退化当I和p相同时，初始双边滤波器。

现在我们定义导向滤波器及其内核。被引导者的关键假设滤波器是制导I和滤波器输出q之间的局部线性模型。我们假设q是以像素k为中心的窗口ωk中I的线性变换：

                              

 I

其中（ak，bk）是假定在ωk中为常数的一些线性系数。我们使用半径为r的方形窗口。这种局部线性模型确保q有一条边除非我有优势，因为∇q=a∇I、 该模型已被证明在图像消光、图像超分辨率和烟雾消除。为了确定线性系数，我们寻求上面式子的一个最小化的解q和滤波器输入p之间的差值。具体来说，我们将窗口中的以下成本函数：

                        

 这里是一个正则化参数，用于防止ak过大。上面的解可以通过线性回归得出：

                            

 这里，μ（k）和σ（k）**2是I在ωk中的平均值和方差，|ω|是ωk中的像素数，¯pk是ωk中p的平均值。通过此修改∇q不再是的缩放∇一、 因为线性系数（¯ai，¯bi）在空间上变化。但由于（¯ai，¯bi）是平均滤波器的输出，它们的梯度应该比强边附近的I小得多。在这种情况下，我们仍然可以∇q≈ a¯∇I、 这意味着I中的突然强度变化大部分可以在q中保持。

 核重量可以明确表示为：

                     

 

进一步的计算表明和的Wij（I）=1。不需要额外努力以规范化权重。

对于该算法，当I = p I=pI=p时，即输入图像和引导图像是同一副图像时，该算法即成为一个边缘保持滤波器。同时，方程的解也可作如下表示：    
                             

                                

 手写代码

本文只以手写的中值滤波来实现，其他的方法滤波器大家可以自己去尝试以下：

import numpy as np
import cv2

def medianBlur(image, ksize=2):

    rows, cols = image.shape[:2]
    half = ksize // 2
    start = half
    end = rows-half-1
    dst = np.zeros((rows, cols), dtype=np.uint8)
    for y in range(start, end):
        for x in range(start, end):
            a = []
            for i in range(y - half, y + half + 1):
                for j in range(x - half, x + half + 1):
                    a.append(image[i][j])
            # 取中间值
            a = np.sort(a, axis=None)
            if len(a) % 2 == 1:
                medValue = a[len(a) // 2]
            else:
                medValue = int((a[len(a) // 2] + a[len(a) // 2 + 1]) / 2)
            dst[y][x] = medValue
    return dst


image = cv2.imread('Images/saltlena.png')

med = medianBlur(image)

# cv2.imwrite('Images/results/Med_image.png', med)  #写入
cv2.imshow('image',image)
cv2.imshow('Med_image',med)
cv2.waitKey(0)
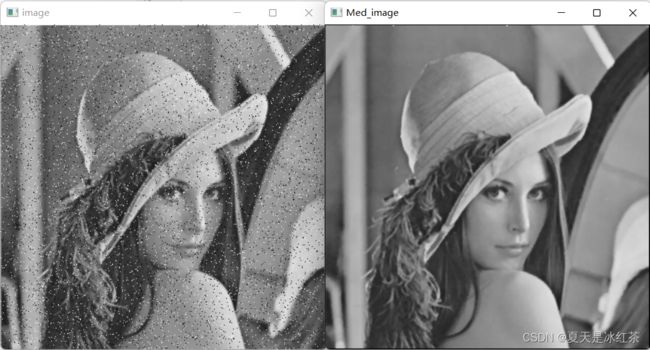
cv2.destroyAllWindows()

中值滤波效果展示：

Opencv代码实现

import cv2
import numpy as np

def stackImages(scale,imgArray):
    rows = len(imgArray)
    cols = len(imgArray[0])
    rowsAvailable = isinstance(imgArray[0], list)
    width = imgArray[0][0].shape[1]
    height = imgArray[0][0].shape[0]
    if rowsAvailable:
        for x in range ( 0, rows):
            for y in range(0, cols):
                if imgArray[x][y].shape[:2] == imgArray[0][0].shape [:2]:
                    imgArray[x][y] = cv2.resize(imgArray[x][y], (0, 0), None, scale, scale)
                else:
                    imgArray[x][y] = cv2.resize(imgArray[x][y], (imgArray[0][0].shape[1], imgArray[0][0].shape[0]), None, scale, scale)
                if len(imgArray[x][y].shape) == 2: imgArray[x][y]= cv2.cvtColor( imgArray[x][y], cv2.COLOR_GRAY2BGR)
        imageBlank = np.zeros((height, width, 3), np.uint8)
        hor = [imageBlank]*rows
        hor_con = [imageBlank]*rows
        for x in range(0, rows):
            hor[x] = np.hstack(imgArray[x])
        ver = np.vstack(hor)
    else:
        for x in range(0, rows):
            if imgArray[x].shape[:2] == imgArray[0].shape[:2]:
                imgArray[x] = cv2.resize(imgArray[x], (0, 0), None, scale, scale)
            else:
                imgArray[x] = cv2.resize(imgArray[x], (imgArray[0].shape[1], imgArray[0].shape[0]), None,scale, scale)
            if len(imgArray[x].shape) == 2: imgArray[x] = cv2.cvtColor(imgArray[x], cv2.COLOR_GRAY2BGR)
        hor= np.hstack(imgArray)
        ver = hor
    return ver

path = 'Images/Colnoiselena.jpg'

img=cv2.imread(path)
imgGray=cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
imgAverage=cv2.blur(img,(3,3))  #尝试改变核的大小
imgMedianBlur=cv2.medianBlur(img,3)  #可以修改核的大小
imgGaussianBlur=cv2.GaussianBlur(imgGray,(7,7),1.8)
imgBilater=cv2.bilateralFilter(img,9,75,75)

imgStack = stackImages(0.6,([img,imgGray,imgAverage],[imgMedianBlur,imgGaussianBlur,imgBilater]))
cv2.imshow("imges",imgStack)
cv2.waitKey(0)

效果图：

在我运行引导滤波的函数时出现了找不到模块的问题：

AttributeError: 'cv2.ximgproc.GuidedFilter' object has no attribute 'shape'

可能是版本号的问题，有的函数可能申请了专利，由于我之前装opencv的时候很麻烦，所以这里我找了别的大佬的代码，大家可以看看。

详细的引导滤波

import cv2 as cv
from matplotlib import pyplot as plt
import numpy as np

R = 16  # 滤波半径
r = 2 * R + 1
s = 1  # 快速引导滤波（如果大于0）


def read(path):
    """读入图片"""
    src = cv.imread(path)
    return src


def To_HSV(image):
    """转化为HSV空间"""
    dst = cv.cvtColor(image, cv.COLOR_BGR2HSV)  # opencv是BGR模式
    H, S, V = cv.split(dst)
    cv.imshow('V', V)
    return H, S, V


def To_BGR(H, S, V):
    dst = cv.merge([H, S, V])
    dst = cv.cvtColor(dst, cv.COLOR_HSV2BGR)
    cv.imshow('dst', dst)
    return dst


def LSE(V):
    V_down = cv.resize(V, (V.shape[1] // s, V.shape[0] // s))
    V_32 = V_down.astype(np.float32)
    V_2 = np.square(V_32)
    dst1 = cv.boxFilter(V_2, ddepth=-1, ksize=(r, r), normalize=True,
                        borderType=cv.BORDER_DEFAULT)  # 盒式滤波（True为归一化均值滤波），效率高之关键,类似积分图
    # print(dst1)

    u_k = cv.boxFilter(V_32, ddepth=-1, ksize=(r, r), normalize=True,
                       borderType=cv.BORDER_DEFAULT)  # 默认为cv.BORDER_REFLECT101，镜像
    u_k_2 = np.square(u_k)

    sigma_k = dst1 - u_k_2  # D（X）= E（X2）- E（X）2
    print('最大方差为：', np.max(sigma_k))  # kesi的取值应与此同量级,以使方差发挥自适应调节作用（ak公式）

    kesi = 10000  # 重要参数（太小则全部保留梯度信息，没有任何平滑(ak==1)；太大则等价于均值滤波了）

    a_k = (dst1 - u_k * u_k) / (sigma_k + kesi)

    b_k = u_k - a_k * u_k
    # print(a_k)

    return a_k, b_k, V_down


def light(a_k, b_k, V_down, V):
    a = cv.boxFilter(a_k, ddepth=-1, ksize=(r, r), normalize=True)
    b = cv.boxFilter(b_k, ddepth=-1, ksize=(r, r), normalize=True)

    I_down = a * V_down + b
    # cv.imshow('I_down',I_down)
    I = cv.resize(I_down, (V.shape[1], V.shape[0]))
    I = np.where(I > 255, 255, I)  # 可用clip函数
    I = np.where(I < 0, 0, I)
    I_ = I.astype(np.uint8)
    cv.imshow('I', I_)
    return I


if __name__ == '__main__':
    path = 'Images/Colnoiselena.jpg'  # 修改为自己路径
    src = read(path)
    cv.imshow('src', src)
    H, S, V = To_HSV(src)

    ak, bk, V_down = LSE(V)

    I = light(ak, bk, V_down, V)

    cv.waitKey(0)
    cv.destroyAllWindows()

 

 

 最后的总结

均值滤波：卷积核越大，图片的失真越明显，图片会更模糊，如果设置核的大小为（1，1），则结果是原始图像。

中值滤波：随着核的增大，图片会更加模糊，核必须是大于1的奇数，如3，5，7等，在这cv2.medianBlur(src,ksize)当中，填写核时填写一个数字，如3，5，7，在这里我们要对比均值滤波的用法。它对于椒盐噪声的图片效果最好。

高斯滤波：随着核的大小逐渐变大，会让图像更加模糊，核的大小（N，N）必须是大于1的奇数，如3，5，7等，sigma表示的是X方向方差。我们常常在边缘检测中用到它。

双边滤波：具有平滑但保持边缘的特性，而且双边滤波常常用在人像美化上，其他的比如上面的几个都会将图片变模糊。

引导滤波：相对于双边滤波最大的优点是在于算法的复杂度与窗口的大小无关，对于处理较为大型的图片时，在效率上有明显的提升，同时引导滤波可以很好的克服双边滤波当中的梯度翻转的现象，它的线性的计数量，可以显著的提高处理的效率。

参考文章

双边滤波——（博主）一蓑烟雨任平生~

高斯滤波——（博主）半濠春水

 Guided Image Filtering - Kaiming He

详细的引导滤波