机器学习之决策树
一、决策树基本介绍
Decision Tree
- 可以解决分类和回归问题
- 监督学习算法
二、决策树工作原理
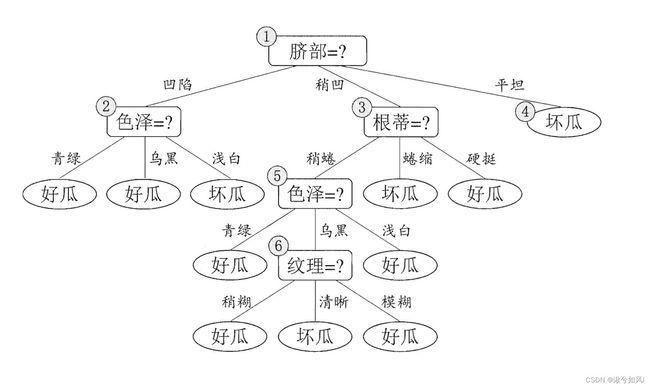
从根开始，按照决策树的分类属性，从上往下，逐层划分。直到叶子节点，便能获得结果。所以决策树算法的核心在于如何构造一颗决策树？
最常见核心的决策树算法有三个——ID3、C4.5、CART
1. ID3
核心思想：以信息增益来度量特征选择，选择信息增益最大的特征进行分裂
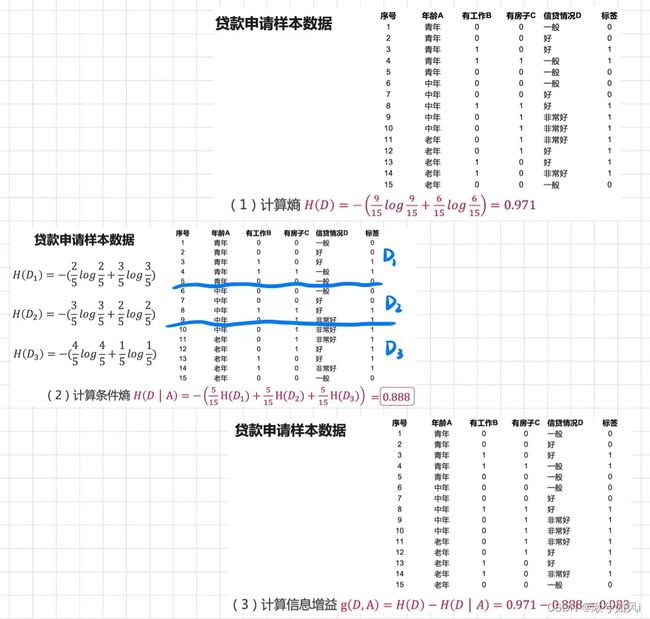
条件熵H(D|A)：已知A条件下的熵。A是训练集中除标签外的一个属性，即根据A属性的不同取值将原训练集D划分成若干子集(D1，D2，D3…)。条件熵是各子集所占比重×子集的信息熵 的加和得出。
条件给的越好，划分出子集的信息熵就越小(因为每个子集基本都是同一分类)，条件熵就越小，信息增益就越大。所以信息增益最大的属性即当前最好的属性。
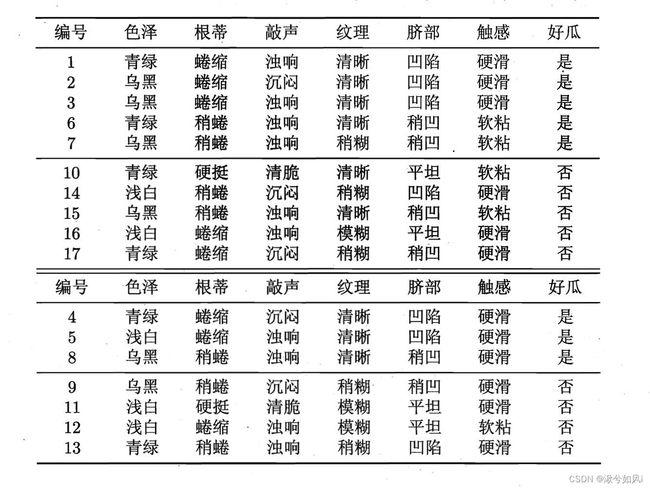
计算示例
缺点
- ID3 没有剪枝策略，容易过拟合
- 信息增益准则对可取值数目较多的特征有所偏好，类似“编号”的特征其信息增益接近于 1；
- 只能用于处理离散分布的特征
- 没有考虑缺失值。
2. C4.5
改进
- 引入悲观剪枝策略进行后剪枝（用递归的方式从底往上针对每一个非叶子节点，评估用一个最佳叶子节点去代替这课子树是否有益。如果剪枝后与剪枝前相比其错误率是保持或者下降，则这棵子树就可以被替换掉）
- 引入信息增益率作为划分标准
- 将连续特征离散化，假设 n 个样本的连续特征 A 有 m 个取值，C4.5 将其排序并取相邻两样本值的平均数共 m-1 个划分点，分别计算以该划分点作为二元分类点时的信息增益，并选择信息增益最大的点作为该连续特征的二元离散分类点
- 对于缺失值的处理可以分为两个子问题： 1. 在特征值缺失的情况下进行划分特征的选择？ （即如何计算特征的信息增益率）2. 选定该划分特征，对于缺失该特征值的样本如何处理？ （即到底把这个样本划分到哪个结点里）
- 针对问题一，C4.5 的做法是： 对于具有缺失值特征，用没有缺失的样本子集所占比重来折算；
- 针对问题二，C4.5 的做法是： 将样本同时划分到所有子节点，不过要调整样本的权重值，其实也就是以不同概率划分到不同节点中。
缺点
- 剪枝策略可以再优化；
- C4.5 用的是多叉树，用二叉树效率更高；
- C4.5 只能用于分类；
- C4.5 使用的熵模型拥有大量耗时的对数运算，连续值还有排序运算；
- C4.5 在构造树的过程中，对数值属性值需要按照其大小进行排序，从中选择一个分割点，所以只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时，程序无法运行。
3. CART
分类标准是基尼系数，其他内容待进一步学习
剪枝
1. 预剪枝
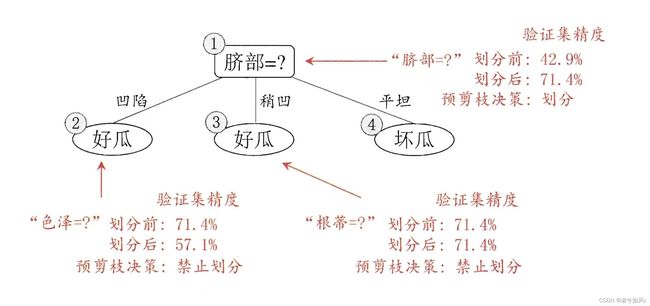
预剪枝使得决策树的很多分支都没有“展开”，不仅降低了过拟合的风险，还显著减少了决策树的训练时间开销和测试时间开销。但可能导致欠拟合。
2. 后剪枝
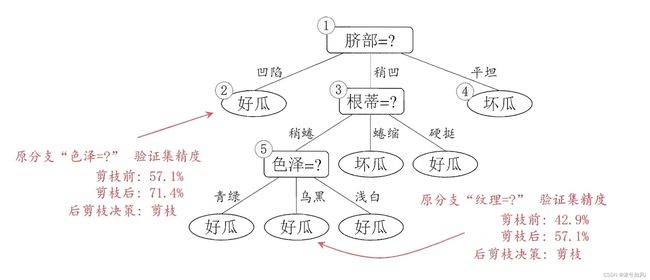
后剪枝通常比预剪枝决策树保留了更多的分支，欠拟合风险很小，泛化性能优于预剪枝。但要自底向上对非叶节点进行逐一考察，因此训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。
三、手写决策树算法核心
# 构造决策树
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet] # 所有分类的数组
if classList.count(classList[0]) == len(classList): # 所有标签都属于一个分类
return classList[0]
if len(dataSet[0]) == 1: # 使用完了所有特征,仍不能将数据集划分成仅包含唯一类别的分组
return majorityCnt(classList) # 若所有属性都被考虑，仍无法划分标签，采用多数表决决定该叶子结点的分类
bestFeat = chooseBestFeatureToSplit(dataSet) # 选取信息增益最大的特征作为下一次分类的依据
bestFeatLabel = labels[bestFeat] # 选取特征对应的标签
myTree = {bestFeatLabel:{}} # 创建tree字典,紧跟现阶段最优特征,下一个特征位于第二个大括号内,循环递归
del(labels[bestFeat]) # 使用过的特征从中删除
featValues = [example[bestFeat] for example in dataSet]
uniqueValues = set(featValues)
for value in uniqueValues:
subLabels = labels[:] # 复制labels列表,避免每次调用createTree()函数将原始列表改变,因为有的调用在前有的调用在后
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) # 循环递归生成树
return myTree
# 使用决策树的分类函数
def classify(inputTree,featLabels,testVec):
firstStr = list(inputTree.keys())[0] # 第一个按照其分类的属性
secondDict = inputTree[firstStr] # 第一个属性下的节点字典,也就是子树
featIndex = featLabels.index(firstStr) # 将标签换为索引
key = testVec[featIndex]
valueOfFeat = secondDict[key]
if isinstance(valueOfFeat, dict): # 如果还是个字典,说明没到叶子结点,继续递归
classLabel = classify(valueOfFeat, featLabels, testVec)
else: # 如果到达叶子结点,直接返回分类标签
classLabel = valueOfFeat
return classLabel
四、sklearn实现决策树算法
1. 分类问题
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
iris = datasets.load_iris() # 加载鸢尾花数据集
X = iris.data[:, 2:] # 只取后两个维度特征
y = iris.target
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy") # 最大深度2,使用信息熵作为划分标准
dt_clf.fit(X, y)
"""
sklearn的决策树实现: CART算法
DecisionTreeClassifier部分参数(默认值)
criterion='gini': 划分标准.默认gini,也可以改成entropy等
max_depth=2: 限制整棵树的最大深度.越大越容易过拟合
max_leaf_nodes=None: 最多有几个叶子结点.越大越容易归你和
min_samples_leaf=1: 对于一个叶子结点,最少应该有几个样本.越小越容易过拟合
min_samples_split=2: 对于一个节点,至少有多少个样本数据,才继续拆分.越小越容易过拟合
"""
# 绘制决策边界
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()
DecisionTreeClassifier()构造函数部分参数及默认值
clf = KNeighborsClassifier(n_neighbors=5,weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2,
metric=’minkowski’,metric_params=None, n_jobs=1, **kwargs)
criterion='gini': 划分标准.默认gini,也可以改成entropy等max_depth=2: 限制整棵树的最大深度.越大越容易过拟合max_leaf_nodes=None: 最多有几个叶子结点.越大越容易归你和min_samples_leaf=1: 对于一个叶子结点,最少应该有几个样本.越小越容易过拟合min_samples_split=2: 对于一个节点,至少有多少个样本数据,才继续拆分.越小越容易过拟合
2. 回归问题
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
# Decision Tree Regressor
from sklearn.tree import DecisionTreeRegressor
dt_reg = DecisionTreeRegressor()
dt_reg.fit(X_train, y_train)
dt_reg.score(X_test, y_test)
# 0.58605479243964098
dt_reg.score(X_train, y_train)
# 1.0
总结
优缺点
1. 优点
- 计算复杂度不高，输出结果易于理解，可解释性强
- 对中间值的缺失不敏感
- 可以处理不相关特征和数据
2. 缺点
- 可能会产生过拟合的问题
- 适用数据类型：数值型和标称型(是或否)
问题
- 书上提到：“预剪枝显著减少了决策树的训练时间开销和测试时间开销‘”。以西瓜的例子来讲，预剪枝需要在验证集计算如果不再以当前属性划分，验证集的精度是多少；如果以当前属性划分，验证集的精度是多少；然后通过两个精度对比，决定是否继续划分。这不是增加了训练时间吗？本来只需要直接划分就好了。是因为如果当前节点不再划分，就没有后续子节点了，所以树的深度小了，所以训练时间开销降低吗？