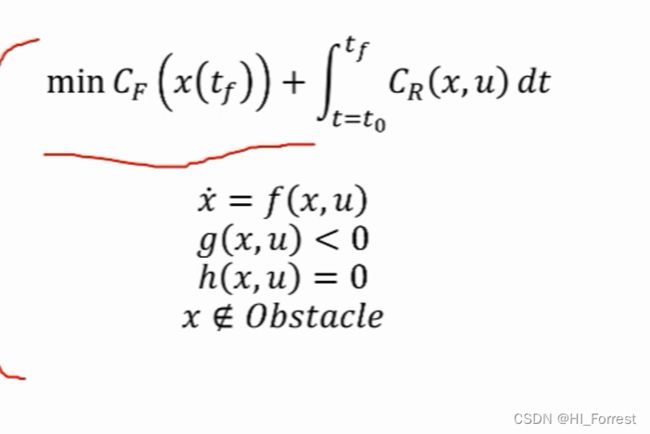运动规划-深蓝学院-高飞

正文

课程视频：运动规划B站
课程资料：运动规划git

一

课程介绍

机器人具备：
状态估计
感知
规划
控制

motion planning ？
安全：无碰撞
柔顺：节能，舒适，某种最优
动力学可行：控制闭环可执行

怎么做研究：

1. 发现问题：
   解决实际问题，不是空想的场景；be engineer ,熟悉机器人；不追热点；诚实实际
2. 解决问题：
   仿真有限，上实物证明算法；

overall knowledge：
不同场景选择合适的方法；设计customized strategy

dirty work :
不要等，动手自己做，实验验证

熟悉整个系统
机器人的所有component都考虑到

outline：

基于搜索
图搜索、dijkstra, A*、跳点
基于采样
PRM, RRT, RRT*, 改进版
考虑动力学的
两点边界值最优控制问题、state lattice， kinodynamic rrt * , hybrid A*

back-end :trajectory optimization
minimum snap

map

栅格地图grid map
八叉树地图 octomap , sparse , structural, 非直接索引递归查询
voxel hashing,
point cloud map
TSDF, truncated signed distance functions
ESDF, euclidean signed distance functions

参考资源

二

基于搜索

在工作空间中，机器人有形状和大小，在配置空间（configuration space）是一个点，易于规划运动。
障碍物膨胀处理，将机器人看为质点。

图：节点和边；有向图和无向图；边的权重/代价；

搜索总是从起始状态点开始，向目标节点形成连接，形成树状结构。

维护一个container容器，存储所有有效节点
循环:
访问容器内的节点，延伸向其邻节点加入容器，

1. 广度优先搜索BFS
   队列，先进先出
   弹出最浅的节点进行延伸，一层一层frontier推进

2. 深度优先搜索DFS
   堆栈，后进先出
   先弹出（选择并延伸）最深的节点（一条路上最后的节点继续延伸）
   先顺时针后逆时针（自己定义一个循环选择策略）

3. 贪心算法greedy beset first search
   根据人为定义的启发式规则（对目标距离的猜测）指引方向
   优先向距离更近的邻节点延伸
   在障碍物环境中陷入局部最优

Dijkstra

策略：累计代价最低的节点先被选择向外延伸
通用循环：弹出-》拓展-》压入堆栈
优先级队列数据结构：自动排序，自动弹出代价最小的节点。
从初始容器弹出节点，延伸新节点加入队列，弹出节点加入另一个容器（被延伸过的）
新节点加入时赋予其由总代价= 父节点代价+父子边代价，如新节点在队列中，比较新旧代价，使队列中节点代价变小。

A*

dijkstra结合贪心：
累积代价gn:当前节点到起点的代价
启发函数hn:当前节点到目标节点的估计代价。
fn = gn + hn
根据fn队列排序，弹出fn最小的节点
新节点的gn是累加的=从起点到该节点的边代价之和，fn是独立的
问题：估计代价并不是实际代价，会影响路径选择。估计代价要小于实际代价，保持最终路径的最优性。
估计代价：欧氏距离，曼哈顿距离

grid based path search

栅格地图结构化highly structural
理想的启发式函数规则

运动规划：前段路径搜索+后端轨迹生成

跳点jump point search

跳点算法
找到搜索的对称性并打破它，找特殊点

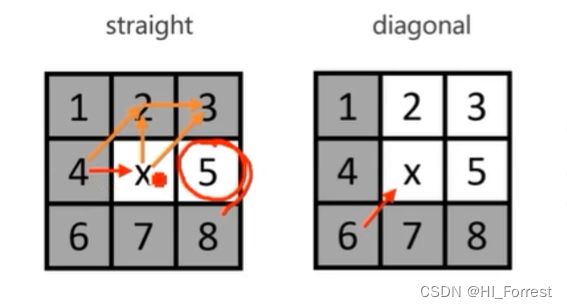
inferior neighbor
natural neighbor
forced neighbor

straight pruning
diagonal pruning

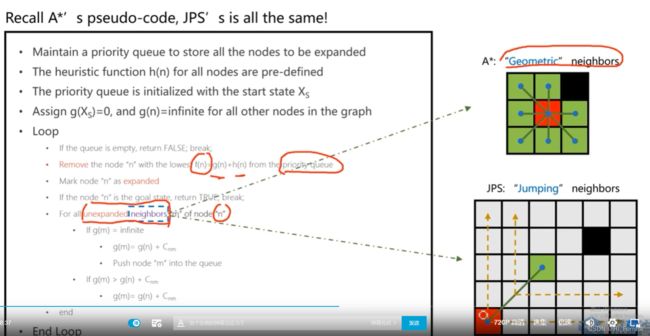
A* 几何邻居加入openlist
JPS 将特殊点加入openlist

采样算法

概率路线图prm

建图阶段：距离准则和障碍物准则
寻路阶段：搜索图中的路径连线

快速搜索随机数 rrt

随机采样Xrand
找树中最近点Xnear
steer延伸一个步长到Xnew
连接Xnear–> Xnew
碰撞检测边的有效性
有则加入树无则（略，减距离加）

优势：快，可行路径

kdtree:

改进Xnear 找最近点的过程

narrow passage:
rrtconnect ，双向搜索
改进采样过程

三

带动力学约束的运动规划

pipeline ： mission - > path finding -> trajectory optimization -> execution

前端考虑动力学，后端轨迹优化难度降低，轨迹优化是局部的

topology，轨迹优化不能改变路径的拓扑结构

考虑动力学和不考虑动力学的路径在地图中是属于不同的拓扑结构，后端的轨迹优化只能在同拓扑结构内优化平滑？不能跳跃到其余拓扑结构中。

state lattice

图搜索是已解决的问题，不再考虑。
不满足于机器人是一个质点。
新的需求：路线图中的边是feasible motion connection， 可行的运动过程。

如何产生executable edge：

1. 正向，离散控制量：
2. 反向，离散状态量：

1. 控制空间的离散sample，a* 等grid search based， control， action， 在某个状态时采取不同的control量， 从而，到达新的状态量。

2. 状态空间离散，sample based， prm , rrt, 先离散采样状态，再产生控制过程去连接两个状态。

1. 从一个状态选取不同的控制量（油门大小，方向盘方向，给系统的输入）车的位置和朝向是状态。
   fixed u，T， 一个时间步内控制量u恒定， T之后积分到下一个状态。简单易于实现，没有任务 导向，规划效率低。

2. 从状态S0 到 S1， 分配时间T， 计算过程控制量u, 有任务导向，难implement，效率高。

状态转移方程，从s0转移到s1 的控制过程。
现代控制理论！
幂零矩阵？

state lattice 第一层需要考虑初始状态和速度，第一层的过程不一样，之后的状态转移控制过程都一致，外层间的过程一样。

boundary value problem

状态空间采样后，计算可行的连接控制过程。

庞特里亚金极小值原理？
costate 协态变量， 哈密尔顿函数。

final state 的惩罚（误差函数）
+
transition cost 过程代价函数

启发函数:
无碰撞，考虑动力学可行，两个代价函数结合。

hybrid a*

dense lattice costs too much time .
prune nodes using grid map.
栅格法剪枝，每格留一个最优（代价最低，control cost, 不只是欧氏距离代价）节点。

1. 欧氏距离
2. 非完整约束动力学约束及无碰撞
3. 质点模型欧氏距离+动力学非完整约束无碰撞

控制空间采样离散低效率，加入one shot 状态空间采样（终点）直接求解某已有状态到终点的最优控制问题。

kinodynamic rrt*

状态空间采样，解（最优）两点边界值问题（O）BVP，形成状态之间的连接，构成搜索树。

四

无人机的运动规划12个状态量，微分平坦为4个量的规划过程。对姿态只有偏航角需要规划，
线速度角速度都用【x,y,z,theta】的微分表示。
参考论文2011 ICRA

无人机的规划过程：

minimum snap

多项式轨迹

boundary condition，初始终止 位置，速度，加速度确定
六变量用五次多项式六参数。

多段轨迹连续：
带速度通过via point
速度不能指定，而是用优化方法确定一个最优的速度加速度值。

段数越多，多项式次数可以降低：

代价函数J：

矩阵形式的约束
首位的位置速度加速度加加速度等式约束。
中间点的位置约束
相邻两段轨迹的速度加速度加加速度的连续约束。
fk’(tf) = fk+1 ’ (t0)

典型凸优化问题,二次规划问题
hessian 矩阵对角矩阵

disciplined convex optimization programs
tools :
linear programming;
quadratic programming;
quadratically constrained qp;
second order cone programming;
semidefinite programming;

formulation .

close form solution

decision variable mapping.
将多项式系数映射到端点物理参数。

重要

implementation

1. solver :
   cvx
   mosek
   ooqp
   glpk

2. numerical stability
   全局时间轴太长造成数值计算不稳定，高阶多项式。

方案：每段轨迹归一化到时间0-1， 求出多项式后再进行放缩。

四

minimum snap 只约束了way point上的约束，中间过程没有约束（障碍物信息不考虑，只优化指标）

硬约束，满足约束subject to 。
软约束，最优化指标函数，倾向于满足约束范围。不一定严格满足。

轨迹优化 硬约束

corridor-based trajectory optimization

栅格化自由空间，栅格膨胀简化。
轨迹连接点处于两个栅格的重叠区域，满足走廊约束。

instant linear constraint：
首位状态约束；中间点约束；连续性约束。

interval linear constraint：
边界约束boundary constraint；
动力学约束 速度加速度连续可达。

problem：
way point 上面满足约束，如何保证全局满足约束？
iteratitvely check 检查轨迹极值是否超出约束，超出则添加中间点使轨迹被压入约束内。
检查极值点是否超出约束？
多项式求极值问题，伴随矩阵的秩 求多项式根。
eigenvalue.

bezier curve optimization

贝塞尔曲线，way point 作为控制点，全局满足约束 bernstein.
一定起始于起点，终止于最后一个点，中间控制点不通过。
贝塞尔曲线的凸包性质，贝塞尔曲线各段，都在控制点构成的凸包内，因此不会发生碰撞。

位置贝塞尔，速度贝塞尔曲线。
边界约束；
连续性约束，前后段的尾首控制点相同，则连续。

dense constraint

稠密约束

mixed integer optimization

软约束

硬约束：障碍物和自由空间两种平均分布的空间，自由空间内没有障碍物距离概念，对感知反馈的噪音敏感。

软约束：考虑到障碍物的距离

vision based drone：
感知范围有限，有噪音。

planning strategy

五

多路径，最优路径的选择

MDP based path planning

uncertainty in planning

markov decision process 马尔科夫决策过程

目前的假设：
执行是完美无误差的，没有扰动
完美的反馈，状态估计准确

实际上：存在uncertainty

planning with uncertainty

1. decision maker （game player）
   1.1 robot
   1.2 nature
2. nature + robot actions = ？
   代价函数 衡量 nature 参与下 robot 动作的 共同结果
   1. nature的动作对机器人是未知，假设是最差的扰动。
   2. 在概率模型下，nature的动作可预测=动作的期望

cost function is a metrics that evaluate all possible plans(or paths)

Markov Decision Process

S / X state space
A / U action space
P state transition function under probabilistic model
R / L immediate reward / negative one-step cost

theta: nature 的action, 隐式函数或者显式定义值。
l：cost function， 简单定义为 欧式距离

worst case analysis for nondeterministic model
最小化最差情况代价

expected case analysis for probabilistic model
最小化期望代价

Solving MDP

RTDP 实时动态规划

计算代价（cost to go ）需要小于等于实际代价

• 流程：

1. 初始化所有状态点的G值（cost value）
2. 按greedy policy 随机选取输出
3. backup 所有经过的点
4. 重复迭代，所有状态的bellman error 小于阈值

• 例子
  X 初始化范围
  Xl, Xf, 初始状态和目标状态
  U robot的动作，上下左右
  θ nature的动作。uncertainty意外的几率。
  cost function ： 每一步的代价 一样 都是 -1
  goal ： find an optimal plan from Xl to Xf.

decision making, 和强化学习。

minimax cost

不确定性的规划中，在机器人在某确定状态下实施动作，由于nature 的动作影响，其输出状态不确定。

minimize (max (cost to go)) of all states.
状态维度爆炸，难直接求解

• 动态规划：

在Uk集合中选择最好的动作，使得Xi 在最坏的θ 环境动作下，最小化cost到达Xf.

robust to uncertainty
overly pessimistic
harder to compute than normal paths

expected cost

probabilistic model

六

MPC 模型预测控制

1. 模型model
   系统模型：运动学公式
   问题模型：最优化指标函数
2. 预测prediction
   状态空间
   输入空间（控制空间）
   参数空间
3. 控制control
   选取最优的control process
   

optimization

图搜索
随机搜索
凸优化：二次规划
非凸优化：连续二次规划
粒子群优化（非凸，非线性，不连续的）

设定初末状态
设置测量反馈模块
解优化问题求控制量
输入控制量控制系统

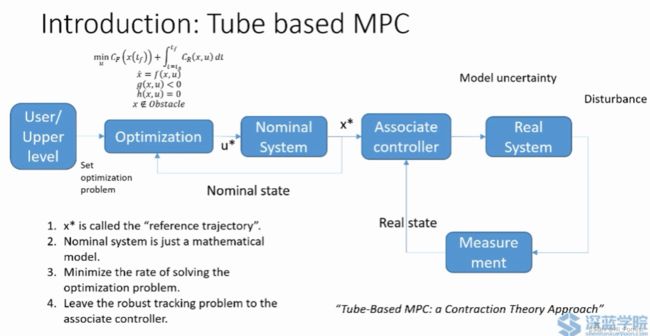
tube based MPC

控制量输入nominal system（优化的系统模型），产生了参考理想轨迹（没有外界扰动），真实系统通过一个associate controller 来处理反馈量和外界扰动，跟随理想轨迹。