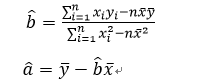线性回归，最小二乘法 C语言实现

1.  前言

最近断断续续重温了一些数学书，有高等数学，也有初等数学。有时候，觉得数学才是世界上最美的东西，但有时候又觉得数学很高冷，不接地气。

不过，前段时间工作中用到了最小二乘法，下面记录一些用法。

2. 最小二乘法

根据维基百科的说明：
最小二乘法 （又称 最小平方法 ）是一种 数学 优化 技术。
它通过最小化 误差 的平方和寻找数据的最佳 函数 匹配。
利用 最小二乘法 可以简便地求得未知的数据，
并使得这些求得的数据与实际数据之间误差的平方和为最小。

看了之后一头雾水对不对，是的，任何人看着一段不知道在说啥。下面举个例子，就很好懂了。

针对线性最小二乘法即直线拟合，如下图（来自维基百科）所示：

透过这张图，我想大家一定能理解，我们用最小二乘法来做什么事情，即： 

根据已有的数据（图中的点），来做出一条最贴近数据发展趋势的直线。

通过这条直线，我们可以对未来的数据进行预测，因为基本会落在这条直线附近。

当然了，最小二乘法不只是直线，还可以是曲线，本文不讨论。

3. 求解直线方程
我们现在要做的，就是求解直线方程。

假设已知有N个点，设这条直线方程为：  y = a·x + b

其中，a和b的计算公式如下：

简化后：

本文对于推导过程不在赘述，网上都有。

4. 算法代码和效果演示

#include 
#include 

#define     COUNT     18.0
int main()
{
    //float x[6]={0.0,1.0,2.0,3.0,4.0,5.0};
    //float y[6]={1.1,1.9,3.1,3.9,4.4,4.9};
    /*float x[6]={0.0,1.0,2.0,3.0,4.0,5.0};
    float y[6]={0.0,1.0,2.0,3.0,4.0,5.0};*/
    float x[18]={0};
    float y[18]={560,560,560,560,558,560,556,547,545,548,545,547,547,547,547,547,555,558};


    float a,b,mxy,xx,yy,x2,x22;
    int i;

    a=b=mxy=xx=yy=x2=x22=0.0;

    for(i=0;i

结果：

Y=-0.68x+558.39

sh: 1: pause: not found