蒙特卡洛树搜索 MCTS 入门

引言

  你如果是第一次听到蒙特卡洛，可能会认为这是一个人名。那么你就大错特错，蒙特卡洛不是一个人名，而是一个地方，还一个赌场名！！！但是这不是我们的重点。

  我们今天的主题就是入门蒙特卡洛树搜索，这个算法我个人觉得非常神奇也非常有意思。因为前几年 AlphaGo 就是借助蒙塔卡洛树搜索以及基于深度学习的的策略价值网络击败了人类冠军，赢得了胜利。而今天我们的主角就是蒙特卡洛树搜索它究竟是怎么实现的？它的原理？以及会举出一个例子来告诉大家整个算法的工作流程。

---

一、什么是 MCTS？

  蒙特卡洛树搜索是一类树搜索算法的统称，简称 MCTS（ Monte Carlo Tree Search）。它是一种用于某些决策过程的启发式搜索算法，且在搜索空间巨大的游戏中会比较有效。那什么叫做搜索空间巨大呢？比如说，在上世纪90年代，IBM公司推出深蓝这个 AI，击败了当时国际象棋的世界冠军，而这个 AI 也比较简单粗暴，把整个国际象棋的搜索空间全部穷举出来，把整个游戏树全部列举出来，那么不管对手下什么，它都知道下一步怎么下可以把他下赢。而对于围棋这种游戏，围棋棋盘是 19*19 的，也就是说有 361 个落子的位置，那么如果我们想把所有围棋的棋局的可能列举出来，一般来说就是 361！，这个数量是比宇宙的原子数量还要多的，就算是世界上最强的超级计算机也无法把所有的可能性穷举出来，那么我们就需要用到类似于蒙特卡洛树搜索这样的稍微智能一点，更可行的办法去对围棋这个游戏可以进行棋盘式的搜索，然后进行决策，最后下赢人类选手。

  从全局来看，蒙塔卡洛树搜索的主要目标是：给定一个游戏状态来选择最佳的下一步。

  MCTS 受到关注主要是由计算机围棋程序的成功以及潜在的众多难题上的应用所致。超越博弈游戏本身，MCTS 理论上可以被用在以（状态 state，行动 action）对定义和用模拟进行预测输出结果的任何领域。

  常见应用包括 Alpha Go，象棋或围棋 AI 程序等等。

---

二、算法过程

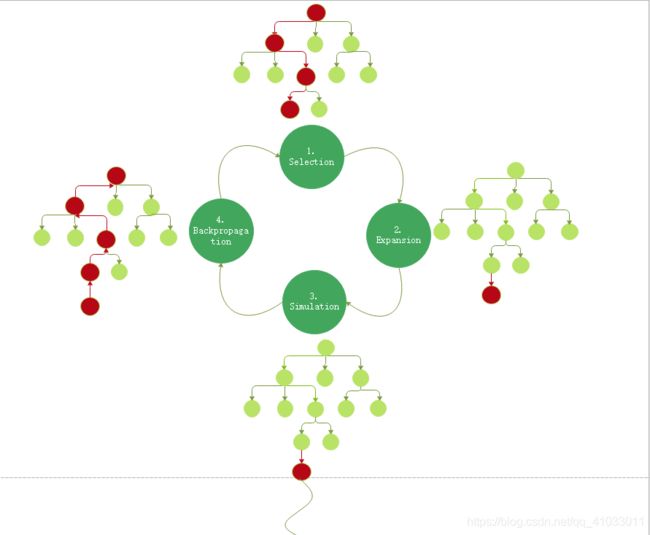
算法过程一般有四步：

• 选择（Selection）：选择能够最大化 UCB 值的结点
  
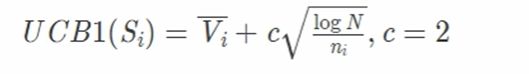
• 扩展（Node Expansion）：创建一个或多个子结点
• 仿真（Simulation）：在某一结点用随机策略进行游戏，又称 playout 或 rollout
• 反向传播（Backpropagation）：使用随机搜索的结果来更新整个搜索树

  在完成了反向传播这一步，我们就会持续迭代，回到选择这一步，然后再进行扩展仿真，然后再反向传播，再回到选择扩展仿真，不断地迭代下去，直到算法结束并且给出最终决策。

  下面，我将用一个流程图简单展示一下上面四个步骤：

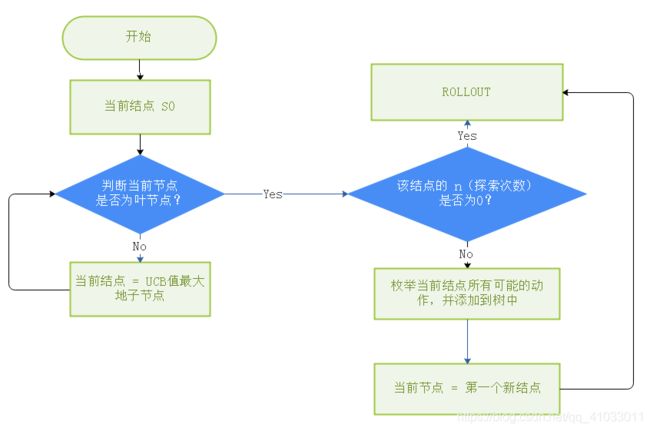
当然你可能看上面的流程图会有点迷。不要慌，下面我用一个中文流程图展示一下整个算法的流程。

  整个算法过程是这样的。一开始，我们会找到根节点 S0，代表目前的游戏的一个状态，那么接下来判断它是否是叶节点，如果它不是叶节点，是一个中间节点的话，我们就计算出该结点下面的所有子结点的 UCB 值并且找到 UCB 值最大的子结点，然后将这个 UCB 最大值的子结点当作当前节点进行下一步迭代，继续判断当前结点是否是叶节点，若它还不是叶节点，我们就在这个结点下面计算它的所有子节点的 UCB 值并找出最大的结点当作当前结点继续进行迭代，直到找出一个结点是叶节点，我们就判断该节点的 n（探索的次数） 是否为 0，如果它的探索次数为 0，那么就代表该结点是没有被探索过的，那么我们就进行 ROLLOUT，如果不是 0，我们就枚举出当前结点所有的动作，并添加到树中，这一步相当于是 Node Expansion，然后我们将第一个新结点作为当前结点，然后进行 ROLLOUT。

下面我将对算法的四个步骤做进一步的论述。

1. 选择（selection）

下面我对选择中 UCB 公式中的各项做一个解释。

• Vi：该结点下的平均 Value 大小，比如说，好的一步它的 Value 更大一些，差的一步相对来说要小一些
• c ：常数，通常可以取 2，相当于是加号两边式子的一个权重
• N：总探索次数，就是对所有的结点一共 explore 了多少次
• ni：当前结点的探索次数

2. 扩展（Node Expansion）

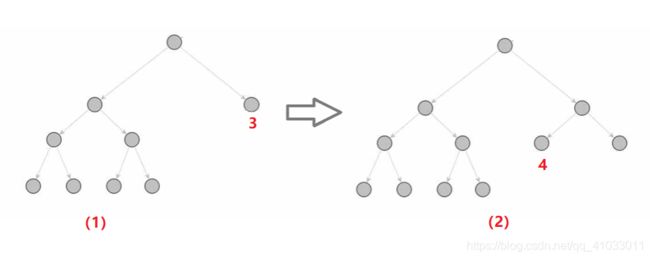
下面通过一个例子来说明。

  比如我们从根节点出发，它不是叶子节点，之后计算它的两个子节点的 UCB 值，比如说结点 3 的 UCB 值更大，但是它之前已经被访问过了，根据我们之前的流程图，该节点不会直接进行 ROLLOUT，而是枚举出当前节点所有可能的动作并添加到树中，那么我们枚举出了结点 3 可能有两个动作，所以形成了图(2)，然后接下来我们再看我们要采取哪种动作，这就是 Node Expansion。

3. 仿真（Rollout）

  接着上面一步，根据我们的流程图，会将第一个新结点（结点 4）作为当前结点，会对它进行一个 Rollout。

  那么这个 rollout 怎么做呢？它会进行一个随机检测，下面我用一段伪代码来表示 rollout 过程：

def Rollout(S_i): # S_i：当前状态
	loop forever: # 无限循环
		if S_i a terimal state: # 如果当前状态是个终止状态，比如说你赢了或者他赢了
			return value(S_i)   # 返回对 S_i 这个状态的价值，比如说你赢了，这个价值可能就会相对比较高
		
		# 假设还没到终止状态
		A_i = random(available_action(S_i)) # 随机选取当前状态下能够采取的一个动作
		S_i = simulate(A_i, S_i)   # 通过当前状态 S_i 与随机选取的动作 A_i 来计算出下一步的状态并赋值给 S_i

  下面我再用图示进行说明。

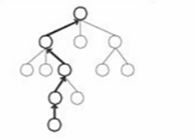
  来看下面这张图，假设我们从黄色节点 1 进行 Rollout，它随机决策到结点 2，然后再随即决策到结点 3，然后在随机决策一直到最后红色结点 7，该节点的状态是 terminal state，然后得到一个 value，然后再将 value 返回给黄色节点 1。

  这一步其实也是蒙克卡罗树搜索的非常重要的一关，因为这一步很像是在用随机的方法去逼近整体的一个分布，你想，如果黄色节点 1 代表的是更好的一个动作的话，那么赢的概率就会更大一点。经过很多次的仿真，都会得到一个比较大的概率值，如果它是一个不好的策略，那么经过很多次的仿真，大概率是不会得到一个很好的概率。

4. 反向传播（Backpropagation）

  在完成了 Selection，Expansion 和 Rollout 之后，我们再进行 Backpropagation。它是做什么的呢？

  在 Rollout 中我们计算出了 value 之后，我们需要返回这个 value，那么对于它所有的父节点（下图黑线上的所有的结点），它们的探索次数全部 +1，它们的 value 也会进行一个累加，然后我们整个算法会 repeate 很多次，直到蒙特卡洛树能够给出当前状态下最好的一个解答，就是我到底应该怎么走。

  那么四个步骤到此就结束了，但是之前提到过这个算法会一直进行迭代，那么这个算法到底什么时候结束？

---

算法何时终结？

  一般的方法比如说游戏内棋手的限制时间，比如说，像围棋，国际象棋，在比赛当中每个棋手的时间都是有限制的，但是如果你用电脑肯定就有无限的时间，你可以将其全部穷举出来，但是这样是没有意义的。所以我觉得一个 AI 能够在规定时间内，尤其是时间越少越好，能够在更少的时间内做出更好的决策说明这个机器才更加的智能。如果给你无限的时间来做出一个决策，你可以暴力穷举出所有的可能性，其实就说明这个 AI 没有那么智能。所以一般来说我们会在规定时间范围内终结算法的迭代，然后给出最优的一个解答，下一步应该怎么走，然后再让对面去下棋，对面下完之后，你再进行一个搜索在规定时间内给出一个最优的。

  还有一种就是固定迭代的次数。比如说，第一个 AI 迭代了 5000 次得到了一个比较好的结果，另一个 AI 用了 50 次就迭代出了一个比较好的结果，那么就基本认定第二个 AI 相对来说是比较智能的。所以我们也可以给出一个固定的迭代次数，比如说你算到 5000 次迭代就让蒙特卡洛树搜索停下来给出一个决策。

  至于怎么给出一个决策呢？很简单，在迭代完成后，选择 value 更大的结点即可完成决策。

---

举例说明

  下面举出一个例子来详细说明蒙特卡洛树搜索的过程。

  首先我们有一个根节点，S_0，它有两个属性值 T_0（价值），N_0（迭代的次数）。

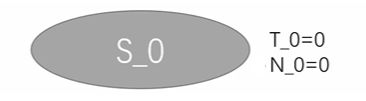
  那么我们首先先判断 S_0 是否是叶节点，它确实是一个叶节点，我们需要对它进行一个 Node Expansion，我们发现有两种策略可以采取分别为 S_1 和 S_2。

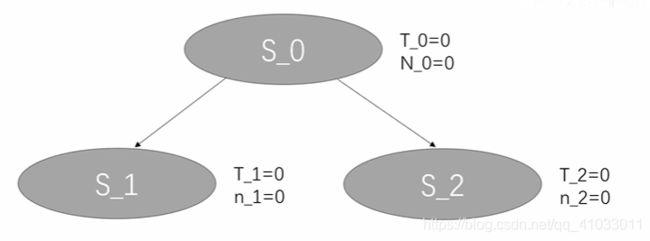
  在这里，我们可以直接选择 S_1 作为当前节点，也可以通过 UCB 公式计算一下 S_1 和 S_2 的 UCB 值，并选取其中 UCB 值较大的节点作为当前节点。下面我们在列出 UCB 的公式：

  可以发现 S_1 和 S_2 的 ni 都是 0，那么对于 S_1 和 S_2 来说，它们的 UCB 值都是无穷大，所以选择谁都是一样的，那么我就根据我上面画的流程图，选择第一个新结点作为当前节点，即 S_1。

  然后我们发现 S_1 的 n_1（探索次数）为 0，即它没有被探索过，根据之前的流程图就应该进行 Rollout。

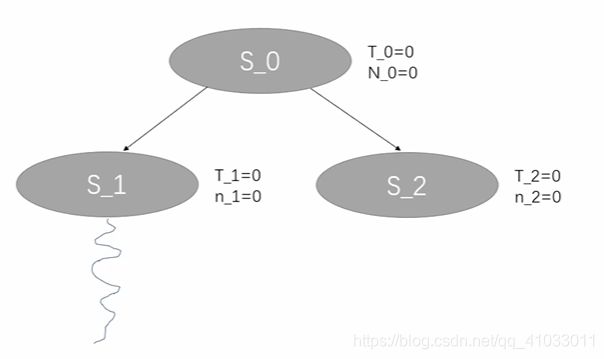
  结果我们发现 value = 20，在 Rollout 完成之后，我们对 S_1 进行 Backpropagation，将 S_1 的 T_1 更新为 20，n_1 更新为 1，然后再反向传播到它的父节点 S_0，并更新S_0 的 T_0 为 20，N_0 为 1。那么就完成了第一轮迭代。

  每一次迭代，都需要从根节点开始。所以到了第二轮迭代，我们同样首先判断 S_0 是否是叶节点，S_0 不是叶节点，然后我们使用 UCB 对它进行一个 Selection，选择下一个节点，S_1 的迭代次数为 1，而 S_2 的迭代次数还是 0，所以 S_2 的 UCB 还是无穷大，所以下一个节点选择 S_2，然后判断 S_2 是否是叶节点，它是叶节点，并且还未被探索过，那么直接对 S_2 进行 Rollout，然后我们得到 value = 10，然后进行 Backprppagation，更新 S_2 的 T_2 为 10， n_2 为 1，然后更新 S_2 的父节点 S_0，将 S_0 的 T_0 更新为 30（20+10），N_0 为 2（1+1），那么就完成了第二次迭代。

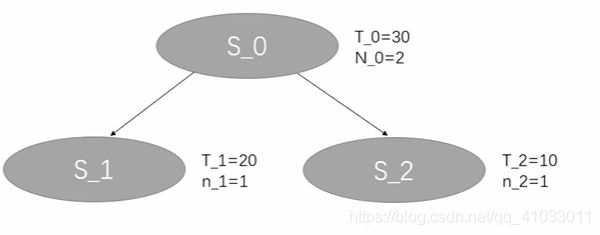
  接下来，我们继续迭代，我们还是从 S_0 开始，它不是叶节点，然后计算 S_1 和 S_2 的 UCB 值。

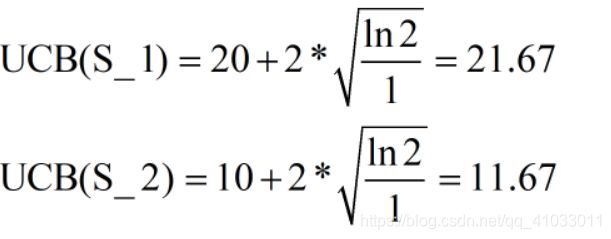
  因为 S_1 的 UCB 大于 S_2，所以我们选择 S_1，S_1 是一个叶节点，并且它的探测次数不为 0，那么我们就枚举出当前节点所有可能的动作，并添加到树中，即 Node Expansion。那么假设 S_1 也有两个动作 S_3 和 S_4。

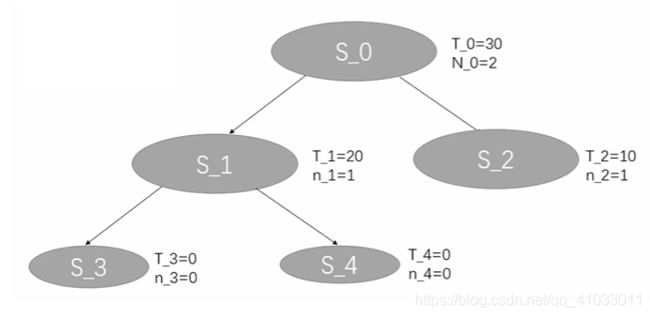
  因为 S_3 和 S_4 它们的探索次数都为 0，所以 UCB 都为无穷大，所以我们还是选择第一个新结点 S_3 作为当前节点，然后对 S_3 进行 Rollout，最终我们得到的 value = 0，然后对它进行一个反向传播，更新 S_3 的 T_3 为 0，n_3 为 1，更新 S_1 的 n_1 为 2，T_1 不变，更新 S_0 的 N_0 为 3，T_0 不变。这就是我们的第三次迭代。

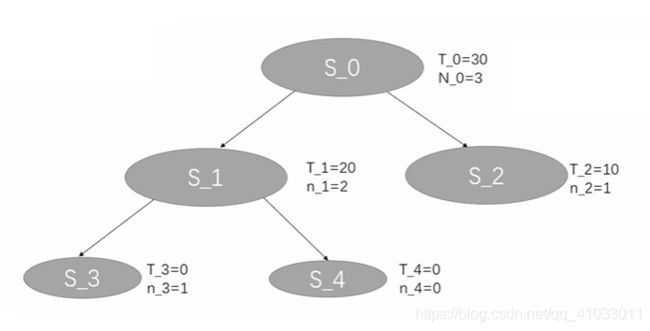
  然后我们进入第四次迭代，还是从 S_0 开始，它不是叶节点，然后根据 UCB 公式计算我们选择 S_1 还是 S_2，此时我们需要注意的是，在 UCB 公式中，Vi 是 value 的平均值，所以在 S_1 中，S_1 已经被探索了 2 次，所以 S_1 的平均 value 为 10（20/2=10），那么 S_1 和 S_2 的 UCB 计算如下：

  所以我们下一个节点选取 S_2，S_2 为叶节点，而且已经被探索过了，所以需要枚举出所有的动作并添加到树中，还是假设 S_2 有 2 个动作 S_5 和 S_6，然后我们选择 S_5 对其进行 Rollout，得到 value = 15，然后依次更新 S_5，S_2, S_6 相应的 T 和 n，然后又完成了一次迭代。

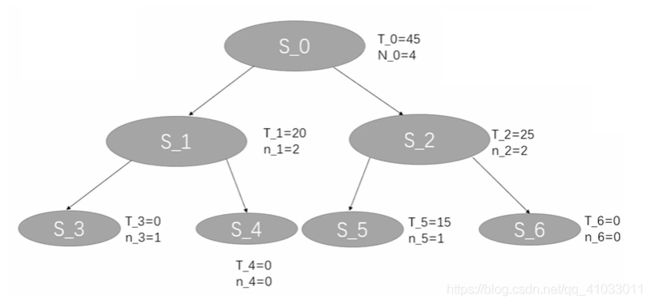
  假如我们现在就停止迭代，那么我们看一下我们究竟应该选 S_1 还是 S_2，很明显，S_2 的 T_2 （value）会更大一些，所以说我们通常会选择 S_2，也就是做第二个动作，是目前这个树当中最优的解。

  那么，关于 UCB 公式还有几个需要注意的点。如果说 Vi 越大，那么 UCB 相应的也是越大的，而 UCB 越大代表越有可能选择这条路径，Vi 越大代表这个节点平均的价值会更高，我们就更愿意去搜索它。但是如果说只有 Vi 可不可以呢？比如将 UCB 公式变成这样：

  当然不行，如果这样的话那些没有被探索过的节点就永远不会被探索，这就是为什么会有右边这一项，特别是当 ni 等于 0 的时候，UCB 会等于无穷大，那么就一定会去探索这个没有被探索过的节点，那么随着 N 的一些变化，相应的 UCB 也会跟着变化。总之，这个 UCB 公式既保证了探索了的分支可以再次被探索，又保证了我们尽量去探索那些价值更大的那些路径然后让我们能够更好的完成整个游戏。

---

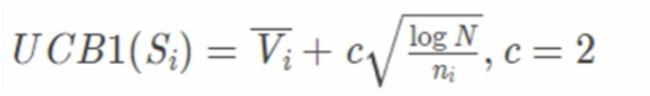
  以上就是我对蒙特卡洛树搜索的初步理解，如有错误，还请指正~~