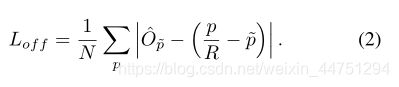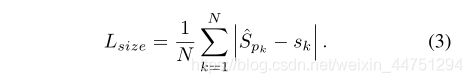论文阅读笔记 | 目标检测算法——CenterNet算法
如有错误,恳请指出
文章目录
- 1. Introduction
- 2. Preliminary
-
- 2.1 keypoint detection loss
- 2.2 offset loss
- 2.3 size loss
- 2.4 overall loss
- 3. Objects as Points
- 4. Result
paper:Objects as Points
Source code:https://github.com/xingyizhou/CenterNet
思想:
目标检测将对象识别为图像中与轴对齐的框。大多数成功的物体检测器都列举了几乎详尽的潜在物体位置列表,并对每个位置进行分类,这是比较浪费时间的一种做法,而且需要额外的后处理方法。
在CenterNet中,作者将对象建模为单个点,即其边界框的中心点。我们的检测器使用关键点估计来找到中心点,并回归到所有其他对象属性,如大小、三维位置、方向,甚至姿势。与相应的基于anchor的检测器相比,具有端到端的可区分性、更简单、更快速和更精确。
1. Introduction
当前的目标检测是通过用一个边界框来紧密包围对象从而表示它,然后将对象检测简化为大量潜在对象边界框的图像分类。对于每个边界框,分类器确定图像内容是特定对象还是背景。
对于one-step网络来说,通过滑动窗口生成一些列密集的anchor,然后直接对这些anchor进行分类预测,近年来的改进方向包括anchor的比例形状(yolo系列),不同尺度进行特征融合(FPN系列)以及不同样本见的损失权重改进(RetinaNet)。而对于two-step网络来说,会对anchor先进行一个nms挑选,所以其训练比较麻烦不能实现端对端预测。
CenterNet中,会用一个中心点去代表检测对象。然后对象的其他属性(对象大小、尺寸、三维范围、方向和姿态等等)则直接从中心位置的图像特征进行回归。也就是将目标检测问题简化成一个关键点检测问题。

主要的流程如下:
将图像简单的喂入一个卷积神经网络得到一个heatmap,heatmap的峰值(peaks)对应与物体的中心,每个峰值处的图像特征预测对象边界框的高度和宽度。当进行检测时,只需要简单的进行前向传播实现,不需要NMS等后处理方法,所以可以实现端对端检测。
1. CenterNet与其他基于anchor算法的区别:
CenterNet与基于anchor的One-step算法密切相关,因为一个中心点可以看作是一个形状不可知的anchor,但存在一些区别:
1)CenterNet通过根据位置(peaks)分配anchor,而不是在特征图上进行密集覆盖,不需要手动的设置前景或背景的阈值。
2)CenterNet中的每一个对象只有一个正样本的anchor,所以不需要非极大值抑制处理,也就是不需要后处理方法,只需要提取关键点heatmap中的局部峰值。
3)与传统的对象检测器相比,CenterNet使用了更大的输出分辨率,这消除了对多个anchor的需要

2. CenterNet与其他关键点检测算法的区别:
CenterNet不是关键点检测的首次使用。CornerNet使用对象的左上角与右下角作为两个关键点,而 ExtremeNet使用对象的四个角点与中心点五个点作为关键点。这两种方法都建立在与CenterNet相同的鲁棒关键点估计网络上。
但是这两种关键点检测算法,在关键点检测之后需要一个组合分组阶段(以CornerNet为例,由于分了两组heatmap分别检测左上角与右下角,需要一个额外的embedding计算这两组之间的距离,距离相识则被匹配为一组),这大大降低了每个算法的速度。
而在CenterNet中,只需为每个对象提取一个中心点,而不需要分组或后处理。
2. Preliminary
2.1 keypoint detection loss
若以 I ∈ R W × H × 3 I ∈ R^{W \times H \times 3} I∈RW×H×3表示一张输入的图像的宽为W,高为H。然后我们的目标是制作关键点的heatmap: Y ^ ∈ [ 0 , 1 ] W R × H R × C \hat{Y} ∈ [0, 1]^{\frac{W}{R} \times \frac{H}{R} \times C} Y^∈[0,1]RW×RH×C,其中R表示输入步幅(也可以理解为缩放因子,也就是下采样的倍数,这里默认是4,也就是输出分辨率会输出4倍),C是关键点类型的数量。如果目标检测的任务中有80类对象,那么输出的heatmap的通道数就是80,每层channel表示一类对象的heatmap。如果预测得到: Y ^ x , y , c = 1 \hat{Y}_{x,y,c} = 1 Y^x,y,c=1,则表示C类目标中的 ( x , y ) (x,y) (x,y)位置检测到关键点,否则 Y ^ x , y , c = 0 \hat{Y}_{x,y,c} = 0 Y^x,y,c=0则是背景。作者使用了多种backbone从输入图像得到heatmap Y ^ \hat{Y} Y^。
对于每一类C的每一个真实对象(ground truth)的关键点表示为: p ∈ R 2 p ∈ R^{2} p∈R2,而这个真实对象的关键点映射在一个低分辨率的特征图上为: p ~ = ⌊ p R ⌋ \widetilde{p} = \lfloor \frac{p}{R} \rfloor p =⌊Rp⌋ (向下取整,所以也存在损失)。然后,将所有ground truth关键点投影到heatmap上: Y ∈ [ 0 , 1 ] W R × H R × C Y ∈ [0, 1]^{\frac{W}{R} \times \frac{H}{R} \times C} Y∈[0,1]RW×RH×C,使用高斯核得到最后结构: Y x y c = e x p ( − ( x − p ~ x ) 2 + ( y − p ~ y ) 2 2 σ p 2 ) Y_{xyc} = exp(- \frac{(x - \widetilde{p}_{x})^{2} + (y - \widetilde{p}_{y})^{2}}{2\sigma^{2}_{p}}) Yxyc=exp(−2σp2(x−p x)2+(y−p y)2)。其中 σ p σ_{p} σp表示对象的尺寸自适应标准偏差。
一个补充的说明,heatmap是通过把ground truth从输入图片位置映射到该较低分辨率的图上,然后再以ground truth为中心做高斯分布 Y x y c = e x p ( − ( x − p ~ x ) 2 + ( y − p ~ y ) 2 2 σ p 2 ) Y_{xyc} = exp(- \frac{(x - \widetilde{p}_{x})^{2} + (y - \widetilde{p}_{y})^{2}}{2\sigma^{2}_{p}}) Yxyc=exp(−2σp2(x−p x)2+(y−p y)2)来为整个图赋值,即以ground truth为中心,在其一定半径内的点的Yxyc值如瀑布式下降(高斯分布)。
关键点预测损失公式为:
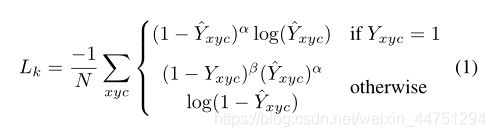
α和β是focal loss超参数,这里沿用CornerNet中的设置,α = 2 , β = 4 。N则为图片中总的keypoint数量。
2.2 offset loss
上诉所提到的,当关键点在原图到一个低的分辨率特征图时采用了向下取整所以会造成一个偏移损失。正如原文所说,为了恢复由输出步幅引起的离散化误差,我们还对每个中心点预测了局部偏移: O ^ ∈ R W R × H R × 2 \hat{O} ∈ R^{\frac{W}{R} \times \frac{H}{R} \times 2} O^∈RRW×RH×2.
所有c类共享相同的偏移预测。偏移是用L1损失训练的.监督仅作用于关键点位置,所有其他位置都被忽略。
2.3 size loss
C类的目标k的四个边界坐标可以表示为: ( x 1 k , y 1 k , x 2 k , y 2 k ) (x^{k}_{1},y^{k}_{1},x^{k}_{2},y^{k}_{2}) (x1k,y1k,x2k,y2k),那么其中心点的坐标就可以表示为: p k = ( x 1 k + x 2 k 2 , y 1 k + y 2 k 2 ) p_{k} = (\frac{x^{k}_{1} + x^{k}_{2}}{2},\frac{y^{k}_{1} + y^{k}_{2}}{2}) pk=(2x1k+x2k,2y1k+y2k)。我们用关键点估计法来预测所有的中心点。此外,我们回归到原图每个对象k的长宽尺度大小: s k = ( x 2 k − x 1 k , y 2 k − y 1 k ) s_{k} = (x^{k}_{2} - x^{k}_{1},y^{k}_{2} - y^{k}_{1}) sk=(x2k−x1k,y2k−y1k),预测点得到的宽高为 S ^ p k \hat{S}_{pk} S^pk,所以可以得到宽高的预测损失:
2.4 overall loss
在CenterNet中不归一化比例,直接使用原始像素坐标。用一个常数λ来衡量损失。
总的损失公式为:
L d e t = L k + λ s i z e L s i z e + λ o f f L o f f L_{det} = L_{k} + \lambda_{size}L_{size} + \lambda_{off}L_{off} Ldet=Lk+λsizeLsize+λoffLoff
其中λsize=0.1,λoff=1。
网络预测每个地点总共有C + 4个输出。所有输出共享一个公共的全卷积骨干网络。对于每个模态,最后的特征图分别通过一个3x3卷积,ReLU激活函数与一个1x1卷积,分别得到三个预测结果(heatmap,size,offset)。按我的理解,也就是接了三个head。

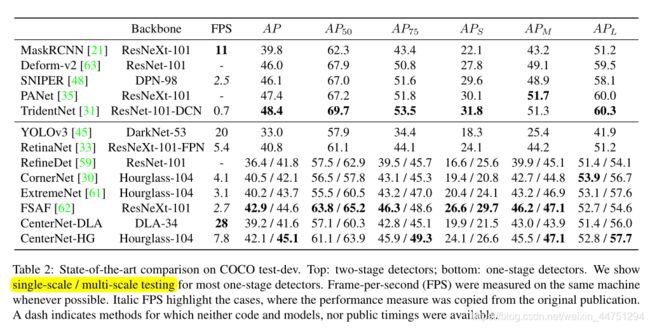
(对于目标检测主要看第一行,通过三个head分别获取heatmap,offset,size)
在backbone之后接了三个分支网络,分别用于预测heatmap(c个通道),size(2个通道),offset(2通道)。所有最后每个位置共有C+4个通道。如下图所示:

heatmap分支即keypoint prediction分支,heatmap有c个channel,对应c个类。最后挑选每个channel中peaks作为该类的center points。
size分支用于预测宽和高,offset分支用于弥补卷积操作的下采样导致离散误差,做回归用,这两个分支与类无关,所有类共享。
(图片参考:https://blog.csdn.net/yanghao201607030101/article/details/110202400)
3. Objects as Points
在推断的时候,首先独立地提取每个类别的heatmap中的峰值。如果一个点的值大于或等于其八邻域(周围最近的8个点)中的所有值则视为peak,最后保留值最大的100个peaks。
假设全部中心点的集合为: P ^ = ( x ^ i , y ^ i ) i = 1 n \hat{P} = {(\hat{x}_{i},\hat{y}_{i})}_{i=1}^{n} P^=(x^i,y^i)i=1n,其中设 P ^ c \hat{P}_{c} P^c为C类中心点的集合。每个关键点位置由一个整数坐标给出 ( x i , y i ) (x_{i},y_{i}) (xi,yi)。我们使用关键点值 Y ^ x i , y i , c \hat{Y}_{x_{i},y_{i},c} Y^xi,yi,c作为其检测置信度的度量,并在位置上产生一个边界框。
( x ^ i + δ x ^ i − w ^ i / 2 , y ^ i + δ y ^ i − h ^ i / 2 , x ^ i + δ x ^ i + w ^ i / 2 , y ^ i + δ y ^ i + h ^ i / 2 , ) (\hat{x}_{i} + \delta\hat{x}_{i} - \hat{w}_{i}/2,\hat{y}_{i} + \delta\hat{y}_{i} - \hat{h}_{i}/2,\\ \hat{x}_{i} + \delta\hat{x}_{i} + \hat{w}_{i}/2,\hat{y}_{i} + \delta\hat{y}_{i} +\hat{h}_{i}/2,) (x^i+δx^i−w^i/2,y^i+δy^i−h^i/2,x^i+δx^i+w^i/2,y^i+δy^i+h^i/2,)
具体的四点坐标如上所示,也就是center加上偏移offset,再通过计算长与宽得到最终的bounding box。其中 O ^ δ x ^ i , δ y ^ i = ( δ x ^ i , δ y ^ i ) \hat{O}_{\delta\hat{x}_{i}, \delta\hat{y}_{i}} = (\delta\hat{x}_{i}, \delta\hat{y}_{i}) O^δx^i,δy^i=(δx^i,δy^i)表示偏移预测量,而 S ^ δ x ^ i , δ y ^ i = ( δ w ^ i , δ h ^ i ) \hat{S}_{\delta\hat{x}_{i}, \delta\hat{y}_{i}} = (\delta\hat{w}_{i}, \delta\hat{h}_{i}) S^δx^i,δy^i=(δw^i,δh^i)表示长宽尺度预测。
所有输出直接从关键点估计产生,无需基于IoU的非最大值抑制(NMS)或其他后处理。峰值关键点提取是一种充分的NMS替代方案,可以使用3 × 3最大池操作在器件上高效实现。
4. Result
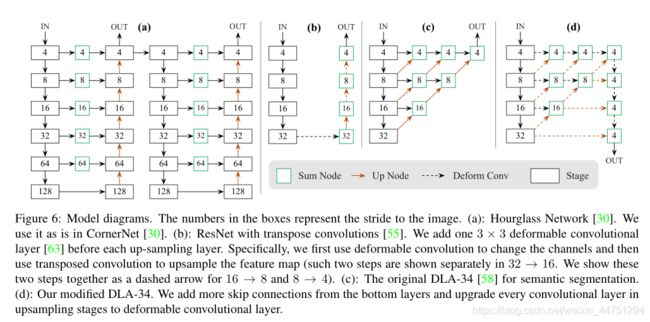
paper使用了四种不同的backbone进行实验:ResNet-18, ResNet-101, DLA-34 , 与 Hourglass-104 。其中对ResNets和DLA-34进行了更改,而 Hourglass-104 没有更改。结构如下:
四种backbone的实验结果: