RBF神经网络参数的参数优化(进化算法)+Matlab源码
@RBF神经网络参数的参数优化(进化算法)
1 RBF神经网络引入
1985年,Powell提出了多变量插值的径向基函数(RBF)方法。径向基函数是一个取值仅仅依赖于离原点距离的实值函数,也就是Φ(x)=Φ(‖x‖),或者还可以是到任意一点c的距离,c点称为中心点,也就是Φ(x,c)=Φ(‖x-c‖)。任意一个满足Φ(x)=Φ(‖x‖)特性的函数Φ都叫做径向基函数,标准的一般使用欧氏距离(也叫做欧式径向基函数),尽管其他距离函数也是可以的。其公式的一般表现如下,X表示样本点,Xi 是第i个rbf神经元的中心,σi为聚类宽度。
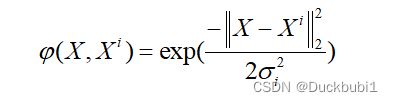
其三层结构如下图: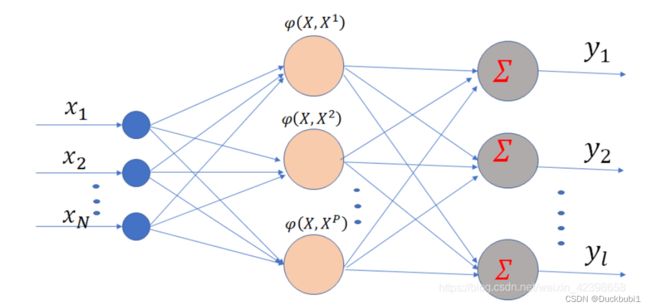
2 数据集
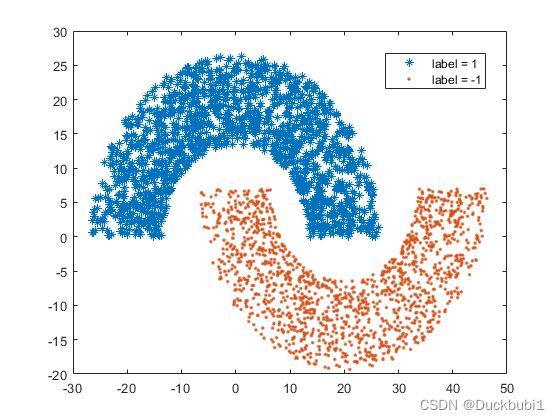
一个二维两分类的数据集dataset,数据为3000*3。前2列为特征,第三列为标签(取值1或-1)。在训练时使用前2500个作为训练集,后500个作为测试集。
2.1 三维展示:
2.2 二维展示:
3 RBF神经网络
1、 传统方法是使用k-means确定聚类中心和宽度。基于梯度方法更新权值。
2、不同的rbf中心个数设定会影响最终训练误差。此方法在初始化rbf个数、中心和宽度后,将不再改变
3、其函数实现如下,仅供参考(未经核实)
3.1 RBF实现 Matlab源码
clc;clear;close;
%%数据导入
d = load("data1.mat");
data = (d.data)';
dat=data(1:2500,1:2);
labels=data(1:2500,3);
%参数设置
inputNums=2;
outputNums=1;
hideNums= 10 %人为设定rbf个数
maxcount=1e4; %max_iter
samplenum = 2500; %training data
precision=0.001; %精度
alpha= 0.01;
%参数记录
error=zeros(1,maxcount);
errorp=zeros(1,samplenum);
w=rand(hideNums,outputNums);
%% k-means 确定rbf中心和宽度
[Idx,C]=kmeans(dat,hideNums);
dd=zeros(1,hideNums); %% RBF宽度
for i=1:hideNums
dmin=10000;
for j=1:hideNums
ddd=(C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2;
if(ddd0&&data(i,3)==1)||(net<=0&&data(i,3)==-1))
train_count=train_count+1;
end
end
%% 计算测试误差
% 隐含层输出矩阵
test=zeros(500,hideNums);
for i=2501:3000
for j=1:hideNums
test(i-2500,j)=exp( -( (data(i,1)-C(j,1))^2+(data(i,2)-C(j,2))^2 )/(2*dd(j)) );
end
end
test_count=0;
for i=2501:3000
net= 0.0;
for j=1:hideNums
net=net+test(i-2500,j)*w(j,1);
end
if((net>0&&data(i,3)==1)||(net<=0&&data(i,3)==-1))
test_count=test_count+1;
end
end
train_count;
train_error = 1-(train_count/2500)
test_count;
test_error = 1-(test_count/500)
3.2 结果统计
使用不同的隐藏层个数进行训练,记录其训练误差和测试误差,其结果如下表。

总结:不同的rbf神经元个数设置是会影响最终的误差,当hideNums=7时训练误差和测试误差均很小,当hideNums=10时,有100%的训练样本和测试样本准确率。
4 进化算法优化RBF参数
基于梯度下降的优化方法,其优化目标为训练误差或者测试误差等最小化,本质是一个优化问题。若将rbf的参数:中心,宽度和隐层到输出层的权值作为优化输入参数,其训练误差或是测试误差最小化作为优化目标。便可使用进化算法进行优化。其实现可以是:
4.1 main函数
此时设置rbf神经元个数为2。(即 hideNums = 2)
clear;clc;close;
load ('data1.mat');
d = data';
hideNums = 2;
iter_max = 1e4;
pop_num = 100;
best_fitness = zeros(iter_max,1);
[m,n] =size(d);
dim = n-1;
data_max = max(d(:,1:dim));
data_min = min(d(:,1:dim));
sigma_max = max(data_max-data_min);
W_max = 2*ones(1,hideNums);
W_min = -2*ones(1,hideNums);
x_max =[];
x_min =[];
% 一个rbf中心需要 dim+2 的参数 , 聚类中心维度dim ,宽度 1 ,权值矩阵 1
for j=1:hideNums
x_max = [x_max,data_max];
x_min = [x_min,data_min];
end
% 个体上1:hideNums*dim 为聚类中心参数 dim*hideNums+1:(dim+1)*hideNums 为聚类宽度,
% (dim+1)*hideNums+1:(dim+2)*hideNums 为隐层到输出层权值
x_max = [x_max,sigma_max*ones(1,hideNums),W_max];
x_min = [x_min,zeros(1,hideNums),W_min];
% initial
for i = 1:pop_num
x_pop(i,1:hideNums*(dim+2)) = rand(1,hideNums*(dim+2)).*(x_max-x_min)+x_min;
end
x_pop(:,hideNums*(dim+2)+1) = eluvate(x_pop,d,hideNums); %% 计算一次适应度
[~,index]=max(x_pop(1,:));
x_best = x_pop(index,1:hideNums*(dim+2));
best_fitness(1) = x_pop(index,hideNums*(dim+2)+1);
%iter
for iter = 2:iter_max
disp(['第',num2str(iter),'次迭代']);
x_pop = DE(x_pop,iter,iter_max,x_best,x_min,x_max,d,hideNums); %返回 pop_num*3
best_fitness(iter) = x_pop(1,hideNums*(dim+2)+1);
x_best = x_pop(1,1:hideNums*(dim+2));
end
plot(best_fitness);
title(['min最优值 ',num2str(best_fitness(end))]);
% xlabel(['best [x1,x2] = ',num2str(x_best)]);
ylabel("fitness");
x_best
best_fitness(iter_max);
4.2 DE实现函数
此处的DE算法使用自适应的控制参设置(F ,CR),该方法基于最大迭代次数非线性的递增或递减,变异使用新的策略。该方法来自于某篇国内论文[1],简单易实现。本文仅选择一种可行的方法实现验证,并不做过多评价。
function x_pop = DE(x_pop,iter,iter_max,x_best,x_min,x_max,d,hideNums)
% 设置
F = 1- iter/(iter+iter_max); % 缩放因子
CR = exp((iter-iter_max)/iter_max); % 交叉概率
x_temp = x_pop; %复制一份
[m,n]= size(x_pop); %%此处携带个体的适应度在最后一列
dim = n-1; %%此时dim 为算法求解的变量数
k = (iter_max-iter)/iter_max;
%% 1)变异
% 随机选取种群中两个不同的个体,将向量缩放后与待变异的个体进行向量合成 ,得到变异中间体
for i = 1:m
parent= choose_parent(i,m); %存放母本1,母本2,母本3的序号
x_pop(i,1:dim) = k * x_temp(i,1:dim) + (1-k)*x_best + F*(x_temp(parent(2),1:dim) - x_temp(parent(3),1:dim));
for j = 1:dim %%边界处理
if x_pop(i,j)>x_max(j) || x_pop(i,j) CR && j_rand ~= j
x_pop(i,j) = x_temp(i,j);
end
end
end
%% 3) 选择
% 1v1 选择。
x_pop(:,dim+1) = eluvate(x_pop(:,1:dim),d,hideNums);
t = x_pop(:,dim+1) > x_temp(:,dim+1);
x_pop = x_pop.*t + x_temp.*(1-t);
% for i =1:m
% if x_pop(i,n+1) > x_temp(i,n+1)
% x_temp(i,:) = x_pop(i,:);
% end
% end
%
% x_pop = x_temp;
end
function parent = choose_parent(i,m)
parent1 = i;
flag = 1;
while flag
parent2 = floor(rand*m);
parent3 = floor(rand*m);
if(parent2 ~= 0 && parent3 ~= 0)
if(parent1 ~= parent2 && parent1 ~= parent3)
if(parent2~= parent3)
flag = 0;
end
end
end
end
parent = [parent1,parent2,parent3];
end
4.3 函数评价
这一大类的进化算法,其实现难点就在于此,如何编写适应度评估函数!!
此时使用训练集预测准确率作为优化目标。
function fitness = eluvate(x_pop,d,hideNums)
[m,n] = size(x_pop);
dim = n/hideNums - 2;
data_num = size(d,1);
fitness = [];
for i =1:m
%列向量,每一行代表一个RBF宽度
rbf(i).sigma(1:hideNums) = x_pop(i,hideNums*(dim)+1:hideNums*(dim+1))';
%矩阵,每一行代表一RBF中心,
for k =1:hideNums
rbf(i).mu(k,1:dim) = x_pop(i,(k-1)*(dim)+1:k*(dim));
end
% 权重矩阵,权重矩阵第一列是偏置1
rbf(i).weight = [1,x_pop(i,hideNums*(dim+1)+1:hideNums*(dim+2))];
end
%给数据加x0 =1
train_data = d(1:2500,1:dim);
for i =1:m
for k = 1:hideNums
temp = (sum((train_data - rbf(i).mu(k,:)).^2,2));
rbf(i).z(:,k) = exp( -temp./(2*(rbf(i).sigma(k))^2));
end
% 加偏置 Z0 =1
rbf(i).z(:,1:hideNums+1) = [ones(2500,1),rbf(i).z];
end
for i = 1:m
rbf(i).out = rbf(i).z*(rbf(i).weight)';
rbf(i).predict = rbf(i).out;
rbf(i).predict(find(rbf(i).out < 0)) = -1;
rbf(i).predict(find(rbf(i).out >= 0)) = 1;
temp = rbf(i).predict.*d(1:2500,dim+1);
index = find(temp == 1);
rbf(i).count = length(index);
fitness = [fitness;rbf(i).count];
end
end
4.4 运行结果
运行完成后最优位置:
x_best = [21.2735176022600 7.18976834476119 28.0382989880820 -12.1554405903179 10.2756309083648 41.5810190156907 0.793344450152196 -1.62700237519134];
其适应度迭代情况如下图:
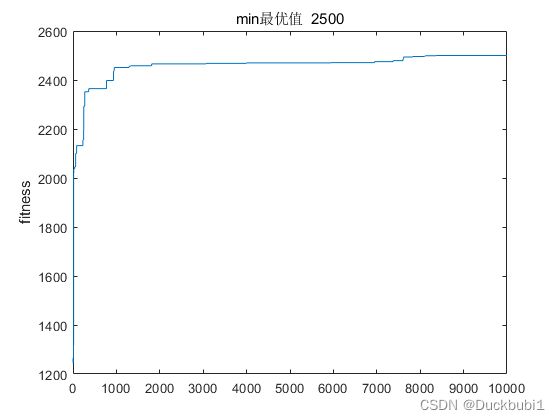
经过10000次的迭代训练样本的预测准确计数达到2500。即能实现完全预测(完全内插)。
4.5 测试误差
上述的优化目标为训练样本预测准确度,而训练网络的好坏还需计算测试误差。以下提供测试误差的计算实时函数,此函数需要在完成优化任务后的基础上进行,即得保留上次优化完成后的工作区变量。
[m,n] = size(x_best);
dim = n/hideNums - 2;
data_num = size(d,1);
fitness = [];
for i =1:m
%列向量,每一行代表一个RBF宽度
rbf(i).sigma(1:hideNums) = x_pop(i,hideNums*(dim)+1:hideNums*(dim+1))';
%矩阵,每一行代表一RBF中心,
for k =1:hideNums
rbf(i).mu(k,1:dim) = x_pop(i,(k-1)*(dim)+1:k*(dim));
end
% 权重矩阵,权重矩阵第一列是偏置1
rbf(i).weight = [1,x_pop(i,hideNums*(dim+1)+1:hideNums*(dim+2))];
end
test_data = d(2501:data_num,1:dim);
for i =1:m
for k = 1:hideNums
temp = (sum((test_data - rbf(i).mu(k,:)).^2,2));
rbf(i).z(:,k) = exp( -temp./(2*(rbf(i).sigma(k))^2));
end
% 加偏置 Z0 =1
rbf(i).z(:,1:hideNums+1) = [ones(500,1),rbf(i).z];
end
for i = 1:m
rbf(i).out = rbf(i).z*(rbf(i).weight)';
rbf(i).predict = rbf(i).out;
rbf(i).predict(find(rbf(i).out < 0)) = -1;
rbf(i).predict(find(rbf(i).out >= 0)) = 1;
temp = rbf(i).predict.*d(2501:data_num,dim+1);
index = find(temp == 1);
rbf(i).count = length(index);
fitness = [fitness;rbf(i).count];
end
fitness
运行结果为 fitness = 500,即测试样本预测准确!!
4.6 总结
此方法得到的RBF神经网络较为轻量,但优化耗时较长,仅为一种学习思路。并不提倡使用。
参考文献
[1] 张延莉. 函数优化问题求解的自适应差分进化算法[J]. 内蒙古师范大学学报(自然科学汉文版),2017,46(6):797-799.