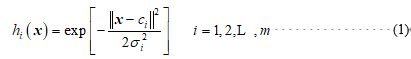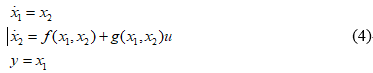rbf神经网络自适应控制matlab仿真_RBF神经网络及其在控制中的应用简介
目前，在控制领域内神经网络正在稳步地发展，这种发展的动力主要来自3个方面[1]：(1)处理越来越复杂的系统的需要；(2)实现越来越高的设计目标的需要；(3)在越来越不确定的情况下进行控制的需要。
在控制中，应用较多的网络是BP网络，但BP网络存在局部最优问题，并且训练速度慢，效率低。RBF网络在一定程度上克服了这些问题，因此它的研究与应用越来越得到重视。下面将简单介绍RBF神经网络的有关理论，以及其在控制中的应用。
1 RBF神经网络介绍
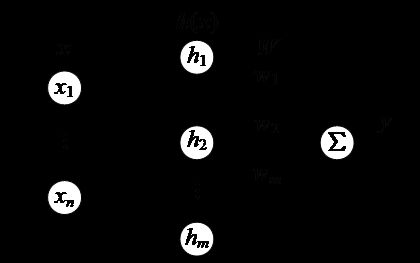
RBF神经网络(Radial Basis Function Neural Network)，即径向基神经网络，由Moody和 Darken在1988年提出，其结构如图1所示，是一种性能良好、具有单隐层的三层前向网络。输入层由信号源节点组成，第二层为隐含层，第三层为输出层。从输入空间到隐含层空间的变换是非线性的，而从隐含层空间到输match出层空间的变换是线性的，隐单元的变换函数是径向基函数，输出层神经元采用线性单元，RBF神经网络是一种局部分布的对中心径向对称衰减的非负非线性函数，已经证明，RBF网络是连续函数的最佳逼近，优于BP网络[2]。
径向基函数有许多种形式，其中最为常用的是高斯核函数：
其中，x是n维输入向量；ci是第i个基函数的中心；σi是平滑参数，决定了第i基函数中心点的宽度；m是感知单元的个数；
表示范数，通常取欧式范数。
输出表示为： 
上述算法表明，隐层节点中的作用函数对输人信号将在局部产生响应，即当输人信号越靠近基函数的中央范围时，隐层节点产生的输出就越大。
2 RBF神经网络
在控制中的应用
RBF神经网络在控制中的应用，可以按其隐含层与输出层连接权值的计算方式分为以下两类：
2.1 采用梯度下降法计算权值
采用梯度下降法计算神经网络权值的代表性研究工作如文献[3,4]。其基本思想为：首先根据控制方案设定误差指标，如控制误差指标、逼近误差指标E(t)，然后根据误差指标，采用梯度下降法，更新计算权值，具体调整方式见[2]。其控制方案主要有基于RBF神经网络的监督控制、基于RBF神经网络的模型参考自适应控制、基于RBF神经网络的自校正控制等三类。
图2为基于RBF神经网络的监督控制系统，RBF神经网络误差指标选取为，总控制输入与RBF网络输出的差值，即E(k)=1/2(un(k)-u(k))2，其控制思想为：初始阶段采用PD反馈控制，然后过渡到神经网络控制。在控制过程中，如出现较大的误差，则PD控制起主导作用，神经网络控制起调节作用。
图3为基于RBF神经网络的模型参考自适应控制，RBF神经网络误差指标选取为，理想系统输出与实际系统输出的差值，即E(k)=1/2(ym(k)-y(k))2，其控制思想为：将RBF神经网络作为控制器，依据参考模型的输出，实现系统的跟踪控制。
图4为基于RBF神经网络的自校正控制系统，该系统中，利用RBF神经网络逼近系统的未知函数或未知参数，然后用其逼近结果修正自校正控制器参数，RBF神经网络误差指标选取为逼近误差，即由RBF神经网络逼近系统模型得到的输出ym(k)与系统实际输出y(k)的差值。自校正控制可用于结构已知而参数未知但恒定的随机系统，也可用于结构已知而参数缓慢时变的随机系统。
采用梯度下降法计算神经网络权值，实现较为简单，但易陷人局部最优,且无法保证控制系统的稳定性和收敛性。
2.2 依据稳定性理论设计权值
依据稳定性理论设计权值，即通过分析系统的Lyapunov稳定性，设计权值，从而保证系统的稳定性和收敛性。
考虑如下二阶非线性系统，以自适应RBF控制器的设计为例，对该权值设计方式进行简要介绍。
其中，f为未知非线性函数；g为已知非线性函数；u∈Rn和y∈Rn分别为系统的控制输入和输出。
令
和
，(3)式可以改写为
设理想跟踪指令为yd，则误差为
设计
使多项式
的根都在左半复平面。
将RBF神经网络的输出代替式(3)中未知函数，可设计控制律为
其中，
为径向基函数，
为理想权值
的估计。
通过分析系统的稳定性，可以设计权值计算方式为
其中γ为正常数，
，矩阵P为对称正定的矩阵且满足如下Lyapunov方程：
其中，
则可通过设计RBF神经网络使逼近误差足够小，从而保证系统的稳定，证明见[1]。
在实际的控制系统设计中,为了保证网络的输人值处于高斯基函数的有效范围,应根据网络的输人值实际范围确定高斯基函数中心点坐标向量c值,为了保证高斯基函数的有效映射,需要将高斯基函数的宽度σ取适当的值。
依据稳定性理论设计的RBF神经网络，既可用于逼近未知参数或未知函数，又可直接作为控制器控制系统，进而又可以和鲁棒控制、滑模控制、反演控制等等理论相结合，进行控制器的设计。目前，已经产生了基于RBF神经网络的直接鲁棒自适应控制[5]、基于RBF神经网络的滑模控制[6]、基于RBF网络的动态面自适应控制[7]、以及基于RBF观测器的自适应控制[8]等等方法，为非线性控制问题的解决提供了新的思路。
3 总结
本文简要介绍了RBF神经网络以及其在控制中的应用，由于RBF神经网络独特的结构，可以大大加快学习速度并避免局部极小问题，可用于在线的辨识或控制，有着很大的发展潜力，可以进一步尝试应用于非线性系统的辨识与控制之中。
[1]刘金琨. RBF神经网络自适应控制MATLAB仿真[M]. 清华大学出版社, 2014.
[2] J.Park, I.W.Sandberg, Universal approximation using radial-basis-function networks[J], Neural Computation, 1991, 3(2): 246-257
[3] Noriega J R, Wang H (1998). A direct adaptive neural network control for unknown nonlinear systems and its application[J]. IEEE Trans Neural Netw 9(1) :27~34.
[4] Suykens, Johan. Artificial Neural Networks for Modeling and Control of Nonlinear Systems[M]// Artificial neural networks for modelling and control of non-linear systems. Kluwer Academic, 1995.
[5] Ge S S , Hang C C , Zhang T . A direct method for robust adaptive nonlinear control with guaranteed transient performance[J]. Systems & Control Letters, 1999, 37(5):275-284.
[6] Guo Yi, Jinkun LIU，Neural Network Based Adaptive Dynamic Surface Control for Flight Path Angle[C]，the 51th IEEE Conference on Decision and Control, December 10- 13，2012, 5374- 5379，Maui, Hawaii, USA, 2012.
[7] Sonfack L L , Kenné, Godpromesse, Fombu A M . An improved adaptive RBF neuro-sliding mode control strategy: Application to a static synchronous series compensator controlled system[J]. International Transactions on Electrical Energy Systems, 2019.
[8] Abdollahi F, Talebi H A, Patel R V (2006) A stable neural network based observer with application to flexible joint manipulators[J]. IEEE Trans Neural Netw 17(1):118~ 129.
end
关注我们
