《机器学习》学习笔记(四)——用Python代码实现单变量线性回归、多变量线性回归;数据评估之交叉验证法、留出法、自助法
机器学习(Machine Learning)是一门多学科交叉专业,涵盖概率论知识,统计学知识以及复杂算法知识,使用计算机作为工具并致力于真实实时的模拟人类学习方式, 并将现有内容进行知识结构划分来有效提高学习效率。本专栏将以学习笔记形式对《机器学习》的重点基础知识进行总结整理,欢迎大家一起学习交流!
专栏链接:《机器学习》学习笔记
目录
一、单变量线性回归
提出问题
分析问题
解决方案
模型评价
二、多变量线性回归
1:基于LinearRegression的实现
2:基于成本函数和梯度下降的实现
三、数据评估之交叉验证法、留出法、自助法
1:SVM分类器
2:K近邻分类器
一、单变量线性回归
提出问题
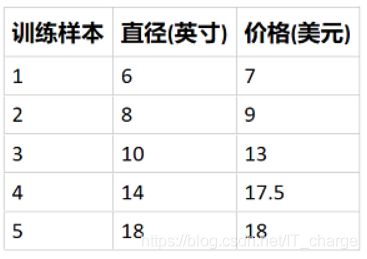
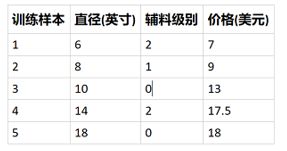
假设某披萨店的披萨价格和披萨直径之间有下列数据关系:
根据上面的训练数据,我们能否推断(预测)出某个直径的披萨可能的售价呢?例如,12英寸的披萨可能售卖多少钱?
分析问题
把直径看成自变量(以后也称特征值),价格看成因变量,可以先通过作图看出二者的关系:
import numpy as np
import matplotlib.pyplot as plt
def initPlot():
plt.figure() #先准备好一块画布
plt.title('Pizza Price vs Diameter') #表名字
plt.xlabel('Diameter') #横坐标名字
plt.ylabel('Price') #纵坐标名字
plt.axis([0, 25, 0, 25]) # 设置x轴和y轴的值域均为0~25
plt.grid(True) #表内有栅格
return plt
plt = initPlot() #画图
xTrain = np.array([6,8,10,14,18])
yTrain = np.array([7,9,13,17.5,18])
plt.plot(xTrain, yTrain, 'k.') #k是黑色,.是以点作为图上显示
plt.show(); #将图显示出来
可以看到:
- 价格随着直径的变化,大致呈现线性变化;
- 如果根据现有的训练数据能够拟合出一条直线,使之与这些训练数据的各点都比较接近,那么根据该直线,就可以计算出在任意直径披萨的价格。
解决方案
采用Python scikit-learn库中提供的sklearn.linear_model.LinearRegression对象来进行线性拟合
- 思路
拟合出来的直线可以表示为:ℎ()=00+11=0+11hθ(x)=θ0x0+θ1x1=θ0+θ1x1- 0x0 表示Intercept Term,一般设置为1即可
- 1x1 表示影响计算结果的的第一个因素(或称特征,在本例中就是直径)。在单变量线性回归中,只有1x1
- 0θ0表示截距,1θ1表示斜率。这两个参数都是需要通过拟合求出来的
- ℎ()hθ(x)称为判别函数(Hypothesis Function)或判别式,也就是线性拟合的模型结果函数
- 步骤
- 准备训练数据
xTrain = np.array([6,8,10,14,18])[:, np.newaxis]
yTrain = np.array([7,9,13,17.5,18])
LinearRegression支持单变量和多变量回归。对于多变量回归,xTrain显然是矩阵形式。因此,即使只有一个变量,LinearRegression也要求输入的特征值以矩阵形式(列向量)存在。
在使用LinearRegression时,不需要显式设置Intercept Item;它会自动扩展该列 - 创建模型对象
model = LinearRegression() - 执行拟合
hypothesis = model.fit(xTrain, yTrain)
判别函数(hypothesis)对象中包含了大量的属性和方法,可用于针对该模型的后续操作 - 获取判别函数的参数(截距和斜率)
print("theta0=", hypothesis.intercept_)
print("theta1=", hypothesis.coef_) - 预测新的数据
model.predict([[12]])
model.predict([[0],[10],[14],[25]])
将待预测的数据放置在一个矩阵(或列向量)中,可以批量预测多个数据
- 准备训练数据
- 结果
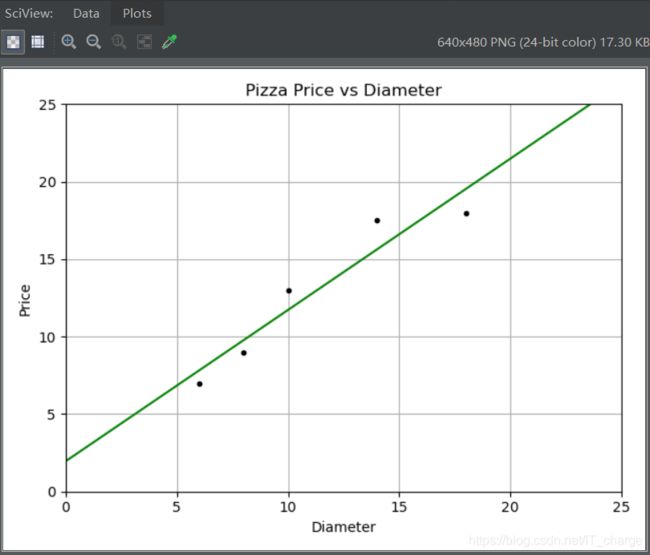
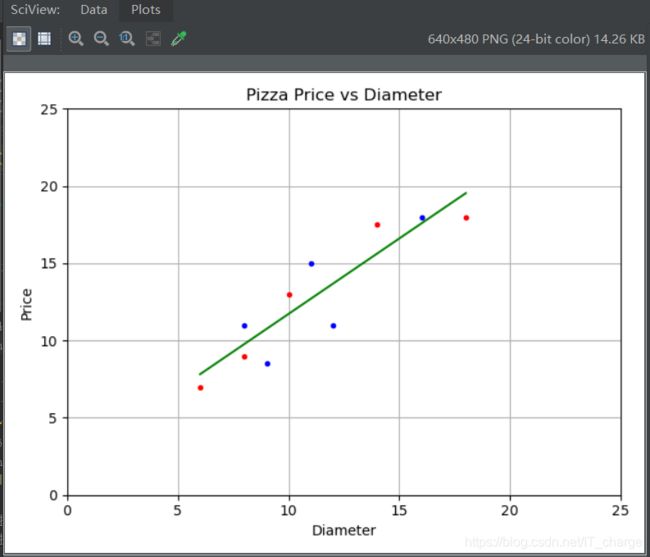
根据判别函数,绘制拟合直线,并同时显示训练数据点。
拟合的直线较好的穿过训练数据,根据新拟合的直线,可以方便的求出各个直径下对应的价格(预测结果)。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
xTrain = np.array([6, 8, 10, 14, 18])[:, np.newaxis] # 应以矩阵形式表达(对于单变量,矩阵就是列向量形式)
yTrain = np.array([7, 9, 13, 17.5, 18]) # 为方便理解,也转换成列向量
model = LinearRegression() # 创建模型对象
hypothesis = model.fit(xTrain, yTrain) # 根据训练数据拟合出直线(以得到假设函数)
print("theta0=", hypothesis.intercept_) # 截距
print("theta1=", hypothesis.coef_) # 斜率
print("预测直径12的披萨价格:", model.predict([[12]])) # 预测直径为12的披萨价格
xNew = np.array([0, 10, 14, 25])[:, np.newaxis] # 也可以批量预测多个直径,注意要以列向量形式表达
yNew = model.predict(xNew)
print("预测新数据:", xNew)
print("预测结果:", yNew)
def initPlot():
plt.figure()
plt.title('Pizza Price vs Diameter')
plt.xlabel('Diameter')
plt.ylabel('Price')
plt.axis([0, 25, 0, 25])
plt.grid(True)
return plt
plt = initPlot()
plt.plot(xTrain, yTrain, 'k.')
plt.plot(xNew, yNew, 'g-') # 画出通过这些点的连续直线
plt.show()
模型评价
拟合出来的判别函数效果如何:对训练数据的贴合度如何?对新数据的预测准确度如何?
先给出下列定义:
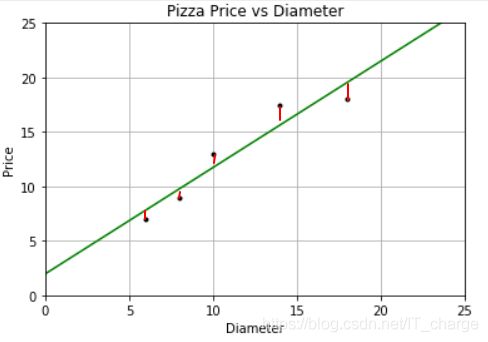
- 残差(residuals):判别函数计算结果与实际结果之间的差异,如下图中的红色线段部分。一般是计算残差平方和
- R方(r-squared):又称确定系数(coefficient of determination)。在通过训练数据得出了判别函数后,对于新的数据,如何评估该假设函数的表现呢?可以使用与训练数据不同的另一组数据(称为检验/测试数据)来进行评估。R方就是用来进行评估的一种计算方法。在Pyhton的scikit-learn中,是这样定义R方的(针对给定的测试数据):
=∑=1(()−⎯⎯⎯)2SStot=∑i=1m(y(i)−y¯)2
=∑=1[()−ℎ(())]2SSres=∑i=1m[y(i)−hθ(x(i))]2
2=1−R2=1−SSresSStot- m:测试数据集中的数据组数
- ()y(i):测试数据集中第i组数据的y值(实际价格)
- ⎯⎯⎯y¯:测试数据集中y的平均值
- ℎ(())hθ(x(i)):将()x(i)代入到判别函数计算的结果,也就是根据模型算出的y值(计算价格)
- SStot:针对测试数据计算出来偏差平方和
- SSres:针对测试数据计算出来的残差平方和
- 一般来说,R方越大(不会超过1),说明模型效果越好。如果R方较小或为负,说明效果很差
- 在Python中如何对单变量线性回归模型的效果进行评估
- 手动计算
假设hpyTrain代表针对训练数据的预测y值,hpyTest代表针对测试数据的预测y值- 训练数据残差平方和:
ssResTrain = sum((hpyTrain - yTrain) ** 2) - 测试数据残差平方和:
ssResTest = sum((hpyTest - yTest) ** 2) - 测试数据偏差平方和:
ssTotTest = sum((yTest - np.mean(yTest)) ** 2) - R方:
Rsquare = 1 - ssResTest / ssTotTest
- 训练数据残差平方和:
- LinearRegression对象提供的方法
- 训练数据残差平方和:
model._residues - R方:
model.score(xTest, yTest)
- 训练数据残差平方和:
- 手动计算
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
xTrain = np.array([6,8,10,14,18])[:,np.newaxis] # 训练数据(直径)
yTrain = np.array([7,9,13,17.5,18]) # 训练数据(价格)
xTest = np.array([8,9,11,16,12])[:,np.newaxis] # 测试数据(直径)
yTest = np.array([11,8.5,15,18,11]) # 测试数据(价格)
model = LinearRegression()
hypothesis = model.fit(xTrain, yTrain)
hpyTrain = model.predict(xTrain)
hpyTest = model.predict(xTest) # 针对测试数据进行预测
ssResTrain = sum((hpyTrain - yTrain)**2) # 手动计算训练数据集残差
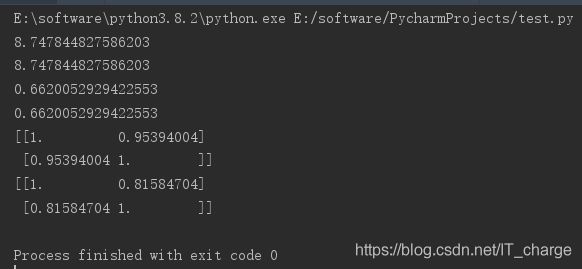
print(ssResTrain) # 8.7478
print(model._residues) # Python计算的训练数据集残差
ssResTest = sum((hpyTest - yTest)**2) # 手动计算测试数据集残差
ssTotTest = sum((yTest - np.mean(yTest))**2) # 手动计算测试数据集y值偏差平方和
Rsquare = 1 - ssResTest / ssTotTest # 手动计算R方
print(Rsquare) # 0.662
print(model.score(xTest, yTest)) # Python计算的训练数据集的R方
# corrcoef函数是在各行元素之间计算相关性,所以x和y都应是行向量
print(np.corrcoef(xTrain.T, yTrain.T)) # 计算训练数据的相关性:0.954
print(np.corrcoef(xTest.T, yTest.T)) # 计算测试数据的相关性:0.816
def initPlot():
plt.figure()
plt.title('Pizza Price vs Diameter')
plt.xlabel('Diameter')
plt.ylabel('Price')
plt.axis([0, 25, 0, 25])
plt.grid(True)
return plt
plt = initPlot()
plt.plot(xTrain, yTrain, 'r.') # 训练点数据(红色)
plt.plot(xTest, yTest, 'b.') # 测试点数据(蓝色)
plt.plot(xTrain, hpyTrain, 'g-') # 假设函数直线(绿色)
plt.show()二、多变量线性回归
在之前的但变量线性回归实验中,披萨价格仅与直径有关,按照这一假设,其预测的结果并不令人满意(R方=0.662)。本章再引入一个新的影响因素:披萨辅料级别(此处已经把辅料级别调整成数值,以便能够进行数值计算)。训练数据如下:
另外提供测试数据如下:
如何使用线性回归训练数据,并且判断是否有助于提升预测效果呢?
1:基于LinearRegression的实现
与单变量线性回归类似,但要注意训练数据此时是(是训练数据条数,是自变量个数),在本例中,是5x2的矩阵:xTrain = np.array([[6,2],[8,1],[10,0],[14,2],[18,0]])
针对测试数据的预测结果,其R方约为0.77,已经强于单变量线性回归的预测结果
''' 使用LinearRegression进行多元线性回归 '''
import numpy as np
from sklearn.linear_model import LinearRegression
xTrain = np.array([[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]]) # 无需手动添加Intercept Item项
yTrain = np.array([7, 9, 13, 17.5, 18])
xTest= np.array([[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]])
yTest = np.array([11, 8.5, 15, 18, 11])
model = LinearRegression()
model.fit(xTrain, yTrain)
hpyTest = model.predict(xTest)
print("假设函数参数:", model.intercept_, model.coef_)
print("测试数据预测结果与实际结果差异:", hpyTest - yTest)
print("测试数据R方:", model.score(xTest, yTest))
2:基于成本函数和梯度下降的实现
对于一个自变量1的情形,与的关系用一条直线就可以拟合 (假设有一定线性相关性)。对于有两个自变量1,2x1,x2的情形, 与的关系就需要用一个平面来拟合。如果有更多的自变量,虽然 无法在三维空间中展现,但仍然可以用数学的方式来描述它们之间 的关系。
''' 批量梯度下降法实现多元线性回归 '''
import numpy as np
import matplotlib.pyplot as plt
import bgd_resolver
def costFn(theta, X, y): # 成本函数
temp = X.dot(theta) - y
return (temp.T.dot(temp)) / (2 * len(X))
def gradientFn(theta, X, y): # 根据成本函数,分别对x0,x1...xn求导数(梯度)
return (X.T).dot(X.dot(theta) - y) / len(X)
xTrainData = np.array([[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]])
yTrain = np.array([7, 9, 13, 17.5, 18])
xTrain = np.c_[xTrainData, np.ones(len(xTrainData))]
np.random.seed(0)
init_theta = np.random.randn(xTrain.shape[1])
theta = bgd_resolver.batch_gradient_descent(costFn, gradientFn, init_theta, xTrain, yTrain)
print("theta值", theta)
xTestData = np.array([[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]])
yTest = np.array([11, 8.5, 15, 18, 11])
xTest = np.c_[xTestData, np.ones(len(xTestData))]
print("测试数据预测值与真实值的差异:", xTest.dot(theta) - yTest)
rsquare = bgd_resolver.batch_gradient_descent_rsquare(theta, xTest, yTest)
print("测试数据R方:", rsquare)三、数据评估之交叉验证法、留出法、自助法
1:SVM分类器
from sklearn.model_selection import train_test_split,cross_val_score,cross_validate # 交叉验证所需的函数(train_test_split对数据集和训练集做数据上的分割;cross_val_score做交叉验证;cross_validate也是做交叉验证)
from sklearn.model_selection import KFold,LeaveOneOut,LeavePOut,ShuffleSplit # 交叉验证所需的子集划分方法(KFold做k折交叉验证;LeaveOneOut留一法;LeavePOut留P个;ShuffleSplit打乱)
from sklearn.model_selection import StratifiedKFold,StratifiedShuffleSplit # 分层分割(StratifiedKFold使得分得的和原数据集中的比例及数目一致)
from sklearn.model_selection import GroupKFold,LeaveOneGroupOut,LeavePGroupsOut,GroupShuffleSplit # 分组分割
from sklearn.model_selection import TimeSeriesSplit # 时间序列分割
from sklearn import datasets # 自带数据集
from sklearn import svm # SVM算法(分类算法)
from sklearn import preprocessing # 预处理模块
from sklearn.metrics import recall_score # 模型度量(查全率、查准率)
import numpy as np
iris = datasets.load_iris() # 加载数据集(系统自带的“花”数据集)
print('样本集大小:',iris.data.shape,iris.target.shape) #data是属性,targrt是标签,shape看大小
# ===================================数据集划分,训练模型==========================
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.4, random_state=0) #40%作为测试集 # 交叉验证划分训练集和测试集.test_size为测试集所占的比例
print('训练集大小:',X_train.shape,y_train.shape) # 训练集样本大小
print('测试集大小:',X_test.shape,y_test.shape) # 测试集样本大小
clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train) # 使用训练集训练模型
print('准确率:',clf.score(X_test, y_test)) # 计算测试集的度量值(准确率)
# 如果涉及到归一化,则在测试集上也要使用训练集模型提取的归一化函数。
scaler = preprocessing.StandardScaler().fit(X_train) # 通过训练集获得归一化函数模型。(也就是先减几,再除以几的函数)。在训练集和测试集上都使用这个归一化函数
X_train_transformed = scaler.transform(X_train)
clf = svm.SVC(kernel='linear', C=1).fit(X_train_transformed, y_train) # 使用训练集训练模型
X_test_transformed = scaler.transform(X_test)
print('归一化后的准确率:', clf.score(X_test_transformed, y_test)) # 计算测试集的度量值(准确度)
# ===================================直接调用交叉验证评估模型==========================
clf = svm.SVC(kernel='linear', C=1)
scores = cross_val_score(clf, iris.data, iris.target, cv=5) #cv为迭代次数。
print('交叉验证评估分数:', scores) # 打印输出每次迭代的度量值(准确度)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2)) # 获取置信区间。(也就是均值和方差)
# ===================================多种度量结果======================================
scoring = ['precision_macro', 'recall_macro'] # precision_macro为精度(查准率),recall_macro为召回率(查全率)
scores = cross_validate(clf, iris.data, iris.target, scoring=scoring, cv=5, return_train_score=True)
sorted(scores.keys()) #排序
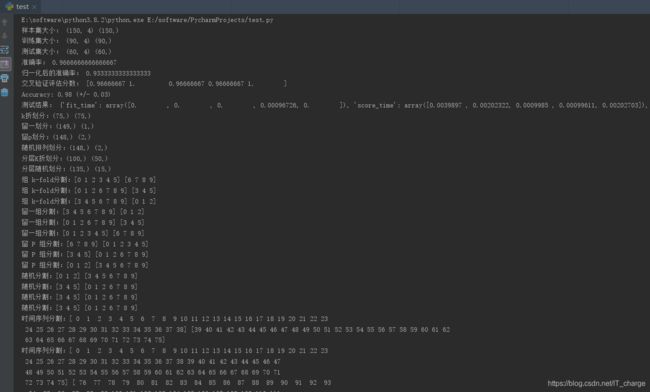
print('测试结果:',scores) # scores类型为字典。包含训练得分,拟合次数, score-times (得分次数)
# ==================================K折交叉验证、留一交叉验证、留p交叉验证、随机排列交叉验证==========================================
# k折划分子集
kf = KFold(n_splits=2)
for train, test in kf.split(iris.data):
print("k折划分:%s %s" % (train.shape, test.shape))
break
# 留一划分子集
loo = LeaveOneOut()
for train, test in loo.split(iris.data):
print("留一划分:%s %s" % (train.shape, test.shape))
break
# 留p划分子集
lpo = LeavePOut(p=2)
for train, test in lpo.split(iris.data):
print("留p划分:%s %s" % (train.shape, test.shape))
break
# 随机排列划分子集
ss = ShuffleSplit(n_splits=3, test_size=0.25,random_state=0)
for train_index, test_index in ss.split(iris.data):
print("随机排列划分:%s %s" % (train.shape, test.shape))
break
# ==================================分层K折交叉验证、分层随机交叉验证==========================================
skf = StratifiedKFold(n_splits=3) #各个类别的比例大致和完整数据集中相同
for train, test in skf.split(iris.data, iris.target):
print("分层K折划分:%s %s" % (train.shape, test.shape))
break
skf = StratifiedShuffleSplit(n_splits=3) # 划分中每个类的比例和完整数据集中的相同
for train, test in skf.split(iris.data, iris.target):
print("分层随机划分:%s %s" % (train.shape, test.shape))
break
# ==================================组 k-fold交叉验证、留一组交叉验证、留 P 组交叉验证、Group Shuffle Split==========================================
X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]
groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]
# k折分组
gkf = GroupKFold(n_splits=3) # 训练集和测试集属于不同的组
for train, test in gkf.split(X, y, groups=groups):
print("组 k-fold分割:%s %s" % (train, test))
# 留一分组
logo = LeaveOneGroupOut()
for train, test in logo.split(X, y, groups=groups):
print("留一组分割:%s %s" % (train, test))
# 留p分组
lpgo = LeavePGroupsOut(n_groups=2)
for train, test in lpgo.split(X, y, groups=groups):
print("留 P 组分割:%s %s" % (train, test))
# 随机分组
gss = GroupShuffleSplit(n_splits=4, test_size=0.5, random_state=0)
for train, test in gss.split(X, y, groups=groups):
print("随机分割:%s %s" % (train, test))
# ==================================时间序列分割==========================================
tscv = TimeSeriesSplit(n_splits=3)
TimeSeriesSplit(max_train_size=None, n_splits=3)
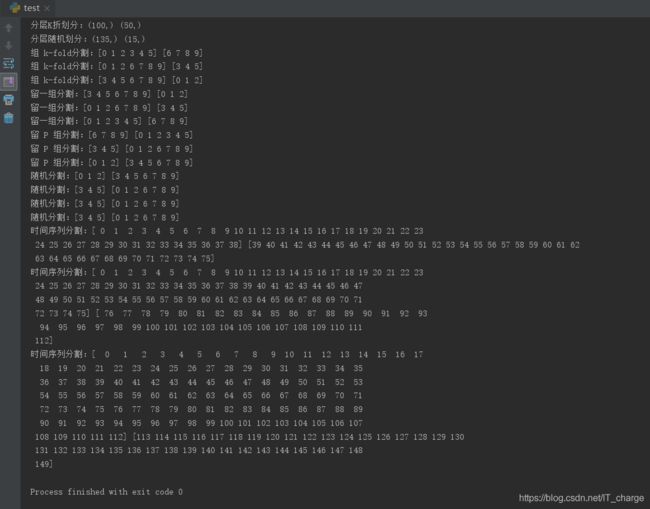
for train, test in tscv.split(iris.data):
print("时间序列分割:%s %s" % (train, test))2:K近邻分类器
from sklearn import datasets #自带数据集
from sklearn.model_selection import train_test_split,cross_val_score #划分数据 交叉验证
from sklearn.neighbors import KNeighborsClassifier #一个简单的模型,只有K一个参数,类似K-means
import matplotlib.pyplot as plt
iris = datasets.load_iris() #加载sklearn自带的数据集
X = iris.data #这是数据
y = iris.target #这是每个数据所对应的标签
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=1/3,random_state=3) #这里划分数据以1/3的来划分 训练集训练结果 测试集测试结果
k_range = range(1,31)
cv_scores = [] #用来放每个模型的结果值
for n in k_range:
knn = KNeighborsClassifier(n) #knn模型,这里一个超参数可以做预测,当多个超参数时需要使用另一种方法GridSearchCV
scores = cross_val_score(knn,train_X,train_y,cv=10,scoring='accuracy') #accuracy准确率 #cv:选择每次测试折数 accuracy:评价指标是准确度,可以省略使用默认值,具体使用参考下面。
cv_scores.append(scores.mean())
plt.plot(k_range,cv_scores)
plt.xlabel('K')
plt.ylabel('Accuracy') #通过图像选择最好的参数
plt.show()
best_knn = KNeighborsClassifier(n_neighbors=3) # 选择最优的K=3传入模型
best_knn.fit(train_X,train_y) #训练模型
print(best_knn.score(test_X,test_y)) #看看评分
欢迎留言,一起学习交流~~~
感谢阅读