披萨价格和直径-机器学习实验笔记(单变量线性回归)
目录
- 1 单变量回归原理(不涉及数学推导)
-
- 1.1 基本原理介绍
- 1.2 sklearn库相关方法和参数介绍
- 2 披萨价格和直径案例
-
- 2.1 案例代码
1 单变量回归原理(不涉及数学推导)
1.1 基本原理介绍
回归分析(Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法 ,是一种预测性的建模技术,线性回归,简单而言,就是将输入项分别乘以一些常量,再将结果加起来得到输出。线性回归包括一元线性回归和多元线性回归。
线型回归分析中,如果仅有一个自变量与一个因变量,且其关系大致上可用一条直线表示,则称之为单变量线性回归。
如果发现因变量Y和自变量X之间存在高度的相关,可以确定一条直线的方程,使得所有的数据点尽可能接近这条拟合的直线。单变量线性回归的模型可以用以下方程表示:
Y = a + bx
- Y 因变量
- a 截距
- b 相关系数
- x 自变量
1.2 sklearn库相关方法和参数介绍
使用sklearn库建立单变量线性回归模型
sklearn线性回归方法及默认参数:
sklearn.linear_model.LinearRegression(
*,
fit_intercept=True,
normalize='deprecated',
copy_X=True,
n_jobs=None,
positive=False)
模型部分方法
fit(X, y[, sample_weight]) #拟合模型
coef_ #获取截距和相关系数
get_params([deep]) #获得模型参数
predict(X) #使用模型进行预测
score(X, y[, sample_weight]) #返回预测的准确率
set_params(**params) #设置模型参数
model._residues #训练数据残差平方和
sklearn.linear_model.LinearRegression详细介绍
2 披萨价格和直径案例
2.1 案例代码
import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt
import pandas as pd
df=pd.read_csv('./pizza_train.csv')
x_train=df['d'].values.reshape(-1,1)
y_train=df['price'].values.reshape(-1,1)
#--------------根据数据创建单变量线性回归模型-------------#
reg =linear_model.LinearRegression()
reg.fit(x_train,y_train)
k = reg.coef_ # 获取斜w1,w2,w3....wn
b = reg.intercept_ # 获取截距
print(k,b)
y0=k*x_train+b
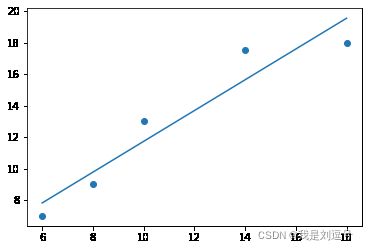
plt.figure()
plt.scatter(x_train,y_train)
plt.plot(x_train,y0)
plt.show()
#--------------预测披萨价格-------------#
test=pd.read_csv('./pizza_test.csv')
x_test=test['d'].values.reshape(-1,1)
y_test=test['price'].values.reshape(-1,1)
y_predict=reg.predict(x_test)
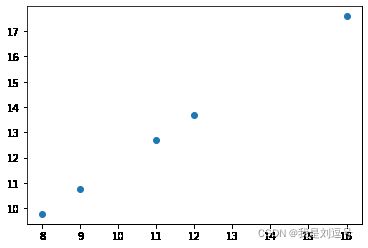
plt.figure()
plt.scatter(x_test,y_predict)
plt.show()
#--------------评价模型准确率-------------#
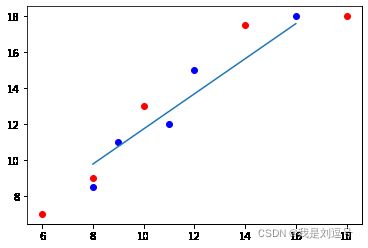
plt.scatter(x_train,y_train,color='red')
plt.scatter(x_test,y_test,color='blue')
plt.plot(x_test,y_predict)
plt.show()
residues=reg._residues
r=reg.score(x_test,y_test)
print(residues,r)