小波神经网络的基本原理,小波神经网络算法原理

1、什么是“小波神经网络”？能干什么用呀

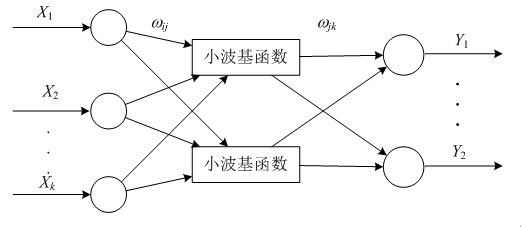
小波神经网络（Wavelet Neural Network， WNN）是在小波分析研究获得突破的基础上提出的一种人工神经网络。它是基于小波分析理论以及小波变换所构造的一种分层的、多分辨率的新型人工神经网络模型。

 即用非线性小波基取代了通常的非线性Sigmoid 函数，其信号表述是通过将所选取的小波基进行线性叠加来表现的。它避免了BP 神经网络结构设计的盲目性和局部最优等非线性优化问题，大大简化了训练，具有较强的函数学习能力和推广能力及广阔的应用前景。

“小波神经网络”的应用：

1、在影像处理方面，可以用于影像压缩、分类、识别与诊断，去污等。在医学成像方面的减少B超、CT、核磁共振成像的时间，提高解析度等。

2、在信号分析中的应用也十分广泛。它可以用于边界的处理与滤波、时频分析、信噪分离与提取弱信号、求分形指数、信号的识别与诊断以及多尺度边缘侦测等。

3、在工程技术等方面的应用。包括电脑视觉、电脑图形学、曲线设计、湍流、远端宇宙的研究与生物医学方面。

扩展资料：

小波神经网络这方面的早期工作大约开始于1992 年，主要研究者是Zhang Q、Harold H S 和焦李成等。其中，焦李成在其代表作《神经网络的应用与实现》中从理论上对小波神经网络进行了较为详细的论述。近年来，人们在小波神经网络的理论和应用方面都开展了不少研究工作。

小波神经网络具有以下特点：首先，小波基元及整个网络结构的确定有可靠的理论根据，可避免BP 神经网络等结构设计上的盲目性；其次，网络权系数线性分布和学习目标函数的凸性，使网络训练过程从根本上避免了局部最优等非线性优化问题；第三，有较强的函数学习能力和推广能力。

谷歌人工智能写作项目：小发猫

2、小波神经网络的优势是什么？谢谢

小波神经网络相比于前向的神经网络,它有明显的优点:首先小波神经网络的基元和整个结构是依据小波分析理论确定的,可以避免BP神经网络等结构设计上的盲目性;其次小波神经网络有更强的学习能力,精度更高小波变换神经网络。总的而言，对同样的学习任务,小波神经网络结构更简单,收敛速度更快，精度更高。

3、人工神经网络的发展趋势

人工神经网络特有的非线性适应性信息处理能力，克服了传统人工智能方法对于直觉，如模式、语音识别、非结构化信息处理方面的缺陷，使之在神经专家系统、模式识别、智能控制、组合优化、预测等领域得到成功应用。人工神经网络与其它传统方法相结合，将推动人工智能和信息处理技术不断发展。近年来，人工神经网络正向模拟人类认知的道路上更加深入发展，与模糊系统、遗传算法、进化机制等结合，形成计算智能，成为人工智能的一个重要方向，将在实际应用中得到发展。将信息几何应用于人工神经网络的研究，为人工神经网络的理论研究开辟了新的途径。神经计算机的研究发展很快，已有产品进入市场。光电结合的神经计算机为人工神经网络的发展提供了良好条件。
神经网络在很多领域已得到了很好的应用，但其需要研究的方面还很多。其中，具有分布存储、并行处理、自学习、自组织以及非线性映射等优点的神经网络与其他技术的结合以及由此而来的混合方法和混合系统，已经成为一大研究热点。由于其他方法也有它们各自的优点，所以将神经网络与其他方法相结合，取长补短，继而可以获得更好的应用效果。目前这方面工作有神经网络与模糊逻辑、专家系统、遗传算法、小波分析、混沌、粗集理论、分形理论、证据理论和灰色系统等的融合。
下面主要就神经网络与小波分析、混沌、粗集理论、分形理论的融合进行分析。
与小波分析的结合
1981年，法国地质学家Morlet在寻求地质数据时，通过对Fourier变换与加窗Fourier变换的异同、特点及函数构造进行创造性的研究，首次提出了小波分析的概念，建立了以他的名字命名的Morlet小波。1986年以来由于YMeyer、S.Mallat及IDaubechies等的奠基工作，小波分析迅速发展成为一门新兴学科。Meyer所著的小波与算子，Daubechies所著的小波十讲是小波研究领域最权威的著作。
小波变换是对Fourier分析方法的突破。它不但在时域和频域同时具有良好的局部化性质，而且对低频信号在频域和对高频信号在时域里都有很好的分辨率，从而可以聚集到对象的任意细节。小波分析相当于一个数学显微镜，具有放大、缩小和平移功能，通过检查不同放大倍数下的变化来研究信号的动态特性。因此，小波分析已成为地球物理、信号处理、图像处理、理论物理等诸多领域的强有力工具。
小波神经网络将小波变换良好的时频局域化特性和神经网络的自学习功能相结合，因而具有较强的逼近能力和容错能力。在结合方法上，可以将小波函数作为基函数构造神经网络形成小波网络，或者小波变换作为前馈神经网络的输入前置处理工具，即以小波变换的多分辨率特性对过程状态信号进行处理，实现信噪分离，并提取出对加工误差影响最大的状态特性，作为神经网络的输入。
小波神经网络在电机故障诊断、高压电网故障信号处理与保护研究、轴承等机械故障诊断以及许多方面都有应用，将小波神经网络用于感应伺服电机的智能控制，使该系统具有良好的跟踪控制性能，以及好的鲁棒性，利用小波包神经网络进行心血管疾病的智能诊断，小波层进行时频域的自适应特征提取，前向神经网络用来进行分类，正确分类率达到94%。
小波神经网络虽然应用于很多方面，但仍存在一些不足。从提取精度和小波变换实时性的要求出发，有必要根据实际情况构造一些适应应用需求的特殊小波基，以便在应用中取得更好的效果。另外，在应用中的实时性要求，也需要结合DSP的发展，开发专门的处理芯片，从而满足这方面的要求。
混沌神经网络
混沌第一个定义是上世纪70年代才被Li-Yorke第一次提出的。由于它具有广泛的应用价值，自它出现以来就受到各方面的普遍关注。混沌是一种确定的系统中出现的无规则的运动，混沌是存在于非线性系统中的一种较为普遍的现象，混沌运动具有遍历性、随机性等特点，能在一定的范围内按其自身规律不重复地遍历所有状态。混沌理论所决定的是非线性动力学混沌，目的是揭示貌似随机的现象背后可能隐藏的简单规律，以求发现一大类复杂问题普遍遵循的共同规律。
1990年Kaihara、T.Takabe和M.Toyoda等人根据生物神经元的混沌特性首次提出混沌神经网络模型，将混沌学引入神经网络中，使得人工神经网络具有混沌行为，更加接近实际的人脑神经网络，因而混沌神经网络被认为是可实现其真实世界计算的智能信息处理系统之一，成为神经网络的主要研究方向之一。
与常规的离散型Hopfield神经网络相比较，混沌神经网络具有更丰富的非线性动力学特性，主要表现如下：在神经网络中引入混沌动力学行为；混沌神经网络的同步特性；混沌神经网络的吸引子。
当神经网络实际应用中，网络输入发生较大变异时，应用网络的固有容错能力往往感到不足，经常会发生失忆现象。混沌神经网络动态记忆属于确定性动力学运动，记忆发生在混沌吸引子的轨迹上，通过不断地运动(回忆过程)一一联想到记忆模式，特别对于那些状态空间分布的较接近或者发生部分重叠的记忆模式，混沌神经网络总能通过动态联想记忆加以重现和辨识，而不发生混淆，这是混沌神经网络所特有的性能，它将大大改善Hopfield神经网络的记忆能力。混沌吸引子的吸引域存在，形成了混沌神经网络固有容错功能。这将对复杂的模式识别、图像处理等工程应用发挥重要作用。
混沌神经网络受到关注的另一个原因是混沌存在于生物体真实神经元及神经网络中，并且起到一定的作用，动物学的电生理实验已证实了这一点。
混沌神经网络由于其复杂的动力学特性，在动态联想记忆、系统优化、信息处理、人工智能等领域受到人们极大的关注。针对混沌神经网络具有联想记忆功能，但其搜索过程不稳定，提出了一种控制方法可以对混沌神经网络中的混沌现象进行控制。研究了混沌神经网络在组合优化问题中的应用。
为了更好的应用混沌神经网络的动力学特性，并对其存在的混沌现象进行有效的控制，仍需要对混沌神经网络的结构进行进一步的改进和调整，以及混沌神经网络算法的进一步研究。
基于粗集理论
粗糙集(Rough Sets)理论是1982年由波兰华沙理工大学教授Z.Pawlak首先提出，它是一个分析数据的数学理论，研究不完整数据、不精确知识的表达、学习、归纳等方法。粗糙集理论是一种新的处理模糊和不确定性知识的数学工具，其主要思想就是在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则。目前，粗糙集理论已被成功应用于机器学习、决策分析、过程控制、模式识别与数据挖掘等领域。
粗集和神经网络的共同点是都能在自然环境下很好的工作，但是，粗集理论方法模拟人类的抽象逻辑思维，而神经网络方法模拟形象直觉思维，因而二者又具有不同特点。粗集理论方法以各种更接近人们对事物的描述方式的定性、定量或者混合性信息为输入，输入空间与输出空间的映射关系是通过简单的决策表简化得到的，它考虑知识表达中不同属性的重要性确定哪些知识是冗余的，哪些知识是有用的，神经网络则是利用非线性映射的思想和并行处理的方法，用神经网络本身结构表达输入与输出关联知识的隐函数编码。
在粗集理论方法和神经网络方法处理信息中，两者存在很大的两个区别：其一是神经网络处理信息一般不能将输入信息空间维数简化，当输入信息空间维数较大时，网络不仅结构复杂，而且训练时间也很长；而粗集方法却能通过发现数据间的关系，不仅可以去掉冗余输入信息，而且可以简化输入信息的表达空间维数。其二是粗集方法在实际问题的处理中对噪声较敏感，因而用无噪声的训练样本学习推理的结果在有噪声的环境中应用效果不佳。而神经网络方法有较好的抑制噪声干扰的能力。
因此将两者结合起来，用粗集方法先对信息进行预处理，即把粗集网络作为前置系统，再根据粗集方法预处理后的信息结构，构成神经网络信息处理系统。通过二者的结合，不但可减少信息表达的属性数量，减小神经网络构成系统的复杂性，而且具有较强的容错及抗干扰能力，为处理不确定、不完整信息提供了一条强有力的途径。
目前粗集与神经网络的结合已应用于语音识别、专家系统、数据挖掘、故障诊断等领域，将神经网络和粗集用于声源位置的自动识别，将神经网络和粗集用于专家系统的知识获取中，取得比传统专家系统更好的效果，其中粗集进行不确定和不精确数据的处理，神经网络进行分类工作。
虽然粗集与神经网络的结合已应用于许多领域的研究，为使这一方法发挥更大的作用还需考虑如下问题：模拟人类抽象逻辑思维的粗集理论方法和模拟形象直觉思维的神经网络方法更加有效的结合；二者集成的软件和硬件平台的开发，提高其实用性。
与分形理论的结合
自从美国哈佛大学数学系教授Benoit B. Mandelbrot于20世纪70年代中期引入分形这一概念，分形几何学(Fractal geometry)已经发展成为科学的方法论--分形理论，且被誉为开创了20世纪数学重要阶段。现已被广泛应用于自然科学和社会科学的几乎所有领域，成为现今国际上许多学科的前沿研究课题之一。
由于在许多学科中的迅速发展，分形已成为一门描述自然界中许多不规则事物的规律性的学科。它已被广泛应用在生物学、地球地理学、天文学、计算机图形学等各个领域。
用分形理论来解释自然界中那些不规则、不稳定和具有高度复杂结构的现象，可以收到显著的效果，而将神经网络与分形理论相结合，充分利用神经网络非线性映射、计算能力、自适应等优点，可以取得更好的效果。
分形神经网络的应用领域有图像识别、图像编码、图像压缩，以及机械设备系统的故障诊断等。分形图像压缩/解压缩方法有着高压缩率和低遗失率的优点，但运算能力不强，由于神经网络具有并行运算的特点，将神经网络用于分形图像压缩/解压缩中，提高了原有方法的运算能力。将神经网络与分形相结合用于果实形状的识别，首先利用分形得到几种水果轮廓数据的不规则性，然后利用3层神经网络对这些数据进行辨识，继而对其不规则性进行评价。
分形神经网络已取得了许多应用，但仍有些问题值得进一步研究：分形维数的物理意义；分形的计算机仿真和实际应用研究。随着研究的不断深入，分形神经网络必将得到不断的完善，并取得更好的应用效果。?

4、小波变换在高光谱影像处理中的应用

小波分析在遥感图像处理中的应用起步比较晚，主要是对图像进行二维小波变换和重构，常用于一般遥感图像压缩、图像去噪、图像融合、图像纹理特征和边缘特征分析、图像插值处理、多卫星数据融合、图像数据分类等方面。

由于小波变换具有多分辨率分析的特点，在时、频两域都具有表征信号局部特征的能力，对高光谱波谱维进行小波分解能够同时保留信号高频与低频信息，精细地描述光谱的波峰和波谷等曲线特性，自动消除数据中的异常值，大大减少了特征光谱维数（Kaewpi－jit，2003），因而有利于高光谱后续处理。如基于小波变换，可提取信号在不同分级上的小波分量特征值，可利用特征值匹配方法实现了高光谱影像的分类（李新双等，2006）。结合小波变换的特点和非监督正交子空间迭代分解的方法，也可利用基于光谱维的小波低频系数特征或高频特征系数，进行混合像元投影迭代分解或亚像素目标识别（吴波等，2005；路威等，2005a）。孙桂玲等（2006）对典型地物的高光谱数据采用小波变换的分析方法，根据小波分解后的高频信息中包含重要信息的特点，提出了一种能够比较精确的提取出地物光谱各个吸收带的中心波长的光谱特征提取方法。

相对来说，小波变换在高光谱影像处理中主要用于高光谱影像数据的压缩（王晋等，2006）、融合、去噪（路威等，2005b；吴传庆等，2005）、影像分类、小波神经网络分类、影像亚像素目标识别、特征提取等。小波变换在高光谱影像数据的光谱分析和光谱特征提取中的应用还比较少，这方面应用以对各个像元或参考目标的高光谱数据进行小波变换为基础，主要用于光谱特征提取、目标识别与分类和高光谱遥感影像亚像素目标识别。

5、神经网络以及小波分析法在汽车发动机故障检修中有什么应用？

汽车是我们生活中常用的将交通工具，那么神经网络和小波分析法在汽车发动机故障检修中有什么应用呢？大家请看我接下来详细地讲解。

一，小波分析在故障检修中的应用

小波包分解与故障特征提取。缸盖表面的振动信号由一系列瞬态响应信号组成，分别代表气缸的振动源响应信号:1为气缸的燃烧激励响应;2是排气阀打开时的节流阀冲击。气门间隙异常时,振动信号的能量大于目前冲击力作用时,振动信号的主要组件目前离冲击力稳定的振动信号和噪声,信号能量相对较小。因此，可以利用每个频带的能量变化来提取故障特征，通过小波包分解系数{4]得到频带的能量。

二，神经网络在故障检修中的作用

神经网络与故障识别的基本原理。人工神经网络以其大规模并行处理、分布式存储、自组织、自适应和自学习的能力，以及适合于处理不准确或模糊的信息而备受关注5]。其中，最成熟的是BP神经网络。值，直到输出接近理想输出信号6。因此，BP神经网络可以以任意精度逼近任意有限维函数，适用于模式识别。现在对每个工况信号取5个样本，按照⒉部分所述步骤对35组样本信号进行编程，提取样本信号的能量特征向量。

三，小波分析法和神经网络应用总结

为了实现柴油机气门机构的非解体故障诊断，本文将对测量的气缸盖振动信号进行小波阈值降噪预处理。然后根据信号的频率特性，对信号进行时频分析后进行小波包分解。所构造的能量特征向量准确地反映了气门间隙状态下缸盖振动信号能量的变化。实验表明，利用能量特征向量，BP神经网络能更准确地完成从振动信号空间到气门间隙状态空间的非线性映射，能更好地满足柴油机状态检测和故障诊断的要求。

6、论文求助：数字信号识别（基于小波变换，基于人工神经网络） 30

数字信号识别（基于小波变换，基于人工神经网络）,什么要求哦，咋办.

7、用小波分析法除去音频信号的噪声

小波变换及其应用是八十年代后期发展起来的应用数学分支，被称为“Fourier分析方法的突破性进展[1]”。 1986年Meyer Y构造了一个真正的小波基，十多年间小波分析及其应用得到了迅速发展，原则上传统的傅里叶分析可用小波分析方法取代[2],它能对几乎所有的常见函数空间给出通过小波展开系数的简单刻划，也能用小波展开系数描述函数的局部光滑性质，特别是在信号分析中，由于它的局部分析性能优越，因而在数据压缩与边缘检测等方面它比现有的手段更为有效[3-8]。 小波变换在图像压缩中的应用因它的高压缩比和好的恢复图像质量而引起了广泛的注意，且出现了各种基于小波变换的图像压缩方案。
小波变换自1992年Bos M等[9]首先应用于流动注射信号的处理，至今虽才8年时间，但由于小波变换其优良的分析特性而迅速渗透至分析化学信号处理的各个领域。本文介绍了小波变换的基本原理及其在分析化学中的应用情况。
1 基本原理
设f(t)为色谱信号，其小波变换在L2(R)中可表示为：

其中a, b∈R,a≠0,参数a称为尺度因子b为时移因子，而(Wf)(b, a)称为小波变换系数，y(t)为基本小波。在实际分析化学信号检测中其时间是有限长度，f(t)通常以离散数据来表达，所以要采用Mallat离散算法进行数值计算，可用下式表示：
fj+1=θj + f j
其中:N为分解起始尺度;M为分解次数；fj和qj可由下式求得：

此处:Φj, m为尺度函数;Ψj, m 为小波函数;系数Cmj ,dmj可由下式表达：

hk-2m , gk-2m取决于小波母函数的选取。
用图表示小波分解过程如下：

图中fN 、fN-1....fN-m和θN-1、θN-2....θN-m分别称为在尺度N上的低频分量和高频分量。上述分解过程的逆过程即是信号的重构过程。
2 分析化学中的应用
根据小波变换基本原理及其优良的多分辩分析特性，本文将小波变换在分析化学信号处理中的应用划归为以下三个方面：
2.1 信号的滤波
小波滤波方法目前在分析化学中应用主要是小波平滑和小波去噪两种方法。小波平滑是将某一信号先经小波分解，将在时间域上的单一信号分解为一系列不同尺度上的小波系数(也称不同频率上的信号), 然后选定某一截断尺度，使高于此尺度的小波系数全部为零，再重构信号，这样就完成了一个低通小波滤波器的设计；而小波去噪，则是在小波分解基础上选定一阈值，对所有尺度空间的小波系数进行比较，使小于此阈值的小波系数为零，然后重构信号[10]。
邵利民[11]等首次将小波变换应用于高效液相色谱信号的滤波，他们应用了Haar小波母函数，由三次小波分解后所得的低频部分重构色谱信号，结果成功地去除了噪声，明显地提高了色谱信号的信噪比，而色谱峰位保持一致，此法提高了色谱的最低检测量和色谱峰的计算精度。董雁适[12]等提出了基于色谱信号的小波自适应滤波算法，使滤波与噪声的频带分布，强度及信噪在频带上的交迭程度基本无关，具有较强的鲁棒性。
在光谱信号滤噪中的应用，主要为红外光谱和紫外光谱信号滤噪方面的应用，如Bjorn K A[13]等将小波变换用于红外光谱信号的去噪，运用6种不同的小波滤噪方法(SURE，VISU，HYBRID，MINMAX，MAD和WP)对加噪后红外光谱图进行了去噪,针对加噪与不加噪的谱图，对Fourier变换、移动平均滤波与小波滤波方法作了性能比较研究，结果认为Fourier变换、移动平均滤波等标准滤波方法在信噪比很低时滤噪性能与小波滤波方法差不多，但对于高信噪比的信号用小波滤噪方法(特别是HYBRID和VISU)则更有效 。闵顺耕[14]等对近红外漫反射光谱进行了小波变换滤波。顾文良[15]等对示波计时电信号进行了滤噪处理。王立世[16]等对电泳信号也做了小波平滑和去噪,都取得了满意的效果。邹小勇[17]等利用小波的时频特性去除了阶跃伏安信号中的噪音，并提出了样条小波多重滤波分析方法，即将过滤后的高频噪音信号当成原始信号进行滤波处理，使之对有用信号进行补偿。鲍伦军等[18]将样条小波和傅里叶变换联用技术应用于高噪音信号的处理。另外，程翼宇[19]等将紫外光谱信号的滤噪和主成分回归法进行了有机的结合，提出了小波基主成分回归(PCRW)方法，改善了主成分回归算法。
2.1 信号小波压缩
信号经小波分解之后，噪音信号会在高频部分出现，而对于有用的信号分量大部分在低频部分出现，据此可以将高频部分小波系数中低于某一阈值的系数去除，而对其余系数重新编码，只保留编码后的小波系数，这样可大大减少数据贮存量，达到信号压缩的目的。
在近代分析化学中分析仪器的自动化水平在不断提高，分析仪器所提供的数据量越来越大。寻找一种不丢失有效信息的数据压缩方法，节省数据的贮存量，或降低与分析化学信息处理有关的一些算法的处理量，已成为人们关心的问题。Chau F T等[20]用快速小波变换对模拟和实验所得的紫外可见光谱数据进行了压缩，讨论了不同阶数的Daubechies小波基、不同的分解次数及不同的阈值对压缩结果的影响。Barclay V J和Bonner R F[10]对实验光谱数据作了压缩，压缩率可达1/2~1/10,并指出在数据平滑和滤噪的同时，也能进行数据的压缩是小波有别与其他滤波方法的一大特点。王洪等[21]用Daubechies二阶正交小波基对聚乙烯红外光谱进行了成功的压缩，数据可压缩至原来的1/5以下。邵学广等[22]对一维核磁共振谱数据作了小波变换压缩，分别对常用的Haar、Daubechies以及Symmlet小波基作了比较，其结果表明准对称的Symmlet小波基对数据的复原效果最佳，而且在压缩到64倍时，均方差仍然较小。章文军等[23]提出了常用小波变换数据压缩的三种方法，将紧支集小波和正交三次B-样条小波压缩4-苯乙基邻苯二甲酸酐的红外光谱数据进行了对比，计算表明正交三次B-样条小波变换方法效果较好，而在全部保留模糊信号及只保留锐化信号中数值较大的系数时，压缩比大而重建光谱数据与原始光谱数据间的均方差较小。邵学广等[24]将小波数据压缩与窗口因子分析相结合，在很大程度上克服了用窗口因子分析直接处理原始信号时人工寻找最佳窗口的困难，在压缩比高达8:1的情况下，原始信号中的有用信息几乎没有丢失，窗口因子分析的解析时间大为缩短。Bos M等[25]用Daubechies小波对红外光谱数据进行压缩，压缩后的数据作为人工神经网络算法的输入接点，从而提高了人工神经网络的训练速度，预测的效果也比直接用光谱数据训练的要好。
2.3 小波多尺度分析
在多尺度分析方面的应用主要是对化学电信号进行小波分解，使原来单一的时域信号分解为系列不同频率尺度下的信号，然后对这些信号进行分析研究。
小波在色谱信号处理方面的应用，主要是对重叠色谱峰的解析。邵学广[26-27]等对苯、甲苯、乙苯三元体系色谱重叠峰信号小波变换后的某些频率段进行放大，然后重构色谱信号，使重叠色谱峰得到了分离，定量分析结果得到了良好的线性关系。此后邵学广[28]等利用了谱峰提取法对植物激素重叠色谱峰作了定量计算，此法表明，利用小波变换从重叠色谱信号中提取的各组分的峰高与浓度之间仍然具有良好的线性关系。
重叠伏安峰的分辨是电分析化学中一个长期存在的难题。当溶液中存在两种或更多的电活性物质，而这些物质的氧化(或还原)电位又很靠近时，就会不可避免地出现重叠峰的现象，而给进一步的定性、定量分析带来了很大困难。因此，人们做了较多的工作去解决这一难题。数学方法是目前处理重叠峰的重要手段，如Fourier变换去卷积以及曲线拟合。曲线拟合通常用来获得“定量”的信息，但这种方法有较多的人为因素，重叠峰包含的峰的个数，相对强度都是靠假设得来，因而可能引入严重的误差；去卷积方法则是一种频域分析手段，但该方法需先找出一个函数来描述伏安峰，然后再根据这个函数来确定去卷积函数，因此，去卷积函数的确定是比较麻烦的，尤其是对不可逆电极过程，无法找到一个合适的函数表达式，而且该方法还需经正、反Fourier变换，比较繁琐费时, 而小波分析的出现成了电分析化学家关注的热点。
陈洁等[29]用DOG小波函数处理差分脉冲实验数据，通过选择合适的伸缩因子，成功地延长了用DPV法测定Cu2+的线性范围。郑建斌等[30-31]将小波变换用于示波计时电位信号的处理，在有用信息提取、重叠峰分辨等方面进行了系统的研究。王洪等[32]将小波边缘检测的思想用于电位滴定终点的确定，找到了一种判断终点准确的终点判断方法。郑小萍等[33]将样条小波变换技术用于分辨重叠的伏安峰，以选定的分辨因子作用于样条小波滤波器，构造了一个小波峰分辨器，用它来直接处理重叠的伏安峰，取得了较好的分离效果，被处理重叠峰可达到完全基线分离，且峰位置和峰面积的相对误差均较小。
对于红外光谱图，目前也是通过对红外谱图进行小波分解，以提高红外谱图的分辩率。陈洁[34]等对辐射合成的丙烯酰胺、丙烯酸钠共聚物水凝胶的红外光谱信号经小波处理后，使其特征吸收带较好地得到分离，成功地提高了红外光谱图的分辨率。谢启桃[35]等对不同晶型聚丙烯红外光谱图作了小波变换，也得到了可用以区分聚丙烯a、b两晶型的红外光谱图。
3 展望
小波变换由于其优良的局部分析能力，使其在分析化学信号的滤噪、数据压缩和谱峰的分离方面得到了很好的应用。本人通过对小波变换在化学中应用的探索，认为对于分析化学中各种电信号的平滑、滤波还有待作更深入的研究，以设计出更为合理有效的小波滤波器，以消除由于平滑而导至的尖锐信号的峰高及峰面积的变化或由于去噪而带来的尖锐信号附近的不应有的小峰的出现；对于重叠峰的分离及其定量计算，还应该探讨如色谱峰基线的确定方法以及待分离频率段的倍乘系数的确定方法；另外对于色谱峰的保留指数定性问题，由于不同化合物在某一确定的分析条件下有可能会出现保留值相同的情况，这将使在未知样中加标准的峰高叠加法定性或外部标准物对照定性变得困难，我们是否可能对色谱峰进行小波分解，然后在不同的尺度上对其进行考察，以寻求色谱峰的小波定性方法，这可能是个可以进一步研究的问题。
小波变换将在分析化学领域得到更加广泛的应用，特别对于分析化学中的多元定量分析法，如多元线性回归法(MLR)，主成分回归法(PCR)，偏最小二乘法(PLS)等方法及人工神经网络(ANN)将会同小波变换进行有机的结合，以消除各种噪声干扰对定量分析的影响；或对相关数据进行压缩以减少待分析数据的冗余，提高分析精度和大大减少计算量提高分析速度。小波变换将会成为分析化学中定量和定性分析的一种非常重要的工具。

8、神经网络研究现状

光谱分析因其能够灵敏、高精度、无破坏、快速地检测物质的化学成分和相对含量而广泛应用于分析化学、生物化学与分子生物学、农业、医学等领域。目前，光谱分析技术日趋成熟，引入光谱分析理论的高光谱遥感技术应用日益广泛，尤其是在农业领域，可以有效地获取农田信息、判断作物长势、估测作物产量、提取病害信息。光谱分析技术虽然具有很强的物质波谱“透视力”，但在分析 “同谱异物” 和 “异物同谱”等方面需要与现代分析手段相结合，如小波变换、卡尔曼滤波、人工神经网络（Artificial Neural Net－work，ANN）、遗传算法（Genetic Algorithm，GA）等。

在光谱分析领域，ANN多用于物质生化组分的定量分析（陈振宁等，2001；印春生等，2000），在光度分析中也有较多应用，如，于洪梅等（2002）利用ANN分析铬和锆的混合吸收光谱，并结合分光度法对二者进行测定。ANN在非线性校准与光谱数据处理等方面也有应用（Blank，1993；方利民等；2008）。而在模式识别中ANN应用最为广泛，如，Eiceman et al.（2006）利用遗传算法（是ANN的一种）对混合小波系数进行分类识别。

目前，自组织特征映射（Self－organizing Feature Maps，SOFM）神经网络在高光谱影像的模式识别方面，国内外还较少有研究与应用，而结合遥感波谱维光谱分析技术的应用研究就更少。SOFM常用于遥感图像处理方面，如，Moshou et al.（2005）利用SOFM神经网络进行数据融合，使分类误差减小到1％；Doucette et al.（2001）根据SOFM设计的SORM算法，从分类后的高分辨率影像中提取道路；Toivanen et al.（2003）利用SOFM神经网络从多光谱影像中提取边缘，并指出该方法可应用于大数据量影像边缘的提取；Moshou et al.（2006）根据5137个叶片的光谱数据，利用SOFM神经网络识别小麦早期黄锈病，准确率高达99％。然而，SOFM不需要输入模式期望值（在某些分类问题中，样本的先验类别是很难获取的），其区别于BP（Back Propagation）等其他神经网络模型最重要的特点是能够自动寻找样本的内在规律和本质属性，这大大地拓宽了SOFM在模式识别和分类方面的应用。

基于以上几点，本章从光谱分析的角度对高光谱遥感影像进行分析识别和信息提取，给出了在不同光谱模型下，高光谱数据的不同分解，之后利用SOFM对具有较高光谱重叠度的这些分解进行分类识别，结合光谱分析对采样点进行类别辨识，并通过对小麦条锈病的病情严重度信息提取，提出了高光谱影像波谱维光谱分析的新途径。