【交通流预测】《T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction》论文详解
《T-GCN》文章目录
- 文章总结
- Abstract
- 一、Introduction
- 二、Related work
- 三、METHODOLOGY
-
- 1. Problem Definition
- 2. Overview
- 3. Methodology
- 3. Temporal Graph Convolutional Network
- 四、Experiments
-
- 1. 数据集
- 2. 评价指标
- 3. 模型参数选择
- 3. Experiment Results
- 五、 Conclusion
点击论文+代码程序下载链接:https://github.com/sttCharon/Traffic_Prediction_Paper_code
文章总结
-
- 现存问题:
① 空间性:传统模型考虑了交通条件的动态变化,而忽略了空间依赖性,使得交通状况的变化不受路网的限制,不能准确预测交通数据的状态。
② 数据:卷积神经网络通常用于欧几里德数据,如图像、规则网格等。此类模型无法在具有复杂拓扑结构的城市道路网的背景下工作,因此本质上无法描述空间相关性。 -
- 文章贡献点:
① 提出新的模型框架: T-GCN模型集成了GCN和GRU。GCN用于捕捉道路网络的拓扑结构,以建模空间相关性。GRU用于捕捉道路上交通数据的动态变化,以建模时间依赖性。T-GCN模型也可应用于其他时空预测任务。 T-GCN模型不仅可以实现短期预测,而且可以用于长期交通预测任务。与所有的基线方法相比,预测误差降低了约1.5%-57.8%。
Abstract
准确、实时的交通预测在智能交通系统中占有重要地位,对城市交通规划、交通管理和交通控制具有重要意义。然而,由于城市道路网络拓扑结构的约束和随时间动态变化的规律,交通预测一直被认为是一个开放的科学问题。为了同时捕获空间和时间依赖关系,我们提出了一种新的基于神经网络的交通量预测方法,即时间图卷积网络(T-GCN)模型,该模型与图卷积网络(GCN)和选通递归单元(GRU)相结合。具体而言,GCN用于学习复杂拓扑结构以获取空间相关性,而选通递归单元用于学习交通数据的动态变化以获取时间相关性。然后,将T-GCN模型应用于基于城市道路网的交通预测。实验表明,我们的T-GCN模型可以从交通数据中获得时空相关性,并且预测性能优于现实世界交通数据集的最新基线。
一、Introduction
预测背景:随着智能交通系统的发展,交通预测越来越受到人们的重视。它是先进交通管理系统的关键部分,是实现交通规划、交通管理和交通控制的重要组成部分。交通预测是分析城市道路包括流量、速度和密度,挖掘交通模式,预测道路交通趋势等交通状况的过程。交通预测不仅可以为交通管理者提前感知交通拥堵和限制车辆提供科学依据,还可以为城市出行者选择合适的出行路线和提高出行效率提供安全保障。然而,由于其复杂的空间和时间依赖性,交通预测一直是一项具有挑战性的任务:
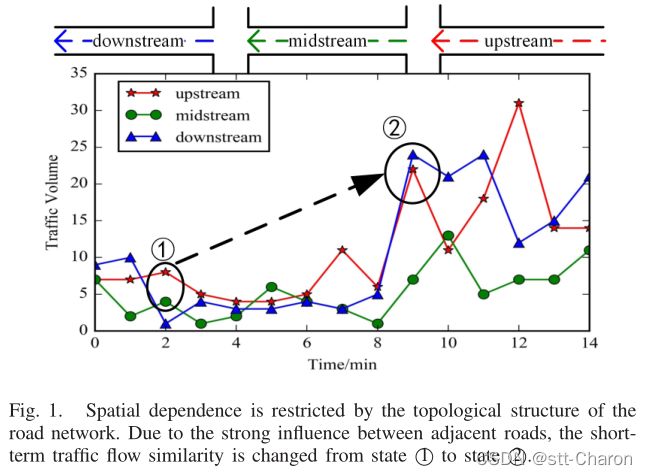
- 空间依赖性:交通量的变化主要取决于城市道路网的拓扑结构。上游道路的交通状态通过传递效应影响下游道路的交通状态,下游道路的交通状态通过反馈效应影响上游的交通状态。如图1所示,由于相邻道路之间的强烈影响,短期相似性从状态①(上游道路类似于中游道路)更改为状态②(上游道路类似于下游道路)。
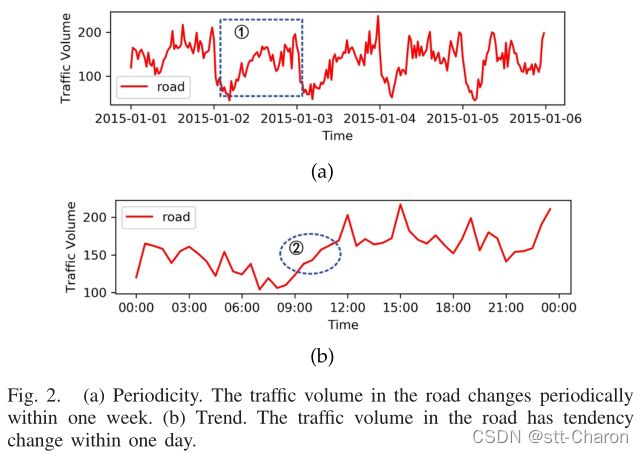
- 时间依赖性:交通量随时间动态变化,主要表现为周期性和趋势性。如图2(a)所示,道路交通量在一周内呈周期性变化。如图2(b)所示,一天的交通量随时间变化;例如,当前交通量受前一时刻甚至更长时间的交通状况的影响。
现有模型:自回归综合移动平均(ARIMA)模型、Kalman滤波模型、支持向量回归机模型、k-最近邻模型、贝叶斯模型]和部分神经网络模型。上述方法考虑了交通条件的动态变化,而忽略了空间依赖性,使得交通状况的变化不受路网的限制,不能准确预测交通数据的状态。为了更好地描述空间特征,一些研究引入了用于空间建模的卷积神经网络;然而,卷积神经网络通常用于欧几里德数据,如图像、规则网格等。此类模型无法在具有复杂拓扑结构的城市道路网的背景下工作,因此本质上无法描述空间相关性。
贡献:
- T-GCN模型集成了图卷积网络和选通递归单元。图卷积网络用于捕捉道路网络的拓扑结构,以建模空间相关性。选通递归单元用于捕捉道路上交通数据的动态变化,以建模时间依赖性。T-GCN模型也可应用于其他时空预测任务。
- T-GCN模型的预测结果表明,在不同的预测视界下,T-GCN模型处于稳定状态,这表明T-GCN模型不仅可以实现短期预测,而且可以用于长期交通预测任务。
- 我们使用两个真实的交通数据集来评估我们的方法。结果表明,与所有的基线方法相比,我们的方法将预测误差降低了约1.5%-57.8%,并证明了T-GCN模型在交通量预测方面的优越性。
二、Related work
模型分类: 现有的交通预测方法可分为两类:模型驱动方法和数据驱动方法。首先,模型驱动方法主要解释交通流量、速度和密度之间的暂态和稳态关系。这种方法需要基于先验知识全面和详细的系统建模。代表性方法包括排队论模型(queuing theory model)、元胞传输模型(cell transmission model)、“交通速度”模型、微观基本图模型(microscopic fundamental diagram model)等。
模型驱动方法的缺陷:现实中,交通数据受多种因素的影响,很难获得准确的交通模型。现有模型不能准确描述复杂现实环境中交通数据的变化。此外,这些模型的构建需要显著的计算能力,并且容易受到交通干扰和采样点间距等的影响。
数据驱动:数据驱动方法根据数据的统计规律推断变化趋势,并最终用于预测和评估交通状态。这种方法不分析交通系统的物理特性和动态行为,具有很高的灵活性。
① 传统数据驱动“参数化”模型:
- 历史平均模型(Historical Average:HA):其中历史时期交通量的平均值用作预测值。优点:该方法不需要任何假设,计算简单快速;缺点:不考虑时间特征,预测精度较低。
- 时间序列模型:将参数模型与观测到的时间序列相匹配,以预测未来数据。早在1976年,Box和Jenkins[5]就提出了自回归积分移动平均模型(ARIMA),这是应用最广泛的时间序列模型。1995年,Hamed等人使用ARIMA模型预测城市干道的交通量。为了提高模型的预测精度,产生了不同的变量,包括Kohonen-ARIMA、子集ARIMA、季节性ARIMA等。Lippi等人将支持向量回归模型与季节性ARIMA模型进行了比较,发现前者(SARIMA)模型在交通拥堵方面具有更好的效果。线性回归模型基于历史交通数据建立回归函数来预测交通流量。
- 卡尔曼滤波模型:根据前一时刻和当前时刻的交通状态预测未来的交通信息。1984年,Okutani和Stephanedes[7]使用Kalman滤波器建立交通流状态预测模型。随后,一些研究[33]、[34]使用Kalman滤波器来实现流量预测任务。
优缺点:传统的参数化模型算法简单,计算方便。然而,这些模型依赖于系统模型是静态的假设,不能反映交通数据的非线性和不确定性,不能克服交通事故等随机事件的干扰。
② 传统数据驱动“非参数化”模型:
(只要足够的历史数据就能自动从交通数据中学习统计规律,从而解决参数化模型不能解决的问题)
- k-nearest neighbor model :
- the support vector regression model(支持向量回归模型):
- the Fuzzy Logic model(模糊逻辑模型):
- the Bayesian network model(贝叶斯网络模型):
- 神经网络;
③ 深度学习(仅考虑时间性):
- Feed Forward NN(前馈神经网络)
- deep belief network (DBN)深度信念网络
- 递归神经网络(RNN)及其变体长期短期记忆(LSTM)和门控递归单元(GRU)可以有效地利用自循环机制,可以很好地学习时间依赖性并获得更好的预测结果;
优缺点:上述模型只考虑了时间特征而忽略了空间相关性,使得交通数据的变化不受城市路网的约束,无法准确预测道路上的交通信息。
④ 深度学习(初步考虑时空):
- SAE模型;
- ST-ResNet
- CNN和LSTM
- ITRCN:CNN+GRU
- 融合卷积长短时记忆网络(FCL-Net)
- 深度卷积神经网络(DCNN)和LSTM
优缺点:CNN基本上适用于欧几里德空间,如图像、规则网格等,并且对具有复杂拓扑结构的交通网络具有局限性,因此不能从本质上描述空间依赖性。
三、METHODOLOGY
1. Problem Definition
在本研究中,交通预测的目标是根据道路上的历史交通信息预测一定时期内的交通信息。在我们的方法中,交通信息是一个通用的概念,可以是交通速度、交通流量或交通密度。在不丧失通用性的情况下,我们在实验部分以交通速度作为交通信息的一个例子。
- Definition 1:路网G: G = ( V , E ) G=(V,E) G=(V,E),描述道路的拓扑结构,每条道路为一个节点,V代表一组节点, V = v 1 , v 2 , ⋅ ⋅ , v n V={v1,v2,··,vn} V=v1,v2,⋅⋅,vn,n是节点的数量;邻接矩阵A用于表示道路之间的连接;邻接矩阵仅包含0和1的元素。0代表两条道路间无连接,1代表有连接;
- Definition 2:特征矩阵: X N ∗ P X ^{N*P} XN∗P,P表示节点属性特征的数量(历史时间序列的长度),特征可以是流量速度密度;这篇文章选择的是速度;
因此,时空交通预测问题可被视为在路网拓扑G和特征矩阵X的前提下学习映射函数f,然后计算接下来T时刻的交通信息,如等式所示:
[ X t + 1 , ⋯ , X t + T ] = f ( G ; ( X t − n , ⋯ , X t − 1 , X t ) ) \left[X_{t+1}, \cdots, X_{t+T}\right]=f\left(G ;\left(X_{t-n}, \cdots, X_{t-1}, X_{t}\right)\right) [Xt+1,⋯,Xt+T]=f(G;(Xt−n,⋯,Xt−1,Xt))
其中n是历史时间序列的长度,T是需要预测的时间序列的长度。
2. Overview
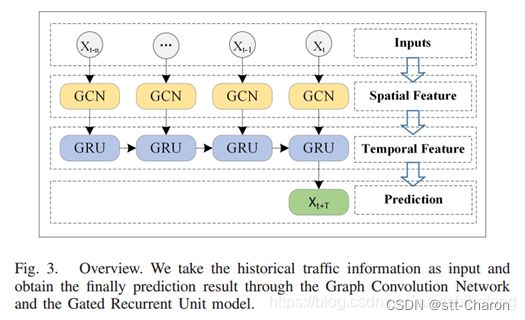
T-GCN模型由两部分组成:GCN+GRU。如图3所示,使用历史n个时间序列数据作为输入,使用图卷积网络捕捉城市道路网络的拓扑结构,以获取空间特征。其次,将获得的具有空间特征的时间序列输入到GRU模型中,通过单元间的信息传递获得动态变化,以获取时间特征。最后,通过全连接层得到结果。
3. Methodology
[1] 空间相关性建模:
获取复杂的空间相关性是交通预测的关键问题。传统的卷积神经网络(CNN)可以获得局部空间特征,但它只能用于欧几里德空间,如图像、规则网格等。城市道路网络是图形形式,而不是二维网格,这意味着CNN模型不能反映城市道路网和道路的复杂拓扑结构,因此,无法准确捕捉空间依赖性。近年来,将CNN推广到可处理任意图结构数据的图卷积网络(GCN)受到了广泛关注。GCN模型已成功应用于许多应用,包括文档分类、无监督学习和图像分类。给定邻接矩阵A和特征矩阵X,GCN模型在傅里叶域中构造滤波器。过滤器作用于图的节点,通过其一阶邻域捕获节点之间的空间特征,然后通过叠加多个卷积层来建立GCN模型,其可表示为:
H ( l + 1 ) = σ ( D ~ − 1 2 A ^ D ~ − 1 2 H ( l ) θ ( l ) ) H^{(l+1)}=\sigma\left(\widetilde{D}^{-\frac{1}{2}} \widehat{A} \widetilde{D}^{-\frac{1}{2}} H^{(l)} \theta^{(l)}\right) H(l+1)=σ(D −21A D −21H(l)θ(l))
选择2层GCN模型[47]来获得空间相关性,其可以表示为:
f ( X , A ) = σ ( A ^ Re L U ( A ^ X W 0 ) W 1 ) f(X, A)=\sigma\left(\widehat{A} \operatorname{Re} L U\left(\widehat{A} X W_{0}\right) W_{1}\right) f(X,A)=σ(A ReLU(A XW0)W1)
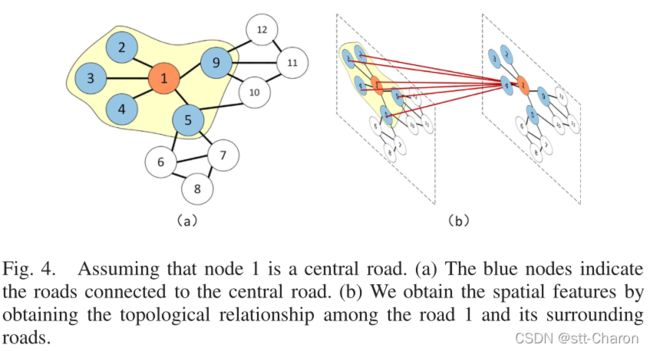
使用GCN模型[47]从交通数据中学习空间特征。如图4所示,假设节点1是中心道路,GCN模型可以获得中心道路与其周围道路之间的拓扑关系,对道路网络的拓扑结构和道路上的属性进行编码,然后获得空间相关性。
[2] 时间相关性建模:
处理序列数据最广泛使用的神经网络模型是递归神经网络(RNN)。然而,由于梯度消失和梯度爆炸等缺陷,传统的递归神经网络模型长时预测工作中存在缺陷。LSTM模型[51]和GRU模型[52]是递归神经网络的变体,已被证明可以解决上述问题。LSTM和GRU的基本原理大致相同[53]。它们都使用门控机制来记忆尽可能多的长期信息,对各种任务同样有效。然而,由于其复杂的结构,LSTM具有较长的训练时间,而GRU模型具有相对简单的结构、较少的参数和较快的训练能力。因此,这篇文章选择GRU模型从流量数据中获取时间依赖性。GRU通过将时刻 t − 1 t-1 t−1 的隐藏状态和当前交通信息作为输入来获取时刻t的交通信息。该模型在捕获当前时刻的交通信息的同时,仍然保持了历史交通信息的变化趋势,并具有捕获时间相关性的能力。
3. Temporal Graph Convolutional Network
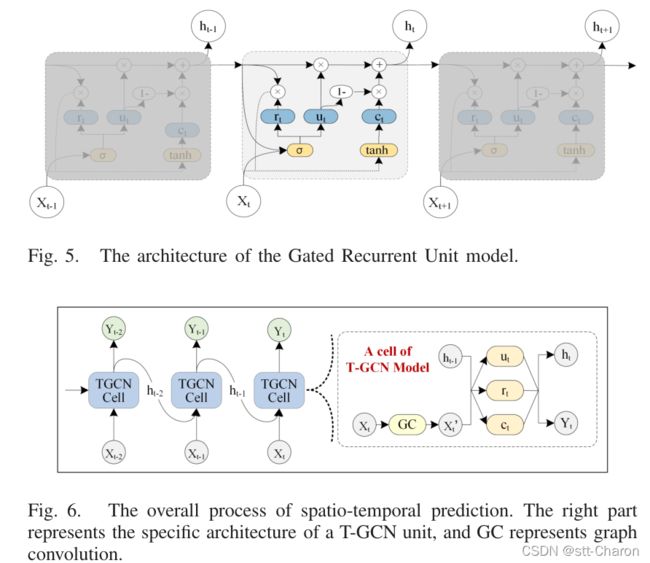
如图6所示,左边是时空预测的过程,右侧的是T-GCN cell的特定结构, ht−1表示t – 1时刻的输出, GC是图卷积过程, ut 和 rt是t时刻的更新门和重置门, ht表示t时刻的输出。(简单来说就是叠加了两个GCN层和一个GRU层)。
四、Experiments
1. 数据集
① SZ-taxi:该数据集包括2015年1月1日至1月31日深圳的出租车轨迹。选取罗湖区156条主要道路作为研究区域。实验数据主要包括两部分。一种是156*156邻接矩阵,用于描述道路之间的空间关系。每行表示一条道路,矩阵中的值表示道路之间的连接。另一个是特征矩阵,它描述了每条道路上的速度随时间的变化。每行代表一条道路;每列是不同时间段道路上的交通速度。我们每15分钟计算一次每条道路的交通速度;
② Los-loop: 该数据集由环路检测器从洛杉矶县高速公路实时采集。2012年3月1日至3月7日,我们选择了207个传感器及其流量速度。我们每5分钟计算一次交通速度。相似性,数据由邻接矩阵和特征矩阵组成。邻接矩阵由交通网络中传感器之间的距离计算得出。由于Los-loop数据集包含一些缺失数据,我们使用线性插值方法填充缺失值。
在实验中,输入数据被标准化为区间[0,1]。此外,80%的数据用作训练集,其余20%作测试集。
2. 评价指标
M为时间样本数;N是道路数
- Root Mean Squared Error (RMSE):
R M S E = 1 M N ∑ j = 1 M ∑ i = 1 N ( y i j − y i j ^ ) 2 R M S E=\sqrt{\frac{1}{M N} \sum_{j=1}^{M} \sum_{i=1}^{N}\left(y_{i}^{j}-\widehat{y_{i}^{j}}\right)^{2}} RMSE=MN1j=1∑Mi=1∑N(yij−yij )2
-
Mean Absolute Error (MAE):
M A E = 1 M N ∑ j = 1 M ∑ i = 1 N ∣ y i j − y i j ^ ∣ M A E=\frac{1}{M N} \sum_{j=1}^{M} \sum_{i=1}^{N}\left|y_{i}^{j}-\widehat{y_{i}^{j}}\right| MAE=MN1j=1∑Mi=1∑N∣∣∣yij−yij ∣∣∣ -
Accuracy:
Accuracy = 1 − ∥ Y − Y ^ ∥ F ∥ Y ∥ F \text { Accuracy }=1-\frac{\|Y-\widehat{Y}\|_{F}}{\|Y\|_{F}} Accuracy =1−∥Y∥F∥Y−Y ∥F -
Coefficient of Determination ( R 2 R ^{2} R2):
R 2 = 1 − ∑ j = 1 M ∑ i = 1 N ( y i j − y i j ^ ) 2 ∑ j = 1 M ∑ i = 1 N ( y i j − Y ˉ ) 2 R^{2}=1-\frac{\sum_{j=1}^{M} \sum_{i=1}^{N}\left(y_{i}^{j}-\widehat{y_{i}^{j}}\right)^{2}}{\sum_{j=1}^{M} \sum_{i=1}^{N}\left(y_{i}^{j}-\bar{Y}\right)^{2}} R2=1−∑j=1M∑i=1N(yij−Yˉ)2∑j=1M∑i=1N(yij−yij )2 -
Explained Variance Score ( v a r var var):
var = 1 − Var { Y − Y ^ } Var { Y } \operatorname{var}=1-\frac{\operatorname{Var}\{Y-\widehat{Y}\}}{\operatorname{Var}\{Y\}} var=1−Var{Y}Var{Y−Y }
3. 模型参数选择
超参数:
- learning rate(学习率):0.001
- the batch size(批量大小):32
- training epoch: 5000
hidden units(隐藏单元数):
在我们的实验中,对于SZ-taxi数据集,我们从[8,16,32,64,100,128]中选择隐藏单元的数量,并分析预测精度的变化。如图7所示,横轴表示隐藏单元的数量,纵轴表示不同度量的变化。图7(a)显示了训练集中不同隐藏单元的RMSE和MAE结果。可以看出,当数字为100时,误差最小。图7(b)显示了不同隐藏单位的精度、R2和var的变化。图7(c)和图7(d)显示了测试集的结果。同样,当数字为100时,结果达到最大值。总之,将该数字设置为100时,预测结果更好。随着隐单元数的增加,预测精度先增大后减小。这主要是因为当隐单元大于一定程度时,模型复杂度和计算难度会大大增加,从而导致对训练数据的过度拟合。因此,我们在SZ-taxi数据集上的实验中将隐藏单元的数量设置为100。
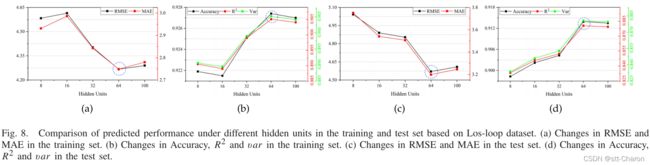
如图8,采用同样的方法对Los-loop数据集设置了64隐藏单元。

3. Experiment Results
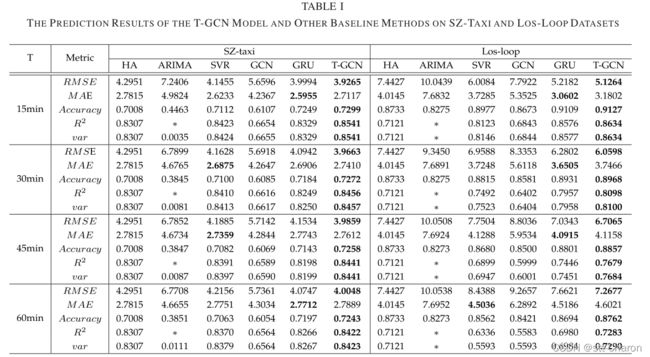
T-GCN模型和其他基线方法在两个数据集上15分钟、30分钟、45分钟和60分钟预测任务的性能。∗ 这意味着数值小到可以忽略不计,表明模型的预测效果较差。
模型特点:
① 预测精度高 :可以发现,基于神经网络的方法,包括强调时间特征建模重要性的T-GCN模型、GRU模型,通常比其他基线(如HA模型、ARIMA模型和SVR模型)具有更好的预测精度。例如,对于15分钟交通量预测任务,与HA模型相比,T-GCN模型和GRU模型的RMSE误差分别降低了约8.58%和6.88%,精确度分别比HA模型高出约4.15%和3.44%。T-GCN模型和GRU模型的RMSE误差分别比ARIMA模型低45.77%和32.97%,两种模型的精度分别提高了63.54%和62.42%。与SVR模型相比,T-GCN和GRU模型的RMSE误差分别降低了5.28%和0.67%,比SVR模型高出约2.63%和1.93%。这主要是由于HA、ARIMA和SVR等方法难以处理复杂的非平稳时间序列数据。GCN模型的预测效果较低是因为GCN只考虑了空间特征,忽略了交通数据是典型的时间序列数据。此外,作为一种成熟的交通量预测方法,ARIMA的预测精度相对低于HA,这主要是因为ARIMA难以处理长期和非平稳数据。通过计算每个节点的误差并求平均值来计算ARIMA;如果某些数据出现波动,也会增加最终总误差。
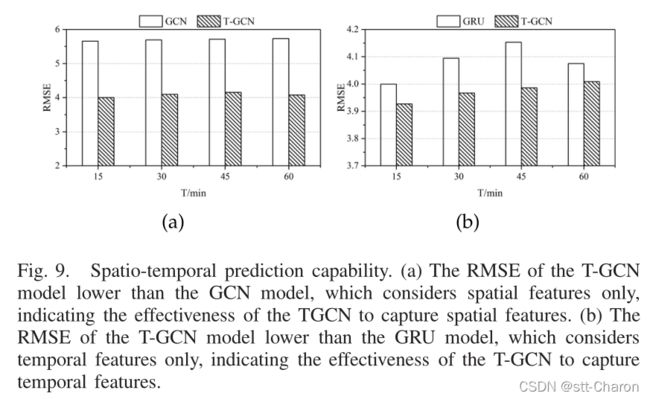
② 时空预测能力 :为了验证T-GCN模型是否能够从交通数据中描绘时空特征,将T-GCN模型与GCN模型和GRU模型进行了比较。如图9所示,我们可以清楚地看到,基于时空特征(T-GCN)的方法比基于单因素(GCN,GRU)的方法具有更好的预测精度,表明T-GCN模型可以从交通数据中捕获时空特征。例如,对于15分钟交通量预测,与仅考虑空间特征的GCN模型相比,RMSE降低了约30.62%;对于30分钟交通量预测,T-GCN模型的RMSE降低了30.32%,表明T-GCN模型可以捕捉空间相关性。与只考虑时间特征的GRU模型相比,对于15分钟和30分钟的交通量预测,T-GCN模型的RMSE误差分别降低了约1.82%和3.12%,表明T-GCN模型能够很好地捕捉时间相关性。
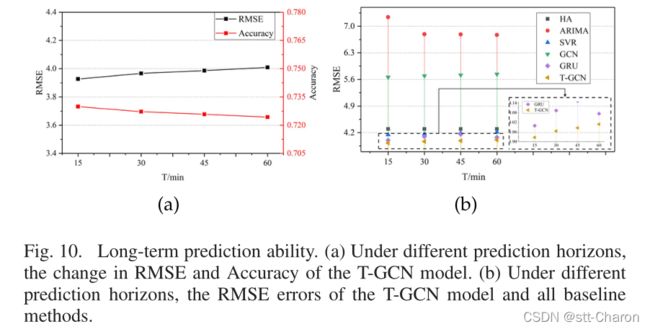
③ 长时预测能力 :无论horizon如何变化,T-GCN模型都可以通过训练获得最佳的预测性能,并且预测结果的变化趋势较小,这表明我们的方法对预测视界不敏感。因此,我们知道T-GCN模型不仅可以用于短期预测,还可以用于长期预测。图10(a)显示了不同预测水平下RMSE和精度的变化,分别代表T-GCN模型的预测误差和精度。可以看出,误差增加和精度下降的趋势很小,具有一定的稳定性。图10(b)显示了不同水平基线的RMSE比较。我们观察到T-GCN模型可以在不考虑预测范围的情况下获得最佳结果。
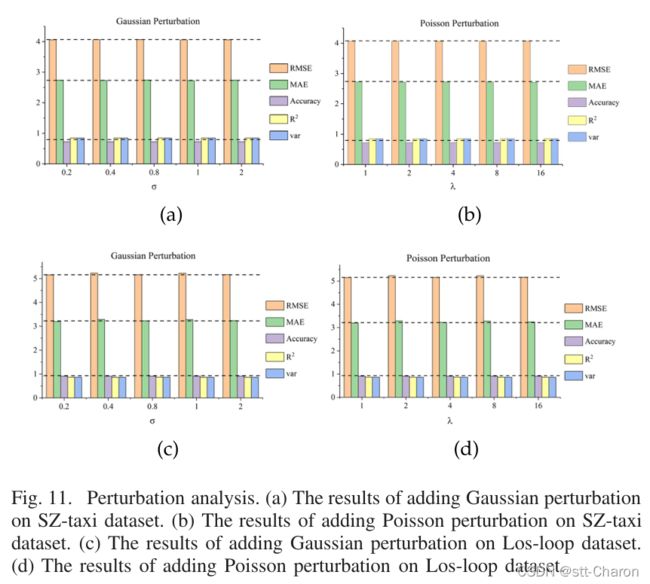
**④ 扰动分析和鲁棒性 ** :在实验数据中加入了两种常见的随机噪声。随机噪声服从高斯分布 N ∈ ( 0 , σ 2 ) N∈(0,σ^2) N∈(0,σ2),其中 σ ∈ ( 0.2 , 0.4 , 0.8 , 1 , 2 ) σ∈ (0.2,0.4,0.8,1,2) σ∈(0.2,0.4,0.8,1,2)和泊松分布 P ( λ ) P(λ) P(λ),其中 λ ∈ ( 1 , 2 , 4 , 8 , 16 ) λ∈ (1, 2, 4, 8, 16) λ∈(1,2,4,8,16)。然后,将噪声矩阵的值归一化为0到1之间。使用不同的评估指标,结果如下所示。图11(a)显示了在SZ出租车数据集上添加高斯噪声的结果,其中横轴表示σ,纵轴表示每个评估指标的变化,不同的颜色表示不同的指标。类似地,图11(b)显示了在SZ出租车数据集上添加泊松噪声的结果。图11(c)和11(d)是在Losloop数据集上添加高斯噪声和泊松噪声的结果。可以看出,无论噪声分布如何,度量的变化都很小。因此,T-GCN模型具有鲁棒性,能够处理高噪声问题。
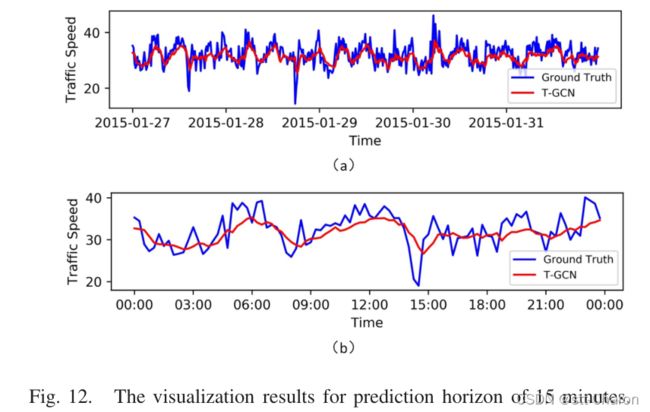
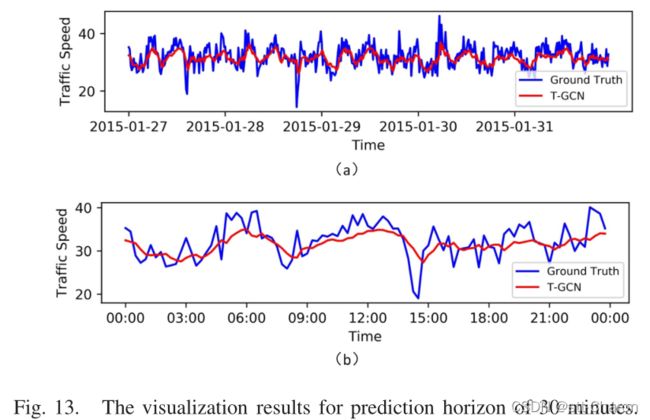
**⑤ 模型解释 ** :为了更好地理解T-GCN模型,在SZ出租车数据集上选择一条道路,并可视化测试集的预测结果。图12、图13、图14和图15分别显示了15分钟、30分钟、45分钟和60分钟预测范围的可视化结果。这些结果表明:
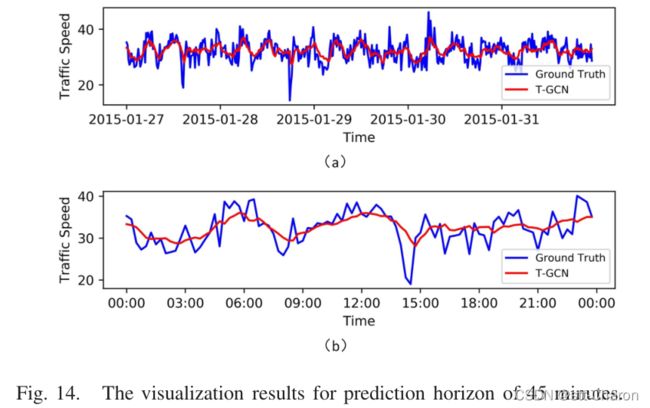
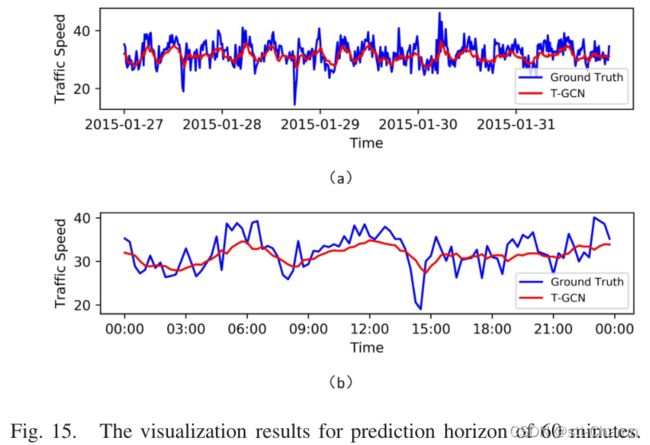
五、 Conclusion
本研究开发了一种新的基于神经网络的交通预测方法T-GCN,该方法将GCN和GRU相结合。我们使用图网络对城市道路网络进行建模,其中图上的节点表示道路,边表示道路之间的连接关系,道路上的交通信息描述为图上节点的属性。一方面,GCN用于捕捉图的空间拓扑结构,以获得空间相关性;另一方面,引入GRU模型来捕捉节点属性的动态变化,以获得时间依赖性。最后,T-GCN模型用于处理时空交通预测任务。在两个真实的交通数据集上进行评估,并与HA模型、ARIMA模型、SVR模型、GCN模型和GRU模型进行比较,T-GCN模型在不同的预测范围下取得了更好的性能。此外,扰动分析说明了我们方法的鲁棒性。总之,T-GCN模型成功地从交通数据中捕获了空间和时间特征,因此可以应用于其他时空任务。
文章可提升的点:
- 以每条道路为节点;
- 每条道路仅考虑道路间的连通性,邻接矩阵仅包含0和1;
- T-GCN模型对局部极小值/极大值的预测较差;(主要原因是GCN模型在傅里叶域中定义了一个平滑滤波器,并通过不断移动滤波器来捕获空间特征。这一过程导致整体预测结果的微小变化,从而使峰值更加平滑)
【交通流预测专栏文章阅读链接】:https://blog.csdn.net/stt666/category_11572284.html?spm=1001.2014.3001.5482