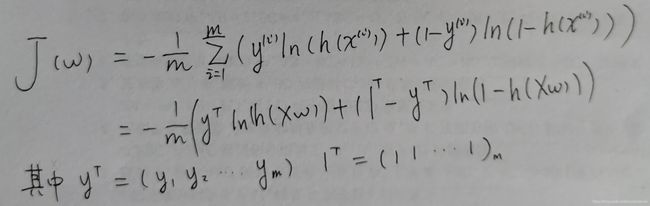机器学习学习笔记（9）----测试logistic回归模型

在《机器学习学习笔记（8）----logistic回归模型》文章中，我们推导出了logistic回归模型的梯度计算的代数公式，为了便于编程计算，我们将其转换成矩阵形式，并得出logistic回归模型的梯度下降迭代公式：

损失函数计算公式的矩阵表示如下：

这样，实现logistic回归模型的批量梯度下降方法的代码如下（gdlogistic.py，源码参考自《Python机器学习算法：原理，实现与案例》）：

import numpy as np

class GDLogisticRegression:

    def __init__(self, n_iter=1000, eta=1e-4, tol=None):
    
        # 训练迭代次数
        self.n_iter = n_iter
        
        # 学习率
        self.eta = eta
        
        # 误差变化阈值
        self.tol = tol
        
        # 模型参数w（训练时初始化）
        self.w = None
    
    def _preprocess_data_X(self, X):
        '''数据预处理'''
        
        # 扩展X，添加x0列设置为1
        m, n = X.shape
        X_ = np.empty((m, n + 1))
        X_[:, 0] = 1
        X_[:, 1:] = X
        
        return X_
        
    def _loss(self, y, y_pred):
        '''损失函数计算'''
        return -(1.0/y.size)*(np.matmul(y.T, np.log(y_pred))+np.matmul((1 - y.T), np.log(1-y_pred)))

    def _gradient(self, X, y, y_pred):
        '''计算梯度'''
        return np.matmul(X.T, y_pred - y)/y.size
    
    def _sigmoid(self, z):
        return 1.0/(1.0+np.exp(-z))
    
    def _predict(self, X, w):
        '''h(x)函数 ：预测y=1的概率'''
        z = np.matmul(X, w)
        return self._sigmoid(z)
        
    def _gradient_decent(self, w, X, y):
        '''梯度下降算法'''
        
        # 若用户指定tol，则启动早期停止法
        if self.tol is not None:
            loss_old = np.inf
            
        # 使用梯度下降，至多迭代n_iter次，更新w
        for step_i in range(self.n_iter) :
            #预测
            y_pred = self._predict(X, w)
            #计算损失
            loss = self._loss(y, y_pred)
            print('%4i Loss:%s' %(step_i, loss))
            
            #早期停止法
            if self.tol is not None :
                #如果损失下降少于阈值，则终止迭代
                if loss_old - loss < self.tol:
                    break
                loss_old = loss
                
            #计算梯度
            grad = self._gradient(X, y, y_pred)
            #更新w
            w -= self.eta * grad
    
    def train(self, X_train, y_train):
        '''训练'''
        
        # 预处理，添加x0列设置为1
        _X_train = self._preprocess_data_X(X_train)
        
        # 初始化参数向量w
        _, n = _X_train.shape
        self.w = np.random.random(n) * 0.05
        
        # 执行梯度下降训练,估算w
        self._gradient_decent(self.w, _X_train, y_train)
        
    def predict(self, X):
        '''预测'''
        
        # 预处理，添加x0列设置为1
        X_predict = self._preprocess_data_X(X)
        y_pred = self._predict(X_predict, self.w)
        
        # 根据概率预测类别，P>=0.5, y=1,否则y=0
        return np.where(y_pred >= 0.5, 1.0, 0.0)

这份代码与《机器学习学习笔记（7）----测试梯度下降方法》中的线性回归的批量梯度下降算法的代码很像，只是改变了梯度下降以及损失函数的计算方法。可以看出，相关的计算梯度下降和损失函数的函数的实现都是按照我们前面给出的矩阵运算公式进行计算，下面测试一下效果。

还是使用葡萄酒网站的数据集（https://archive.ics.uci.edu/ml/machine-learning-databases/wine/），使用wine.data，wine.data对葡萄酒分成3类，我们模型只能处理2类，因此手工删除一类数据（第一列等于3的数据），然后倒入数据：

>>> import numpy as np
>>> X = np.genfromtxt('wine.data', delimiter = ',', usecols= range(1,14))
>>> X
array([[1.423e+01, 1.710e+00, 2.430e+00, ..., 1.040e+00, 3.920e+00,
        1.065e+03],
       [1.320e+01, 1.780e+00, 2.140e+00, ..., 1.050e+00, 3.400e+00,
        1.050e+03],
       [1.316e+01, 2.360e+00, 2.670e+00, ..., 1.030e+00, 3.170e+00,
        1.185e+03],
       ...,
       [1.179e+01, 2.130e+00, 2.780e+00, ..., 9.700e-01, 2.440e+00,
        4.660e+02],
       [1.237e+01, 1.630e+00, 2.300e+00, ..., 8.900e-01, 2.780e+00,
        3.420e+02],
       [1.204e+01, 4.300e+00, 2.380e+00, ..., 7.900e-01, 2.570e+00,
        5.800e+02]])
>>> y = np.genfromtxt('wine.data', delimiter = ',', usecols= 0)
>>> y
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 2., 2., 2., 2., 2., 2., 2., 2., 2.,
       2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2.,
       2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2.,
       2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2.,
       2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2.])

前两类数据等于1或者2，我们希望y=0或者1，因此，再处理一下数据：

>>> y -= 1
>>> y
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

进行训练：

>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
>>> from gdlogistic import GDLogisticRegression
>>> gdlogr = GDLogisticRegression()
>>> gdlogr.train(X_train, y_train)

Warning (from warnings module):
  File "E:\book2\AI\machine learning\gdlogistic.py", line 32
    return -(1.0/y.size)*(np.matmul(y.T, np.log(y_pred))+np.matmul((1 - y.T), np.log(1-y_pred)))
RuntimeWarning: divide by zero encountered in log
   0 Loss:inf
   1 Loss:7.590477955671938
   2 Loss:0.3053558475934125

......

 997 Loss:0.7898755307005065
 998 Loss:1.3638529398103962
 999 Loss:0.787440097813426

然后检查训练效果：
>>> y_predict = gdlogr.predict(X_test)
>>> y_predict
array([0., 1., 0., 1., 1., 1., 0., 0., 1., 0., 1., 1., 0., 1., 1., 0., 1.,
       1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 1., 1., 1., 1., 1.,
       1., 0., 0., 0., 0.])
>>> y_test
array([0., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1.,
       1., 1., 0., 0., 0., 0., 1., 1., 1., 0., 0., 0., 1., 1., 1., 1., 1.,
       1., 0., 0., 0., 0.])

共有5组数据预测错误，说明这个模型还不是很准。

看一下，scikit-learn库封装的logistic回归算法的效果，使用同样的训练数据：

>>> from sklearn.linear_model import LogisticRegression
>>> clf = LogisticRegression()
>>> clf.fit(X_train,y_train)

Warning (from warnings module):
  File "C:\Users\Administrator\AppData\Local\Programs\Python\Python38-32\lib\site-packages\sklearn\linear_model\_logistic.py", line 938
    n_iter_i = _check_optimize_result(
ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.

Increase the number of iterations (max_iter) or scale the data as shown in:
    https://scikit-learn.org/stable/modules/preprocessing.html
Please also refer to the documentation for alternative solver options:
    https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='auto', n_jobs=None, penalty='l2',
                   random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
                   warm_start=False)
>>> y_predict1= clf.predict(X_test)
>>> y_predict1
array([0., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1.,
       1., 1., 0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 1., 1., 1., 1., 1.,
       1., 0., 0., 0., 0.])
>>> clf.score(X_test,y_test)
0.9743589743589743

效果比我们编写的算法预测结果要准确，只错了1组数据。

参考资料：

《快乐机器学习》

《Python机器学习算法：原理，实现与案例》

《机器学习算法数学解析与Python实现》