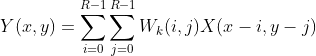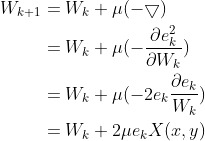图像处理：TDLMS算法原理介绍及MATLAB实现
一、TDLMS介绍
1.1 算法原理
二维最小均方（two-dimensional least mean square, TDLMS）滤波算法由最小均方误差（least mean square error, LMS)滤波器（即维纳滤波器）演变而来。
TDLMS算法的应用方向：
- 自适应背景预测
- 平滑降噪
- 目标检测
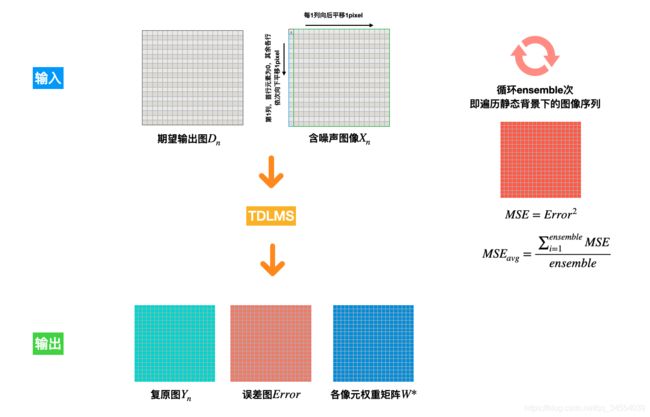
算法依据是：图像和噪声都是随机变量，力图找到一个不含噪声的图像估计，使得含噪声的图像与复原后的图像均方差最小。算法原理如图1所示。
图1 TDLMS算法原理框图
1.2 算法步骤
第一步：对每个像元逐个计算复原图像
对于大小为M*N的输入图像X，设置R*R的滤波器窗口，按照从左至右、从上至下对每一个像元进行估计，对于任意的像元(x, y)，其估计值Y(x, y)表示形式如下（即模板W与含噪声图像作卷积）：
…………………………（1）
式中，
表示各个像元的坐标，
滤波器利用每次迭代更新权重矩阵
，这里 
表示权重矩阵的序号，按照“从上至下，从左至右”的迭代顺序，
.
第二步：将复原图像与期望图像作比较，得到误差信号
将复原图像
与期望输出
作比较，得到每次迭代的误差：
…………………………（2）
关于期望输出
The desired output
is the pixel next to or several steps ahead of it. Therefore, the desired image is a shifted version of the original one. [2]
第三步：利用误差信号，结合“最小均方差”和“最陡下降法”更新权重矩阵W
TDLMS算法优化原理是“最小均方误差”，即令![E[e_j^2]](http://img.e-com-net.com/image/info8/4403cd3c8f994ae0a5689ed8578e11fe.gif){kind=small}
最小化，这里用到的算法是“最速下降法steepest decent method”，因此权重矩阵优化公式为：
…………………………（3）
式中，
为迭代步长；
为公式（2）中所求误差。
均方误差的性能曲面：
均方误差的性能曲面是L+2维空间中一个中间下凹的超抛物面
，有唯一的最低点，该曲面成为均方误差的性能曲面。
自适应过程：自动调整系数使均方误差达到最小值
最陡下降法：
即沿性能曲面最陡方向向下搜索曲面的最低点；性能曲面的最陡下降方向即曲面的负梯度方向
。
最陡下降法迭代搜索过程：
从曲面上某一初始点（对应初始权重）出发，沿该点负梯度方向搜索至第1点
，以此类推，直至搜索出曲面最低点
。
因此，最陡下降法的迭代公式为：
，
式中
为曲面各点的梯度，是迭代次数（or 时间）n的函数。
LMS算法：
核心思想：用平方误差代替均方误差，即
公式（3）的推导：
![e^2(n)\approx E[e^2(n)]](http://img.e-com-net.com/image/info8/220496159e94478a9cf1a943f36f2872.gif){kind=small}
1.3 总结与思考
1.3.1 TDLMS算法伪代码
function out_img = TDLMS (input, desired_img, step, W_0)
for 遍历图像中每一个像素点（迭代次数 = 像素数）
Y(k) = W(k)*X(k);
E(k) = D(k) - Y(k);
W(k+1) = W(k) + step * E(k) * X(k)
end
end1.3.2 TDLMS算法本质上可看作自适应滤波器
自适应滤波器：一种能够根据输入数据和噪声的统计特征自动调整参数，始终保持最优性能的滤波器。
具有两个特点：（1）学习能力，能够在迭代过程中逐步了解和正确估计这些统计特征；（2）跟踪能力，能够及时调整自己的参数，迅速跟踪统计特性的变化。
1.3.3 TDLMS如何利用自适应滤波器的思想进行目标检测？
TDLMS算法考虑当前像元和像元邻域的灰度特性，根据邻域像元的信号和噪声统计特性来估计当前像元的统计特性。当权重矩阵（扫描窗口）移动到背景像元时，由于背景区域的灰度连续性，背景像元的灰度特性具有较强的相关性，当前估计值与期望输出差别不大，算法容易收敛；而当扫描窗口移动到目标像元时，由于目标与背景的灰度特性差异较大，且目标尺寸很小，导致扫描窗口在移出目标区域前都不能收敛至最优值，此时对目标区域的像元估计仍然保留其周围邻域的像元特性，因此得到的复原图像起到了“过滤目标”的作用。
因此，TDLMS可以归类为“基于背景预测的目标检测算法”。
基于背景预测的目标检测算法的主要思想：
Since targets have a small spatial spread while the correlated slutter around can have a much larger spatial extent, an important idea in small target detection is try to predict the background covered by small targets using the correlation information, afterwards by substrcting the predicted image from the original one, the targets can be found easily in the residue image.[2]
目标面积小，而背景面积大且灰度具有连续性，因此利用背景灰度的连续性预测目标区域的背景，得到背景预测图；
原图与背景图作差，得到目标图。
这里也基于另一个理论假设：含目标的图像数学模型为
（不考虑噪声）
但是因为得到的真实图像序列一定含有噪声，且噪声具有随机性，无法准确获得噪声的统计特性，所以背景预测类的算法致力于提高算法的抗噪性和鲁棒性，以降低目标检测的虚警率。
1.3.4 TDLMS算法收敛步长的选择
TDLMS算法的“跟踪性能”很大程度上取决于步长；步长的大小决定的算法的收敛速度。
- 步长越大，算法收敛速度越快，对图像的预测越精确，包括目标区域，进而对作差图像进行检测时目标被忽略。
- 步长越小，算法的收敛速度越慢，检测到目标区域时，往往算法还来不及收敛，滑动窗口已经移出该区域了；但步长过小也会造成图像中很多非平稳区域被忽略，比如背景边缘、强噪声区域，进而导致检测虚警率提高。
因此，理想状态下，步长需要做到在处理目标像元时变小，算法收敛减慢；而在处理背景边缘时变大，加快算法收敛。
1.3.5 TDLMS算法的缺陷
1. 步长的选择（见1.3.4分析）
2. 对图像的预测仅依赖于滑动窗口范围内的像元[2]
理想状况下，我们是利用背景灰度的连续性与相关性来预测被目标覆盖的背景区域，因此理想的结果是使用目标周围背景的统计特性去预测被目标遮盖的背景，以替代“目标区域”以得到较为理想的背景。
但是当滑动窗口覆盖了大部分的目标区域时，优化算法会认为该区域与临近区域不同，并开始向“目标”的特性进行预测和优化，由此预测得到的被目标覆盖的“背景区域”的统计特性会受到目标特性的干扰，相应地，在得到的作差图像中，目标特性将被削弱，造成目标漏检的可能性增大。
因此，我们希望滑动窗口可以“意识到”当前扫描区域为目标区域，进而放弃跟踪直接用周围邻域的值去替换该区域。要达到这一目的，必须考虑更多目标邻近区域的信息。
基于上述分析，文献[2]提出了改进算法。（本文只介绍经典的TDLMS算法及其实现，对其改进算法不作过多赘述。）
二、MATLAB代码实现
这里是对文献[1]中提到的经典TDLMS算法的实现。
2.1 TDLMS算法实现
由图1 TDLMS算法框图易知：
- 算法输入包括：含噪声图像
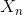，期望输出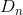，初始权重矩阵
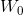，算法迭代步长 - 算法输出：复原图像 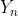（即预测背景图）， 误差图，最后一次迭代得到的“最优”权重矩阵
function [outputImage, errorImage, coefficientBlock] = TWDLMS(input,desired,S)
%% input : 含噪声图像
%% desired: 期望输出
%% S: step -- 迭代步长； filterOrderNo -- 权重矩阵大小R ；initialCoefficients -- 权重矩阵初始值W0
nCoefficients = S.filterOrderNo; % 权重矩阵的边长 R
[nIterationsm,nIterationsn] = size(input); % 输入的图像大小 M*N
nIterations = nIterationsm*nIterationsn; % 迭代次数 = 图像的像素数
% Pre-allocations
errorImage = zeros(nIterationsm, nIterationsn); % 误差图 E
outputImage = zeros(nIterationsm, nIterationsn); % 预测图 Y
coefficientBlock = zeros(nCoefficients,nCoefficients,nIterations); % 权重矩阵R*R, 保存每个像元的权重矩阵W
itCount = 1;
% Initial state of the weight vector
coefficientBlock(:,:,1) = S.initialCoefficients; % 初始化权重矩阵
% Prefixed input
prefixedimage = input;
prefixedimage(:,(nIterationsn+1):(nIterationsn+S.filterOrderNo)) = 0; % 扩充（这里是为了权重矩阵和图像作卷积作预处理）prefixedimage,若原图的大小为M*N，滤波矩阵的大小为F，则prefixedimage的大小为(M+F) * (N+F)
prefixedimage((nIterationsm+1):(nIterationsm+S.filterOrderNo),:) = 0;
% Body
for i1 = 1:nIterationsm
for i2 = 1:nIterationsn
% Y = W * X （卷积）
regressor = prefixedimage(i1+(nCoefficients-1):-1:i1, i2+(nCoefficients-1):-1:i2);
ex1 = coefficientBlock(:,:,itCount).*regressor;
outputImage(i1,i2) = sum(ex1(:));
% 求误差
errorImage(i1,i2) = desired(i1,i2) - outputImage(i1,i2);
% 更新权重矩阵
coefficientBlock(:,:,itCount+1) = coefficientBlock(:,:,itCount) + (2*S.step*errorImage(i1,i2)*regressor);
itCount = itCount+1;
end
end2.2 算法测试
第一步：生成含不同灰度级和测试图。
% 生成图像的大小为96*96
imm = 96;
imn = 96;
v1 = 0.8*ones(imm-25,1);
v2 = 0.2*ones(imm-25,1);
D1 = diag(v1,25);
D2 = diag(v2,-25);
image = zeros(imm,imn);
image(9:88,9:88) = 0.7;
image(17:80,17:80) = 0;
image(27:70,27:70) = 1;
image(32:65,32:65) = 0.2;
image(41:56,41:56) = 1;
for i = 1:imm
for j = 1:imn
if D1(i,j) > 0
image(i,j) = D1(i,j);
end
if D2(i,j) > 0
image(i,j) = D2(i,j);
end
end
end第二步：初始化参数，生成复原图像
% 参数初始化
ensemble = 100;
mu = 35*10^(-5); % 迭代步长
N = 3;
inicoefs = fspecial('gaussian',[3 3]); % 初始化权重矩阵
% inicoefs = zeros(3);
MSE = zeros(imm,imn,ensemble); % 误差E
errim = zeros(imm,imn,ensemble);
for l = 1:ensemble
noiseim = imnoise(image,'gaussian'); % 加入高斯噪声
% 生成期望输出D
for i = 1:imm
for j = 1:imn
if i == 1 && j == 1
prefixedimage(i,j) = 0;
elseif j == 1 && i ~= 1
prefixedimage(i,j) = noiseim(i-1,imn);
else
prefixedimage(i,j) = noiseim(i,j-1);
end
end
end
S = struct('step',mu,'filterOrderNo', N,'initialCoefficients',inicoefs);
[outim, errim(:,:,l), coefs(:,:,:,1)] = TWDLMS(prefixedimage,noiseim,S);
MSE(:,:,l) = MSE(:,:,l)+(errim(:,:,l)).^2;
end
MSE_av = sum(MSE,3)/ensemble;
% 分别绘制原始图像、含噪声图像、复原图像及误差图
figure;
subplot(2,2,1),imshow(image,[]);
title('Original Image');
subplot(2,2,2),imshow(noiseim,[]);
title('Noisy Image');
subplot(2,2,3),imshow(outim,[]);
title('Output Image');
subplot(2,2,4),imshow(MSE_av,[]);
title('MSE Image');
% 对比原始含噪声图像、复原图像和期望输出某一行像素值的变化
% 对照可看出算法的复原效果
figure;
subplot(3,1,1),plot(image(48,:));
title('Original Image Crossection');
subplot(3,1,2),plot(outim(48,:));
title('Output Image Crossection');
subplot(3,1,3),plot(noiseim(48,:));
title('Noisy Image Crossection');
图3 背景复原算法流程
2.3 结果分析
2.3.1 测试结果
图4 从上至下、从左至右依次为：生成的含不同灰度的原始图像；添加了高斯噪声的图像；TDLMS算法输出的复原图像；均方误差图
从均方误差图可以看出，TDLMS算法在边缘处的均方误差比较大，根据上文分析易知，边缘与其邻域的灰度差较大而相关性较小，当滑动窗口扫描至边缘处时，算法不能及时收敛，因此与原图相比，边缘处的均方误差较大。
图5 图像某一行的像素值分布，横坐标为像素所在列数，纵坐标为归一化灰度值
由图5可以看出，复原图像达到了较好的去噪效果，体现了TDLMS算法的平滑降噪性。
2.3.2 测试不同的步长
图6 不同迭代步长下的均方误差分布图
由图6易知，随着迭代步长的增大，权重矩阵的收敛速度变快，当扫描窗口滑动至背景边缘处时，预测像素值迅速学习并跟踪边缘的灰度统计特征，并向其收敛，因此背景边缘处的复原效果更接近真实图像，均方误差较小；反之，随着迭代步长的减小，权重矩阵的收敛速度变慢，当扫描窗口滑动至背景边缘处时，算法还没来得及向边缘像素的统计特征收敛，扫描窗口就滑出了该区域，使得复原图像中的边缘灰度更接近边缘周围邻域灰度，得到的复原图像更平滑，进而使得边缘处均方误差增大。
参考文献
[1] M. M. Hadhoud and D. W. Thomas, “The Two-Dimensional Adaptive LMS [ TDLMSj Algorithm,” vol. 35, no. 5, 1988.
[2] Y. Cao, R. Liu, and J. Yang, “Small target detection using Two-Dimensional Least Mean Square (TDLMS) filter based on neighborhood analysis,” Int. J. Infrared Millimeter Waves, vol. 29, no. 2, pp. 188–200, 2008.