线性回归模型——梯度下降算法
目录
-
- 引言
- 线性回归介绍
- 手动实现梯度下降法线性回归
- 调用API接口实现线性回归
引言
线性回归可能是我们接触最早的机器学习算法了,在高中数学的课本上,我们第一次正式认识这位朋友,通过最小二乘法来得到数据的线性回归方程,进而求得模型的参数。但其实,在初中时,我们就学过通过两个已知点坐标求解一次函数的技能,这也算是线性回归模型的一种特例吧。今天来给大家介绍另一种求解线性回归模型的方法——梯度下降法。
线性回归介绍
- 线性回归定义
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
- 举个例子
老黄勤勤恳恳打工数n年,终于攒下点儿小钱,想拿来买房~统计某楼盘数据如下:

把这些数据点绘制到坐标轴上,可以看出,房屋面积和房屋价格大致呈线性分布,即大致分布在一条直线上。如果能求出这条直线的方程,那么就能根据一个房屋的面积预测它的价格。

线性回归简化流程如下
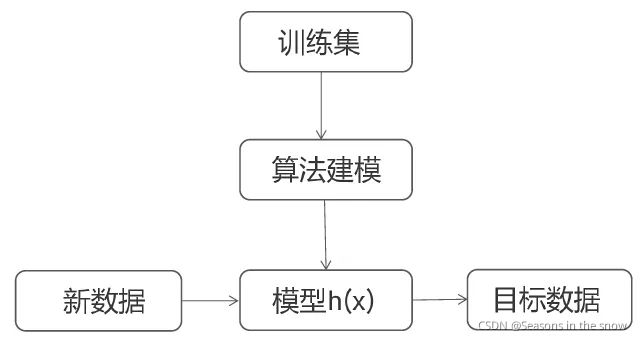
其中,h(x)为:

目标:找到一条最好的拟合线,使得误差最小,也就是代价函数最小。代价函数(cost function)为:

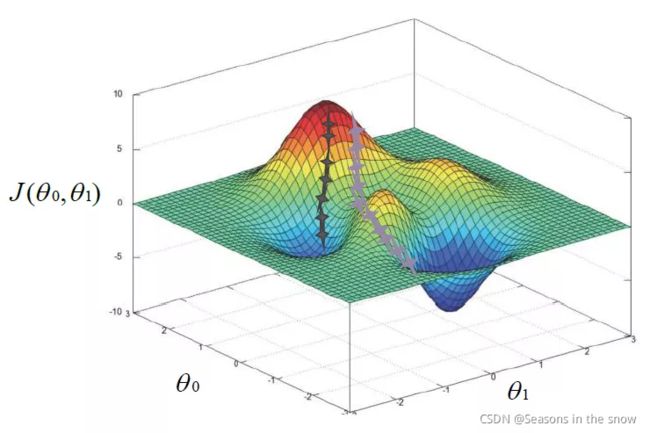
代价函数与θ0,θ1的关系如图所示:

- 梯度下降法介绍
梯度下降法就是可以使代价函数最小化的算法,即寻找合适的θ0、θ1使得代价函数J(θ0,θ1)最小,实现步骤为:
1.初始化θ0,θ1;
2.不停地改变θ0,θ1使得J(θ0,θ1)减小;
3.直到找到J(θ0,θ1)的最小值或局部最小值。
重复如下操作:
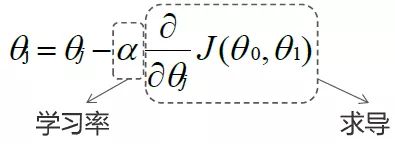
同时更新:
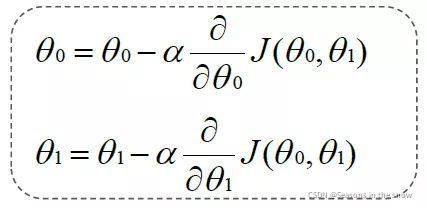
将h(x)代入式子得:
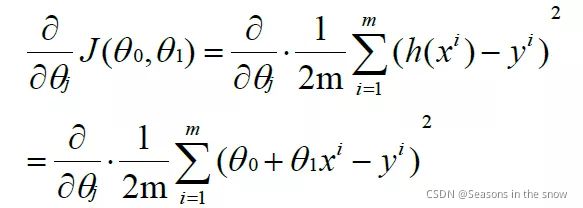
对θ0求偏导:
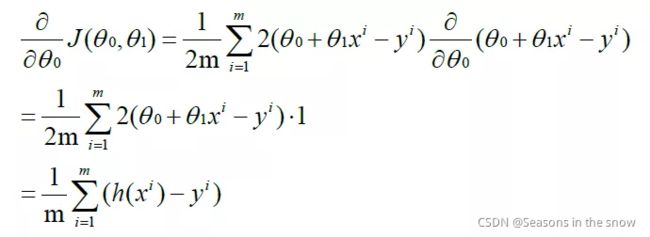
对θ1求偏导:
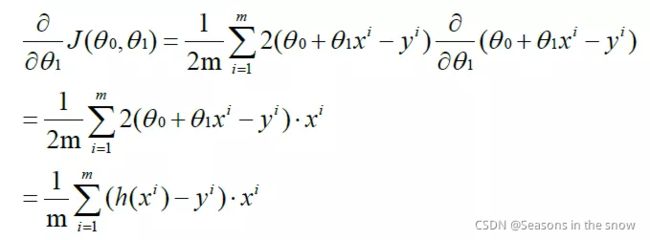
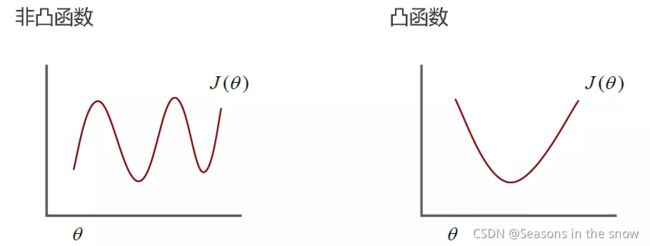
对于凸函数来说,梯度下降法一般能得到唯一最优解,对于非凸函数,可能会陷入局部最优解。
接下来就使用numpy手动实现梯度下降法线性回归,然后调用sklearn接口实现线性回归。
手动实现梯度下降法线性回归
1、导入可能需要用到的库,导入csv数据文件,定义x变量和y变量,绘图显示x,y数据分布情况。
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一(替换sans-serif字体)
plt.rcParams['axes.unicode_minus'] = False # 步骤二(解决坐标轴负数的负号显示问题)
data = np.loadtxt('data.csv',delimiter=',')
x_data = data[:,0]
y_data = data[:,1
plt.scatter(x_data,y_data,marker='x',color='red')
plt.show()
输出结果如下,可以看出,x和y大致呈现线性分布。
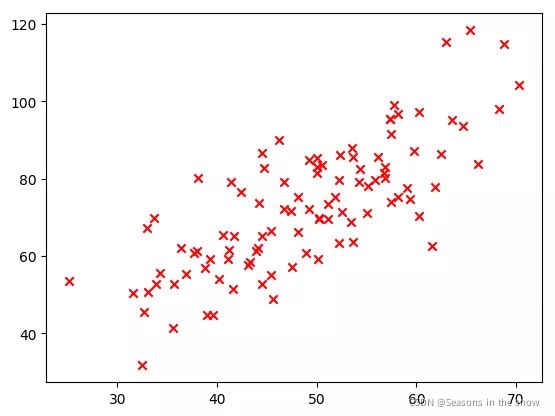
2、定义学习率、初始截距和斜率、迭代次数,定义代价函数计算方法
learning_rate = 0.0001
b = 0
k = 0
n_iterables = 50
def compute_mse(x_data,y_data,k,b):
mse = np.sum((y_data-(k*x_data+b))**2)/len(x_data)/2
return mse
3、定义梯度下降函数,需要将x、y、初始截距、初始斜率、学习率、迭代次数作为参数传入,最终输出结果为目标截距、目标斜率,代价函数值列表。
def gradient_descent(x_data,y_data,k,b,learning_rate,n_iterables):
m = len(x_data)
start_loss = compute_mse(x_data,y_data,k,b)
loss_value = [start_loss]
for i in range(n_iterables):
b_grad = np.sum((k*x_data+b)-y_data)/m
k_grad = np.sum(((k*x_data+b)-y_data)*x_data)/m
b = b - (learning_rate*b_grad)
k = k - (learning_rate*k_grad)
loss_value.append(compute_mse(x_data,y_data,k,b))
print(b,k)
return b,k,np.array(loss_value)
4、调用函数,得到结果,绘图。
b1,k1,loss_list = gradient_descent(x_data,y_data,k,b,learning_rate,n_iterables)
y_predict = k1*x_data+b1
print(b1,k1)
plt.scatter(x_data,y_data,marker='x',color='red')
plt.plot(x_data,y_predict)
plt.show()
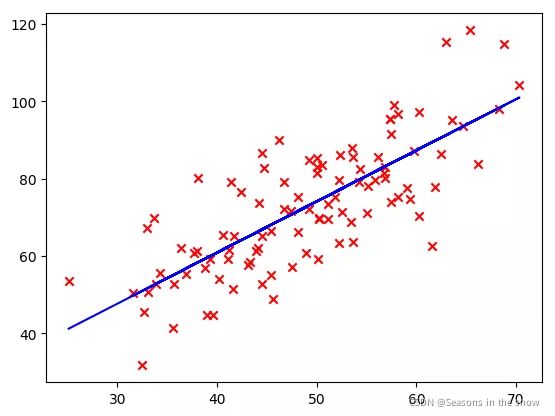
输出结果b1=0.03056,k1=1.47889
如图,看着感觉还可以。
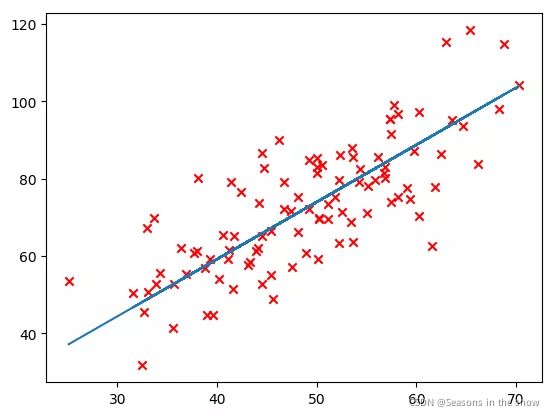
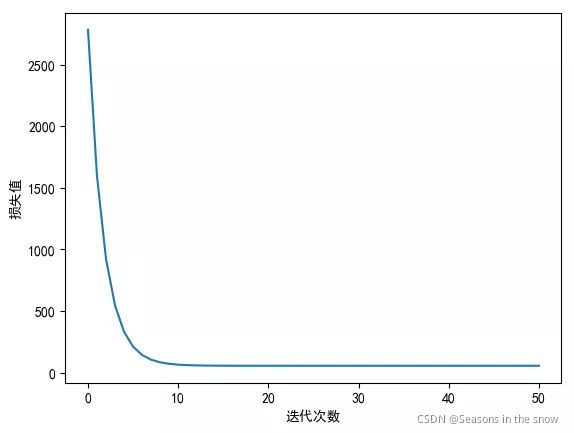
5、画出代价函数随迭代次数变化的曲线,如图所示,可以看出,经过10次迭代后,代价函数的变化就比较小了。
plt.plot(range(n_iterables+1),loss_list)
plt.xlabel('迭代次数')
plt.ylabel('损失值')
plt.show()
调用API接口实现线性回归
1、同样导入可能需要用到的库,导入csv数据文件,定义x变量和y变量,绘图显示x,y数据分布情况。
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
data = np.loadtxt('data.csv',delimiter=',')
x_data = data[:,0,np.newaxis]
y_data = data[:,1]
plt.scatter(x_data,y_data,marker='x',color='red')
plt.show()
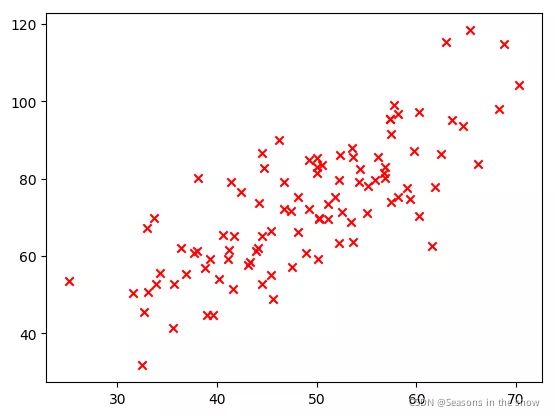
2、定义模型,进行拟合,然后预测,得到结果,进行绘图,可以看到,调用API接口步骤非常简单。
model = LinearRegression()
model.fit(x_data,y_data)
y_predict = model.predict(x_data)
plt.scatter(x_data,y_data,marker='x',color='red')
plt.plot(x_data,model.predict(x_data),'b')
plt.show()
b = model.intercept_
k = model.coef_[0]
print(b,k)
输出:b=7.99102,k=1.322431,与上面得到的结果还是有一些差异的,因为上面只迭代了50次,而调用接口得到的是精确解。