Q-Q图原理详解及Python实现
【导读】在之前的《数据挖掘概念与技术 第2章》的文章中我们介绍了Q-Q图的概念,并且通过调用现成的python函数, 画出了Q-Q图, 验证了Q-Q图的两个主要作用,1. 检验一列数据是否符合正态分布 2. 检验两列数据是否符合同一分布。本篇文章将更加全面的为大家介绍QQ图的原理以及自己手写函数实现画图过程
本文的代码文件(jupyter)和数据文件可以在我们的公众号"数据臭皮匠" 中回复"QQ图"获取
Q-Q图是什么
QQ图是quantile-quantile(分位数-分位数图) 的简称,上面也有介绍它的两个主要作用:
1.检验一列数据是否符合正态分布
2.检验两列数据是否符合同一分布
Q-Q图的原理
要弄清Q-Q图的原理,我们先来介绍下分位数的概念。这里我们引用下百度百科的介绍:
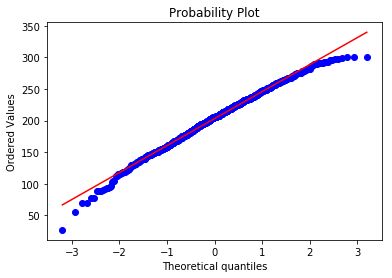
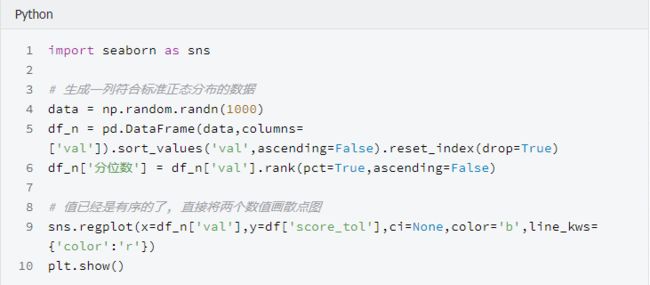
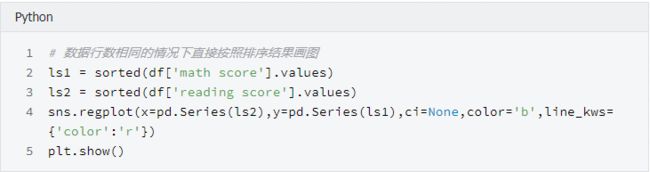
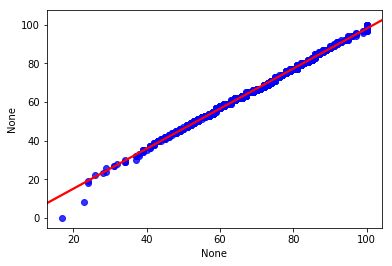
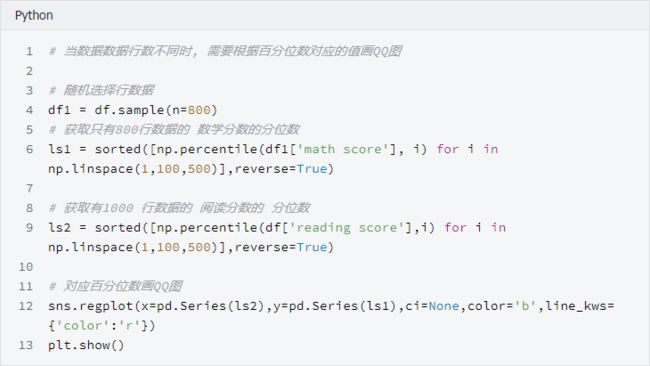
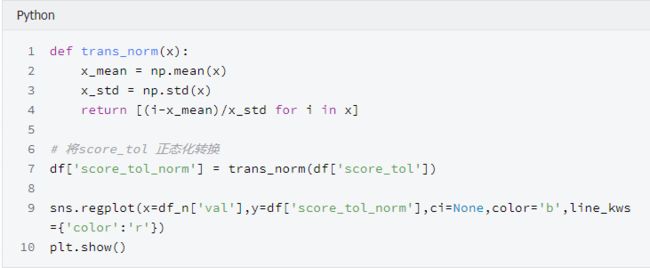
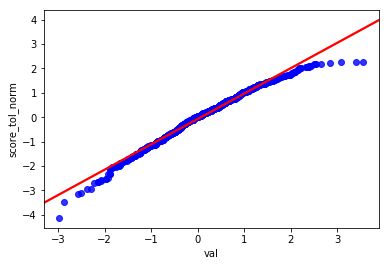
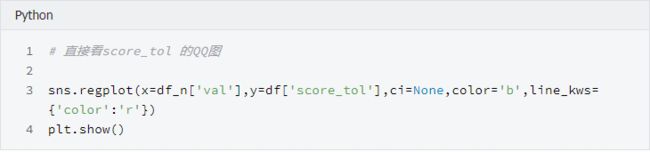
分位数, 指的就是连续分布函数中的一个点,这个点对应概率p。若概率0 What...?? 是不是感觉有点抽象,别着急,我们继续往下看分位数的实例-百分位数。 百分位数,统计学术语,如果将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数。可表示为:一组n个观测值按数值大小排列。如,处于p%位置的值称第p百分位数。 给大家举个例子:初三年级有1000名学生, 期末考试成绩按照从高到低的顺序排列, 排名第10的同学, 刚好位于全校1000名同学的1%处, 他的分数就是全校期末考试分数的第1百分位数, 记为P1, 同理, 第20名同学对应的分数就是第2百分位数P2, ... 第990名同学的分数为第99百分位数 P99。 那么Q-Q图的原理就是,通过把一列样本数据的分位数与已知分布的一列数据的分位数相比较,从而来检验数据的分布情况。所以, Q-Q图的两个功能都是比较两列数据的分位数是否分布在y=x的直线上。当两列数据行数相同时, 首先将两列数据分别从高到低排序, 直接画散点图就可以了, 当两列数据行数不一样时, 需要分别计算出每列数据的百分位数, 再将两列数据的百分位数画散点图, 检查散点图是否分布在y=x直线附近。 我们接下来的实例数据及引用自自kaggle的Students Performance in Exams , 你可以在我们公众号后台回复"QQ图"来获取它。 首先来介绍一下我们的数据集。数据共1000行, 8列, 每行代表一名学生的属性信息, 最后三列为三科成绩, 分别是: 'math score', 'reading score', 'writing score' , 我们将只适用最后三列的分数, 验证学生分数是否符合正态分布 我们先通过调用python包来画QQ图 检验是否符合正态分布 可以看到, 学生的三科总分与标准正态分布的数值画出的散点图, 基本分布在一条直线附近, 可以认为学生分数符合正态分布, 但不是标准正态分布,详细分析我们在下文会讲到。 接下来,我们通过手动画Q-Q图 来实现检验数据是否符合正态分布 当两列数据行数相同时,直接将分别排序后的两列数值画散点图 可以看到, 我们画出了和统计包几乎一样的QQ图(最左侧和最右侧之间的差异, 是由于正态分布变量是随机产生的, 每次都会有一些不同) 直接将分别排序后的两列数值画散点图, 好像不能体现Q-Q图的本质, 我们接下来取0到100的500个分位数,画图看下情况 我们画出了和上面几乎一样的图, 但是可以看到, 右侧的点分布在在直线下方, 结果是符合直觉的, 因为正态分布的数据在最右侧需要有一些比较大的数字, 但是学生成绩被总分300 限制住了, 这就印证了一句话,学霸只能考100是因为满分只有100 两列数据行数相同时 两列数据行数不同时 可以看到, 'math score' 和 'reading score' 两列的分位数分布在y=x 直线附近, 我们可以认为两列数据符合同一分布。 在上面检验数据是否符合正态分布时,我们说, 学生分数符合正态分布, 但不是标准正态分布。是因为通过仔细观察会发现, 散点图并不是沿着y=x 线分布, 而是沿着 y=ax+b 分布, 即, 一条有截距且有斜率的直线。 Q-Q散点图是沿着y=x分布时, 符合标准正态分布 Q-Q散点图沿y=ax+b分布时, 符合正态分布, 但非标准正态分布 可以看到, 散点图基本在y = ax+b 的附近分布, 这时我们可以说,score_tol 列符合正态分布, 但不是标准正太分布。 一般认为,Q-Q图的散点需要分布在y=x 直线附近才认为符合正态分布, 为什么散点图分布在y=ax+b附近, 仍然可以认为, score_tol 符合正态分布呢? 因为, 从图中可以看到, score_tol 列可以写成正态分布的列val 的线性函数 score_tol = a * val + b 而正态分布的性质决定了, 如果一个变量x服从正态分布, 那么他的函数ax+b 也符合正态分布。 本文的Python代码和数据文件可以在我们的公众号"数据臭皮匠" 中回复"QQ图"获 取 长按二维码关注"数据臭皮匠" 作者:范小匠 审核:灰灰匠 编辑:森匠
检验数据是否符合正态分布
检验两列数据是否符合同一分布
符合正态和标准正态分布的区别