一篇NS SAR ADC的学习记录

一篇NS SAR ADC的学习记录

内容包含：

• OverSampling
• Noise Shaping
• Dynamic Amplifier
• DAC with Redundancy

最近看了些有意思的SAR ADC结构，但是因为确实对模拟这个领域不太熟，导致了一系列的级联查找，最终达到了一个大概能懂的状态，为了理清思路，顺便别让看了这么些天的东西浪费了，还是计划写篇文章。

ps：由于不是一篇特别正紧的报告，参考文献就写的比较随便，且我还是个做数字的

A 13.5-ENOB, 107-μW Noise-Shaping SAR ADC With PVT-Robust Closed-Loop Dynamic Amplifier[1]

首先这是一篇JSSC，怕出现一些问题，具体的文章PDF我这里就不提供了，各位可以去IEEE查看这篇文章的原文。

从文章的题目入手，可以看出这个SAR ADC的一些特点，

• ENOB（Effective Number of Bits），一种评判ADC性能的指标；
• 107-μW，指功耗，虽然不知道行业的平均水平，但是能写在题目里应该是比较好的（？）；
• Noise-Shaping，一种在ADC领域首先被运用于Delta-Sigma ADC上降低某些噪声的方法，通过我查到的一些资料，发现这种方案在最近的一些年内与SAR ADC的结合越来越多，形成了一些有趣的运用；
• PVT-Robust，即process voltage temperature，对于这些的变化不敏感，因为这个内容与电路的抽象设计关系不是非常紧密，所以后文也就不详细介绍了；
• Dynamic Amplifier，这是我在这篇文章中看下来觉得最有意思的点，本来我对于动态的各种电路的设计思路就很感兴趣，因此我顺便多看了一些这方面的资料

ADC的各类性能指标汇总[2]

• SNR，信噪比，单位为dB，是输入信号和噪声的平均功率之比
  $$SNR=10\times \log \left(\frac{P_{\text{signal }}}{P_{\text{noise }}}\right)$$

• SINAD（Signal to Noise and Distortion Ratio），信号对噪声的失真比值，单位为dB，是输入信号和所有输出信号失真（包括谐波成分，不包括直流）的功率之比，用于评估输出信号所有传递函数的非线性加上系统所有噪声（量化、抖动和假频）的累积效果
  $$SINAD=10\times \log \left(\frac{P_{\text{signal }}+P_{\text{noise }}+P_{\text{distortion }}}{P_{\text{noise }}+P_{\text{distortion }}}\right)$$

• ENOB（Effective Number of Bits），有效位数，单位为bit，用于描述ADC/DAC系统的有效分辨率。对于理想的N位ADC系统，其ENOB应当无限接近N，但真实电路会不可避免的引入噪声，从而降低ADC的实际分辨率，其值可以使用SINAD算出
  $$ENOB=\frac{SINAD-1.76dB}{6.02dB}$$

Noise Shaping，噪声整形

要说Noise Shaping就最好还是从Delta-Sigma ADC入手，毕竟大概算是个发源地。这部分内容的东西网上有不少，但是我觉得看了很多博客和Paper，还是这篇 Delta-Sigma analog-to-digital converter[3] 的个人网站博客写的最清楚，在这里也推荐给想要了解的人。

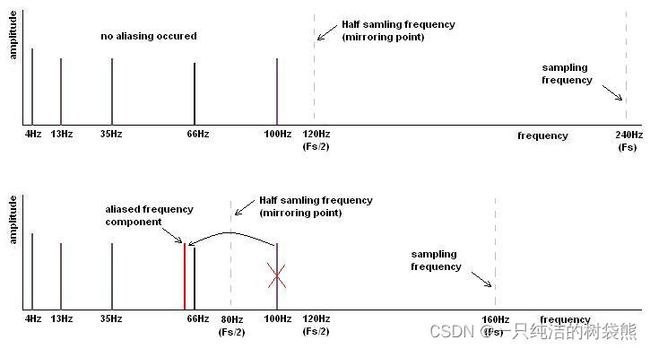
首先我们需要知道Nyquist-Shanon sampling theorem，即采样的频率需要至少是被采样信号最高频率的2倍，否则会在采样过程中出现一些错误，这样的错误被称为Aliasing（不太知道怎么翻译），即当采样频率为Fs时，如果信号有大于Fs/2的组分，就会相对于Fs/2对称翻折，例如下面这个例子

当采样频率Fs是160Hz，也即Fs/2为80Hz时，当信号中有100Hz的组分，会相对于80Hz进行翻折，变为一个60Hz的组分，导致采样出错。

知道了这样一个信号与系统之中的基础原理之后，我们就可以更进一步，开始对噪声进行一些基础的分析。

首先要提及的概念是白噪声，White Noise。白噪声是一种完全随机的噪声，它频率组分的幅度与频率无关（至少在会用到的频率范围内是这样的，热噪声好像几百GHz之后会下降）。那么当我们对这个噪声进行采样时，超出采样频率一半的频率组分会被Aliasing到 0-Fs/2 的范围内，与同频率的信号叠加，使得频率组分的幅度增加，虽然对于噪声不存在错误的说法，但是这样的现象依然会给我们带来困扰——因为信号的频率组分幅度是没有在采样过程中发生变化的，当噪声的幅度增加时，就会必然导致整个系统的SNR下降，造成采样的不理想。

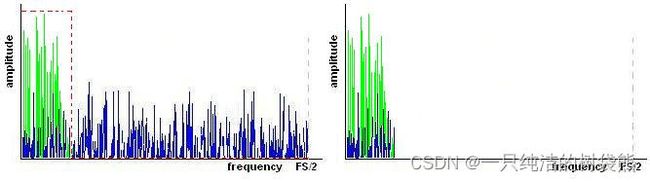
那么如何解决上述的问题呢？答案就是Oversampling，如下图所示

这个过程就和摊大饼差不多，你一勺的面糊一共就那么多，锅越大这个饼就越薄，当你在上面放上果篦儿的时候，果篦儿的厚度是一定的，当摊出来的饼越薄，你的这个果篦儿的厚度就更加显著，仔细想想，煎饼果子里的果篦儿和手抓饼里的果篦儿吃起来产生的感受都不太一样。在Oversampling之中，我们要的是信噪比SNR，也就是在前面这个例子中我们更希望突出果篦儿，那么只要搞口大的烙饼鏊子，即我们把 Fs/2 的数值拉到足够大，就可以把噪声摊到一个比较理想的厚度，得到一个满足要求的SNR（当然这其中又充满着Trade-off），就像下图这样

最后加个低通滤波就搞定了。因为是Delta-Sigma ADC，所以一般转化后整个数字滤波器解决这个问题。

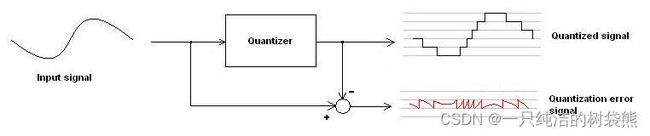
说了这么多，终于要讲到噪声整形了。既然我们看的是ADC，那么就一定存在一个数字和模拟交界的位置，完成这个转化的模块我们会将其称为Quantizer。可以想象一下，ADC的一个指标就是我这个ADC可以产生一个多少位的数字信号，位数越高，那么我们的数字信号就能更准确的反映模拟信号现在的状态。但是数字信号毕竟是离散的，而模拟信号是连续的，在这个量化的过程中一定会产生一定的误差，这个误差，即噪声，我们一般称之为Quantization noise。在表示的过程中，我们可以如下图所示，将一个信号表示为量化信号和量化噪声信号。

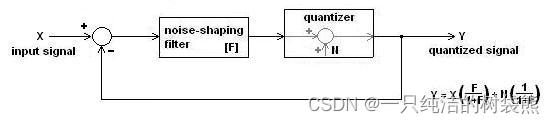
那我们知道了量化噪声怎么来的了，那么自然而然就会产生一个问题，我们前面通过提高采样频率可以在模拟端解决掉一些系统固有的输入端的噪声，但是这都到最后一步了，下一步就已经是数字信号了，这个时候引入噪声可怎么办啊？哎，这就需要用到Noise Shaping了，通过一些学的不太好的信号与系统的知识，咱这一条路走到头看着不太行，那就整个反馈嘛（当然也可以加点前馈，不过那就是更高阶的了），然后就可以随手（x）整出来一个这样的电路

你现在也先别管怎么想的，反正我们就搞出来这么一个传输函数
$$Y=X\left(\frac{F}{1+F}\right)+N\left(\frac{1}{1+F}\right)$$
分析一下，X是输入信号，N是量化噪声，在中间再搞传输函数是F的滤波器（很多是直接搞个运放），就形成了一个对于输入信号基本没有影响，但是对于量化噪声高通滤波的传输函数；这是非常理想的，因为信号主要在低频的部分，将低频的噪声通过这个高通滤波减弱后，再搞个低通滤波滤掉输入信号频率之外的组分，就可以得到一个很好的SNR，正如下图所示

这就是我们说的噪声整形（Noise Shaping），按照我个人的理解，这个过程的本质就是通过一系列前馈/反馈来形成对量化噪声有抑制作用的传输函数，以达到提高信噪比的效果。

Dynamic Amplifier，动态运放

动态运放的范围可太大了，我们这里指的主要是阅读的这篇文章中提到的动态运放FIA（Floating Inverter Amplifier），以及同作者曾经发表过的有关FIA的paper。这里的介绍过程就先沿着一篇专门介绍FIA的JSSC来说，参考的文章为[4]。

ps：需要注意的是，这里只是简单的列一下我自己理解下的进化过程，不会很严谨的写某种结构的增益、噪声、建立时间以及共模工作点等一系列参数的优缺点，需要理解的话建议自己去看。

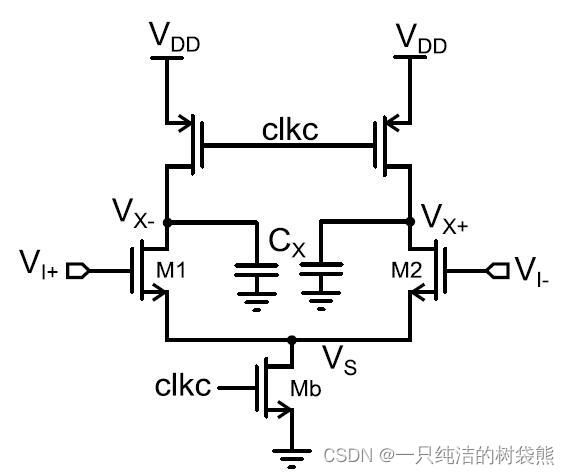
SA Latch

该结构就是一个通过时钟控制的动态运放。在clkc为0的时候通过pmos给Cx充电，在clkc为1的时候尾电流源的管子导通，Cx上的电荷通过两个输入管流向地。这个结构有个比较明显的问题，就是放点时候没个把门的，clkc一旦变成1就一泻千里了，这样就会导致功耗很大；但是在功耗很大的同时，这个结构在正经工作区的时间又不太长，当
$$V_{\text{x}+}/V_{\text{x}-}<V_{\mathrm{D}\mathrm{D}}-V_{\mathrm{T}\mathrm{H}\mathrm{N}}$$
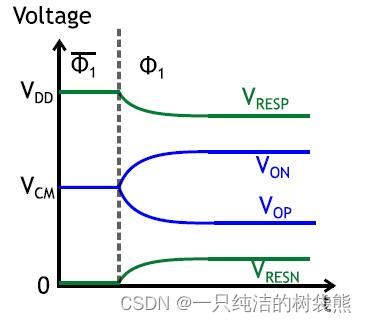
输入Nmos管就不在饱和区了，导致该运放失去了意义。正负输出点的电压变化曲线如下图所示

从这张图中不仅能看出来上面说的问题，还会发现当两边的Nmos管发生失配的时候放大的倍数区别还是会比较大。

那么我们不是就不想让他一次把电放完嘛，需要尾电流源这个位置有个把门的，那自然也就有了下述结构。

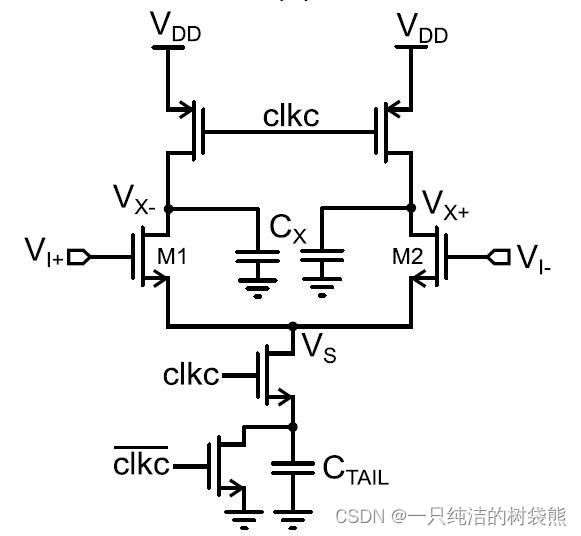
DB Integration

于是在这种结构中，当clkc为1的时候，Cx的放电不是无限制的，而是向尾部的C_Tail放一会儿电，直到M1和M2被关断就停止放电；而当clkc为0的时候，电源为Cx补充电荷，下端的Nmos管释放掉C_Tail上的电荷。

这种结构有两个好处，一个是降低了功耗，因为Cx比较大，所以如果不是一次性将其上的电荷全部放完，就会大大减小能量的损耗；第二个是，因为此种结构提供了更高的
$$g_m/I_D$$
这就提供了更大的增益和更低的输入参考噪声。

CMOS DB Integration Pre-Amplifier

为了进一步降低功耗，将上下都加上了电容用于储存电荷（具体怎么降就不说了）；此外由于这种结构使用了同时输入到Nmos和Pmos的结构，有
$$G_m\equiv g_{m,n}+g_{m,p}$$
提高了跨导，这就提供了更大的增益和更低的输入参考噪声。

但是使用上下两个电容会存在一个问题，就是无法保证上下尾电容上的电流相同，即在同一条支路上无法保证流过Pmos的电流和Nmos的电流相同：

在TT的情况下可以保证电流大小基本相同，但是在SF（Nmos：Slow | Pmos：Fast）的Corner下，流过Pmos的电流大于Nmos，输出点的电位被拉向电源，导致工作点出现错误；同样的，在FS的Corner下，Nmos电流大于Pmos，输出点的点位被拉向地。

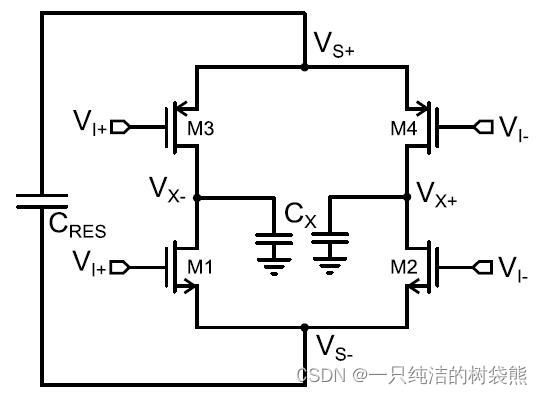
Floating Inverter Pre-Amplifier With Reservoir Capacitor

那两个电容上的电流大小不一样怎么办？那就给他整成一个嘛，这样你想不一样都不行了！

在一个比较理想的情况下，流过Nmos和Pmos的电流相等，那么Cx上的电流为0，只考虑共模的情况下，输出点的共模电平维持在一个恒定的值，可以不用加CMFB（共模反馈）电路，极大地简化了电路，降低了功耗；在存在小信号的情况下，其电平变化的情况如下图

至此应用于电路的FIA就介绍完了，后续另一篇文章中会有一些更有趣的变体，到时候再说。

文章主体

前面铺垫了这么多，终于可以进入到文章主体的部分了！

我们知道了什么是SAR ADC，前面介绍了什么是NS（Nintendo Switch（x）），那么什么是NS SAR ADC呢？我们可以先来看看作者在Introduction部分介绍的结构图

可以看出，由于是SAR ADC，其相比于Delta-Sigma会需要多一个DAC，用于将输出与输入进行比较；其余的Loop Filter和Quantizer部分和前文一致，本质上就是形成了一个传输函数，用于降低量化噪声。进一步细化，具体在电路中需要添加怎么样的结构，形成怎么样的传输函数：

这一坨前馈和反馈的东西我就不在这儿算了，其实Xiyuan Tang老师还有一篇三作是专门介绍NS SAR ADC的这些前馈、反馈是怎么考虑和怎么计算的，这里建议大家有兴趣的话直接去看[5]。

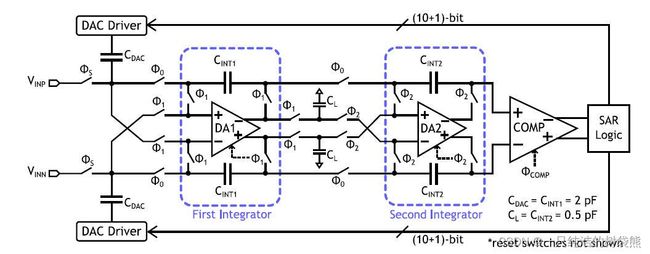
于是结构顶层的设计图为

${\varphi }_0$时刻主要是进行一般的SAR ADC的拟合，${\varphi }_1$时刻进行第一级的积分，结果储存在$C_{\text{INT1 }}$上，${\varphi }_2$时刻进行第二级的积分，结果储存在$C_{\text{INT2 }}$上。

比较器部分

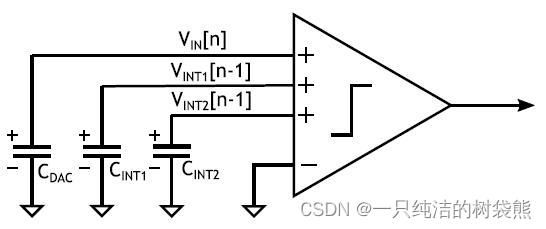
接下来进行细化分析，首先我们从信号的传输框图上发现输出端需要将${\varphi }_0$时刻拟合的结果和${\varphi }_1$、${\varphi }_2$时刻对余量的积分相加。在本设计中，作者很巧妙地将三个结果放在了同一条支路上，可以在需要的时刻直接读取三个电容（$C_{\text{INT1 }}$、$C_{\text{INT2 }}$、$C_{\text{DAC }}$）的数值之和，将其输入到比较器的输入端

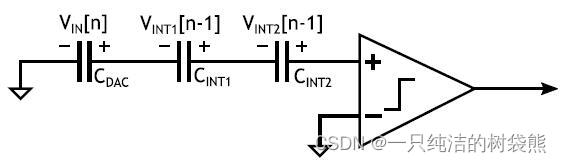
然而在一般的结构之中，SAR ADC的迭代过程与后面两次的余量积分（Residue Integration）相互独立，因此需要一个有三个输入端的比较器

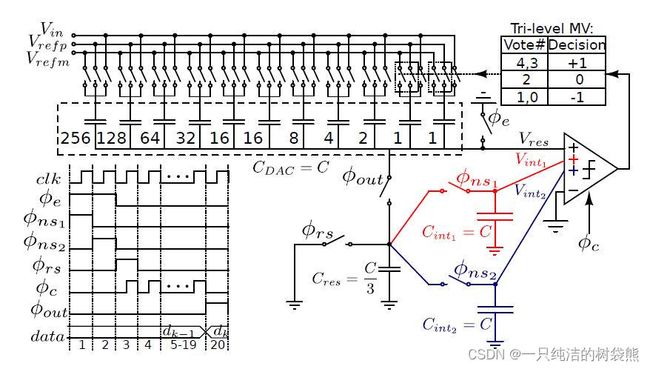
正如寄存器组或者多口SRAM，对于同类型的内容，端口越多其所占据的面积和功耗就越大，因此这后一种结构在这些因素之上是不如前一种的，当然后一种结构也在不断地有一些创新的设计，下图也是Nan Sun老师组的学生的Paper的结构 [6]

过程采用了电荷分配的积分方案，因此需要使用三个比较器的输入端口；为了简化设计，没有在比较器之外对余量进行放大，而是选择了使用三个输入端宽长比不同的比较器来进行放大

这样的设计同样也是非常巧妙的，很有趣。

FIA部分

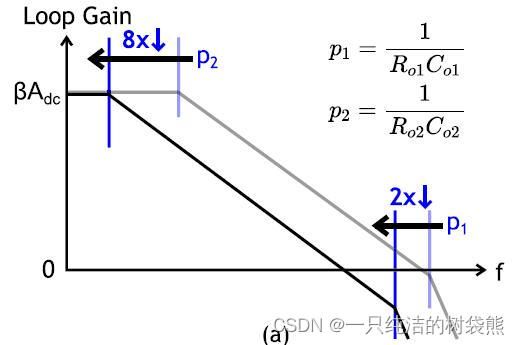
在电路图之中的DA（Dynamic Amplifier）是由两个串联的前文提到的FIA构成的，对输入信号进行两级的放大，并且保证相位不发生改变。此结构还在BW、PM上有着一些优势：当提高中间级的电阻时，主极点的内移速度远快于次极点的，可以形成很大的PM。

详细的参见原文。

冗余SAR DAC

为了防止对CDAC不太了解，这边先贴一篇文章介绍一下这种SAR ADC的基本原理 [7]。

可以看到电路的框图之中输出对DAC的反馈回路上写着**（10+1）bit** ，这个10是ADC的拟合位数的我们是知道的，那么这个1是什么意思呢？可以看到原文中有

The SAR core adopts a 10-bit CDAC with 1-bit redundancy.

在搜索这个Redundancy的过程中，我甚至找到了一篇唐鹤老师的学生的硕士毕业论文，那就引用这个了 [8]。

总的来说，冗余算法就是用来解决量化过程中出现的错误的，如下图

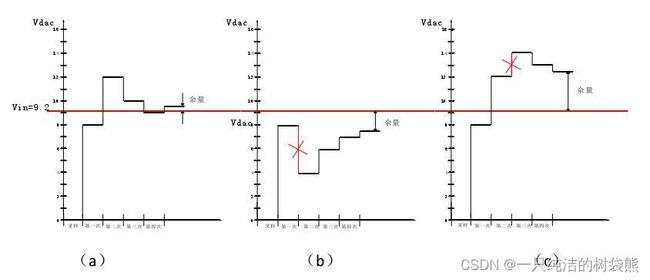
从后两张图可以看出，当前一级的的权重永远是后一级的两倍的时候，不论是第二次还是第三次量化的过程中出现了错误，都会导致无法挽回的错误，使得最后的余量远远超过理想的范围。

冗余算法则可以在量化过程中某一位的结果出现错误的时候对结果进行纠正，按照文章中的分类，其可以分为以下的三类：

• Sub-Radix 2：降低权重因子（这种方案在另一篇文章中有用到）
• 冗余位：在二进制权重的电容阵列之中插入额外的判断位，这个判断位和相邻位置的权重相同
• 不采用固定的权重因子，只要保证平均的权重小于2即可

其实不管怎么说，都是采用了平均值小于2的权重因子，让系统出现的判断错误存在挽回的余地，不至于一次出错就没得救了。如果将权重由[8 4 2 1 1]改变为[8 2 2 2 1]，那么量化出错的补救过程如下

可见不论哪一步出错都可以被补救回来，这就是冗余位的作用。仔细看看，其实[6]中的CDAC阵列也采用了冗余位。当然你要过大的位数错了，估计也没救了。

总结

前面刚刚开始看的时候一脸懵逼，查了很多资料之后，慢慢觉得这个设计之中真的有很多巧妙的构思，感叹模拟电路的美。

后面还有篇ISSCC，当然很多重点的东西已经在这里了，欢迎继续看下去嘿嘿。

顺便，在看了他们实验室的很多文章之后，真的很感慨科研是真的具有很强的传承性啊（手动狗头）。

参考文献

[1] Xiyuan Tang，A 13.5-ENOB, 107-μW Noise-Shaping SAR ADC With PVT-Robust Closed-Loop Dynamic Amplifier

[2] CSDN博客，模拟转数字电路中测量参数解析：SNR、SINAD、ENOB

[3] 个人网站，Delta-Sigma analog-to-digital converter

[4] Xiyuan Tang，An Energy-Efficient Comparator With Dynamic Floating Inverter Amplifier

[5] Jie Lu，An Overview of Noise-Shaping SAR ADC: From Fundamentals to the Frontier

[6] Haoyu Zhuang，A Second-Order Noise-Shaping SAR ADC with Passive Integrator and Tri-Level Voting

[7] Jason，知乎专栏

[8] 何生生，一种采用冗余位技术的12位SAR ADC的设计与研究