准备好了吗?蒋宝藏带你详解判别分析!
文章目录
- **前言**
- **一、5种软件介绍**
-
- **1.1 MATLAB**
- **1.2 Python**
- **1.2 SPSS**
- **1.4 Minitab**
- **1.4 Unscrambler**
- **二、判别分析算法案例——5种软件的具体操作**
-
- **2.1 MATLAB操作**
- **2.2 Python操作**
- **2.3 SPSS操作**
- **2.4 Minitab操作**
- **2.5 Unscrambler操作**
- **三、总结 —— 5种软件比较表格**
- **附录**
前言
在现如今大数据爆发的时代,数据分析软件应运而生,常见的数据分析软件有MATLAB、Python、SPSS、Minitab和Unscrambler。今天蒋宝藏就带你逐个认识一下这5款软件,并以我们常用的判别分析算法案例来比较这5款软件的优缺点!
小马扎准备好了吗???蒋宝藏课堂又开课啦!!!
一、5种软件介绍
1.1 MATLAB
MATLAB是美国MathWorks公司出品的跨平台商业数学软件,有Windows、MacOS、Linux版本,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。每年更新两个版本,上半年为a,下半年为b。
MATLAB是matrix&laboratory两个词的组合,意为矩阵实验室,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案。
它的基本单位是矩阵,几乎可以完成一切工程上的问题,但是需要用户有一定的编程基础,而且不开源。
1.2 Python
与MATLAB一样,Python也是一种跨平台的计算机程序设计语言。Python是一种面向对象的动态类型语言,最初被设计用于编写自动化脚本(shell),随着版本的不断更新和语言新功能的添加,越多被用于独立的、大型项目的开发。
Python一个很大的优势是开源,用户可以通过python实现很多人无法实现的功能。Python可以用于Web开发、科学计算和统计、人工智能、教育、桌面界面开发、软件开发、后端开发和网络爬虫等领域。
Python需要用户有扎实的编程基础,且由于是解释型语言,编译时速度没有C/C++快。
1.2 SPSS
SPSS为IBM公司推出的一系列用于统计学分析运算、数据挖掘、预测分析和决策支持任务的软件,有Windows和MacOS版本,应用于自然科学、技术科学、社会科学的各个领域。
SPSS的一个很重要的特点是操作界面友好,输出结果美观漂亮。用户不需要掌握编程知识,只要掌握一定的Windows操作技能,精通统计分析原理,就可以很轻松的入门操作这款软件。
SPSS的底层是由JAVA书写的,运行速度要比python快一些,但是不开源。
1.4 Minitab
与上述软件不同的是,Minitab除了数据分析功能,更是一款现代质量管理控制统计软件,是为质量改善、教育和研究应用领域提供统计软件、试验设计和服务的先导。
Minitab具有丰富的数据类算法,同时带有DOE(试验设计)功能,用户不需要编程知识也能熟练的玩转Minitab。
1.4 Unscrambler
Unscrambler 是一款在多变量分析(multivariate analysis, MVA)和实验设计软体领域深耕30多年的标竿专业分析软件,是全球数据分析和统计专业,研究人员和工程师的首选分析工具,可以利用软件多变量分析的强大功能,快速、轻松、准确地分析巨量和复杂的数据。
近30年来,Unscrambler为许多行业和组织提供支持,通过更深入的数据洞察,提高产品开发效率、加强对流程的理解和更好的产品质量控制。
Unscrambler不需要用户有专业的编程基础,只需会基础的数据算法基础就可以入门。与Minitab相同,Unscrambler配套的Design Export是专业的质量控制软件,为很多企业提供了质量管理技术。
Unscrambler开放了现在市面上大部分的数据接口,支持txt、excel、csv、mat等数据格式。最新版本的Unscrambler11开放了python接口,使得原来不支持的机器学习算法可以借助python来实现。
二、判别分析算法案例——5种软件的具体操作
为了更好的比较5种软件的区别,我们用以下这个经典分类案例
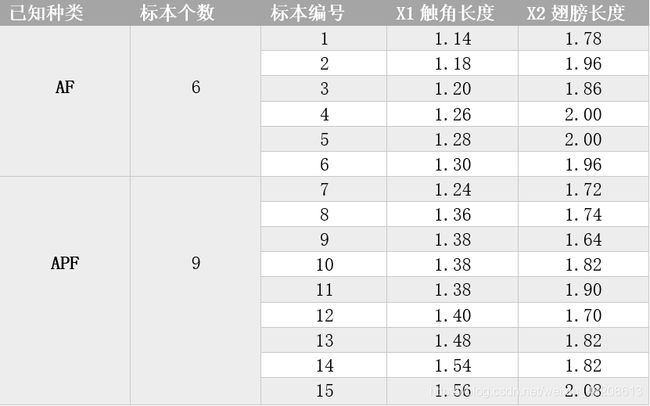
蠓的分类:
两种蠓虫AF和APF已由有关专家根据它们的触角长度和翅膀长加以区分,现有15只类型已知的蠓的标本,其中6只是AF蠓,9只是APF蠓,测得他们的触角长度和翅膀长数据如下:
另有3只类型未知的蠓的标本,触角长度和翅膀长度分别为: (1.24, 1.80), (1.28, 1.84), (1.40, 2.04)。
建立一种判别方法,能够根据这两种蠓的触角长度和翅膀长度,判别它们的种类。
这是一个典型的判别分析案例,下面我们分别用5种软件来实现这个案例。
2.1 MATLAB操作
在MATLAB中,解决这个问题,可以自己根据算法原理编程求解,也可用自带的判别分类函数classify来解决,在此我们用classify函数。
Classify函数的调用格式为:
[class,err] = classify(sample,training,group,type)
其中,sample为未知待分类的样本矩阵,training为已知分类的样本矩阵,它们有相同的列数,group为类别列向量,type为分类方法,缺省值linear(线性分类),还可以取quadratic(平方分类)、mahalanobis(马氏距离分类)。返回值class为样本的分类,err为分类误判率的值。
我们在MATLAB编辑器中输入以下代码:
clc
clear
training = xlsread('meng.xlsx','B2:C16');% 已知分类的矩阵
sample = xlsread('meng.xlsx','B17:C19'); %未知分类矩阵
group = [ones(6,1);2*ones(9,1)]; % 分类组别: 1为AF,2为APF
[class,err] = classify(sample,training,group)
便可以得到答案:
class =
1
1
1
err =
0
新的三类蠓都是APF类,且误判率为0.
MATLAB操作截图如图:
2.2 Python操作
在python中,没有自带的判别分析的函数,需要我们根据算法原理来书写程序。
我们在python编辑器pycharm中写入以下程序,截图如下(由于程序较多,放附录):
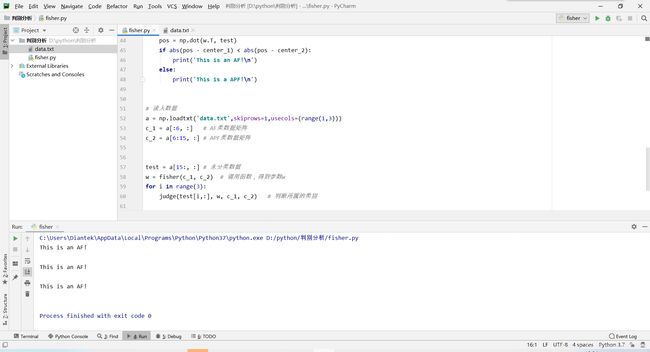
我们可以发现结果也是3个都是AF,与MATLAB结果相同。与MATLAB相比,虽然Python开源,但很多函数是缺失的,需要有扎实的编程基础。
2.3 SPSS操作
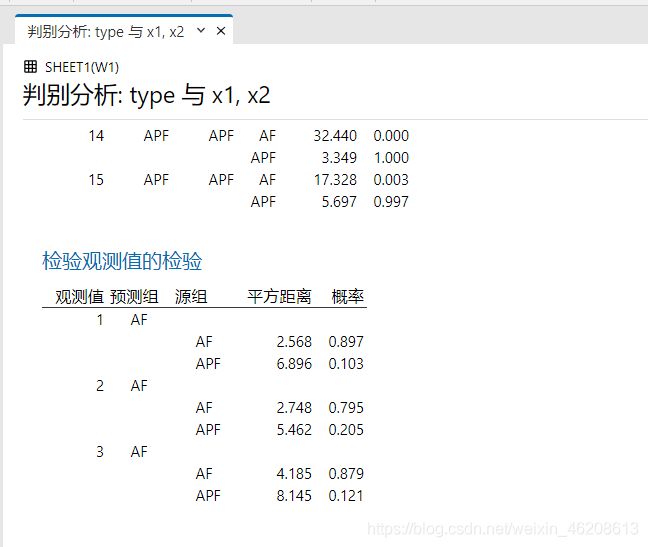
1.在SPSS中,集成了判别分析的功能,我们先打开SPSS,导入数据集meng_shu.xlsx.
3.转到分析 - 分类 - 判别式
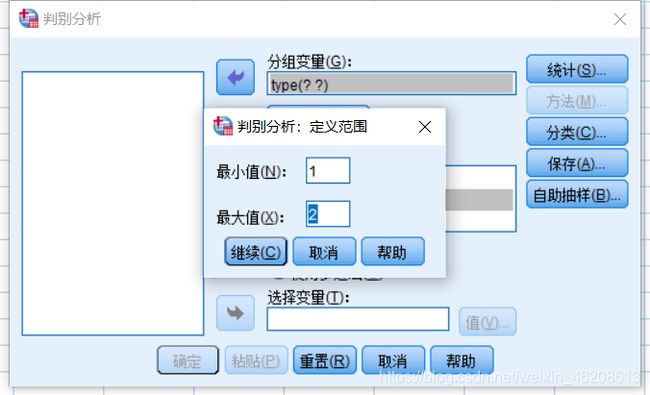
4.分组变量选择type,自变量选择x1和x2;分组变量定义范围最小值1,最大值2。
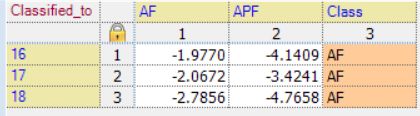
5.点击统计,函数关系选择费希尔和未标准化(因为x1和x2并无太大差异)。分类中选择个案结果。保存选上所有。最后点击确定。



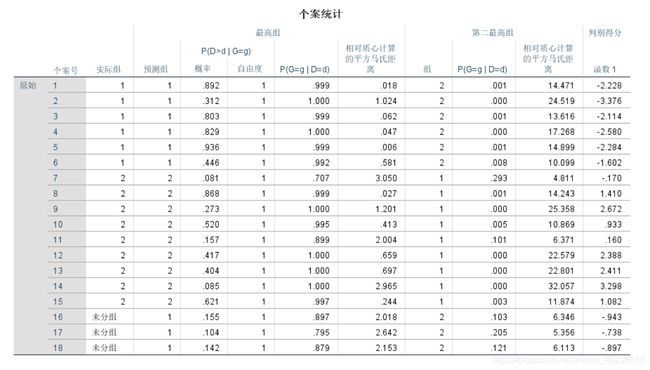
6.我们在输出文档的个案统计中观察发现:新的3个蠓的样本都属于1类,即AF类。同时,我们在数据编辑器中的Dis_1也可以看到都是属于1类。
2.4 Minitab操作
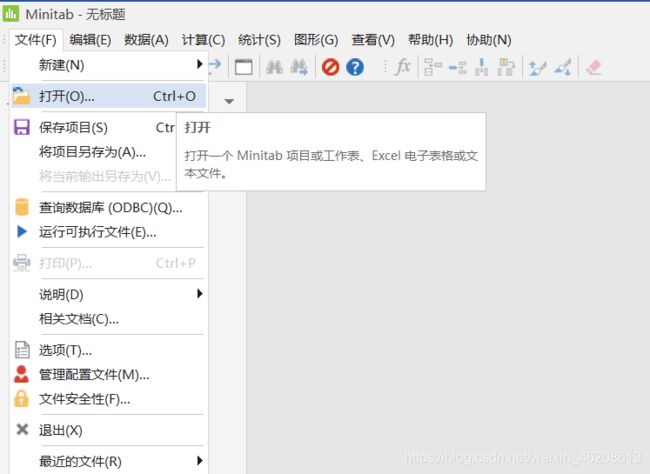
1.打开Minitab,文件-打开,导入meng.xlsx数据文件。

3.导入后,把3个待分类的样本数据复制粘贴到新的两列,命名为x和y。
4.转到统计 - 多变量 - 判别分析。
5.组选择type,预测变量选择x1和x2,判别函数选择线性。点击选项,预测组成员选择x和y,结果显示选择最后一个,点击确定。


6.我们在结果中,可以清晰的看到各项参数指标,以及最后3个样本的分类结果,都为AF类。
2.5 Unscrambler操作
1.导入meng.xlsx数据文件,选中已经分类的数据,并改名为classed
2.把type一列改为change data type-category


3. 再把未分类的蠓的数据导入,并改名为toclass

4. 为了更好的分析操作,我们把classed中的数据拆分为x1x2和type两段。
5. 接下来开始进行LDA,点击Task-Analyze-LDA,并做好如下设置:
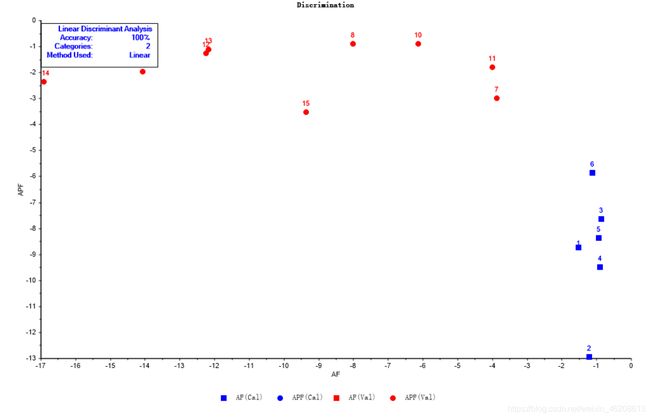
Predictors列选择x1x2,classification列选择type,点击ok


6.发现结果图分类的比较好,准确率百分之百。
6. 接下来开始预测,点击Task-Predict-Classification-LDA,并做下图设置:
三、总结 —— 5种软件比较表格
通过上述蠓的判别分析案例,我总结了以下表格:
附录
Python蠓的分类程序:
import numpy as np
def cov_and_avg(samples):
"""
给定一个类别的数据,计算协方差矩阵和平均向量
sample:一个类别样本的数据
return:2个值,协方差矩阵和平均向量
"""
u1 = np.mean(samples, axis=0)
col = samples.shape[1] # 样本数据的种类,即列数
cov_m = np.zeros((col, col))
for s in samples:
t = s - u1
cov_m += t * t.reshape(col, 1)
return cov_m, u1
def fisher(c_1, c_2):
"""
fisher算法实现
c_1:类别1的样本数据
c_2:类别2的样本数据
return:判别函数的系数
"""
cov_1, u1 = cov_and_avg(c_1)
cov_2, u2 = cov_and_avg(c_2)
s_w = cov_1 + cov_2
u, s, v = np.linalg.svd(s_w) # 奇异值分解
s_w_inv = np.dot(np.dot(v.T, np.linalg.inv(np.diag(s))), u.T)
return np.dot(s_w_inv, u1 - u2)
def judge(test, w, c_1, c_2):
"""
test:测试样本
w:fisher判别算法求得的系数
c_1:类别1的数据
c_2:类别2的数据
return:返回属于的类
"""
u1 = np.mean(c_1, axis=0)
u2 = np.mean(c_2, axis=0)
center_1 = np.dot(w.T, u1)
center_2 = np.dot(w.T, u2)
pos = np.dot(w.T, test)
if abs(pos - center_1) < abs(pos - center_2):
print('This is an AF!\n')
else:
print('This is a APF!\n')
# 读入数据
a = np.loadtxt('data.txt',skiprows=1,usecols=(range(1,3)))
c_1 = a[:6, :] # AF类数据矩阵
c_2 = a[6:15, :] # APF类数据矩阵
test = a[15:, :] # 未分类数据
w = fisher(c_1, c_2) # 调用函数,得到参数w
for i in range(3):
judge(test[i,:], w, c_1, c_2) # 判断所属的类别