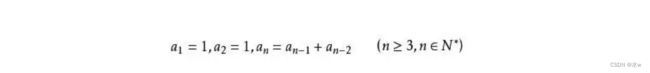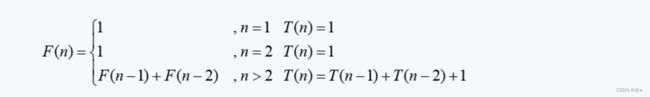【算法】妙不可言---算法复杂性
#14天阅读挑战赛#
14天阅读挑战赛
CSDN近期举办14天阅读打卡活动
目录
一、算法复杂性
◼ 一棋盘粮有多少
◼ 神奇的兔子数列
一、算法复杂性
如果我们想要求这样一个序列的每个元素之和:
你打算怎么求这个序列之和?我们一般首先的想法就是遍历一遍,第一个是-1,第二个是1,那么这样依次for遍历,进行求和。
我们还可以发现第一个是-1,第二个是1,那么每两个元素之和正好是0。我们可以根据序列的这个性质来进行快捷求和。
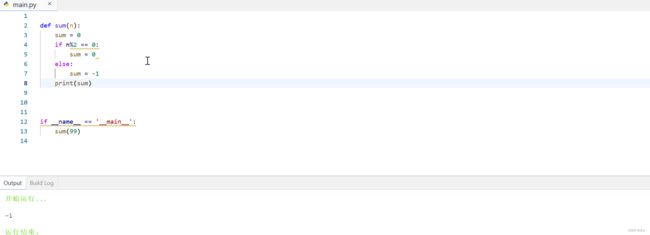
def sum(n):
sum = 0
if n%2 == 0:
sum = 0
else:
sum = -1
print(sum)
if __name__ == '__main__':
sum(99)
那么这个例子当中,我们实现对序列求和的方法,也可以称之为一个算法。
一个算法应该具有以下五个重要的特征:
1、有穷性(Finiteness),算法必须能在执行有限个步骤之后终止;
2、确切性(Definiteness),算法的每一步骤必须有确切的定义;
3、输入项(Input),一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输入是指算法本身定出了初始条件;
4、输出项(Output),一个算法有一个或多个输出,以反映对输入数据加工后的结果。没有输出的算法是毫无意义的;
5、可行性(Effectiveness),每个计算步骤都可以在有限时间内完成。算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步骤,即每个计算步骤都可以在有限时间内完成。
那我们怎么知道一个算法好不好呢?应该从哪些方面对算法进行评估呢?
算法优劣的五个标准是什么:
1、时间复杂度:它定量描述了该算法的运行时间,即计算程序运行的时间,空间复杂度, 就是所占的内存空间。
2、空间复杂度:是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了,因为每次递归都要存储返回信息。
3、稳定性:不会因为输入的不同而导致不稳定的情况发生;
4、算法思路是否简单:越简单越容易实现越好;
5、渐近时间复杂度:是指当问题规模趋向无穷大时,该算法时间复杂度的数量级。
一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。
同一问题可用不同算法解决,而一个算法的质量优劣将影响到算法乃至程序的效率。算法分析的目的在于选择合适算法和改进算法。
◼ 一棋盘粮有多少
传说西塔发明了国际象棋而使国王十分高兴,他决定要重赏西塔,西塔说:“我不要你的重赏 ,陛下,只要你在我的棋盘上赏一些麦子就行了.在棋盘的第1个格子里放1粒,在第2个格子里放2粒,在第3个格子里放4粒,在第4个格子里放8粒,依此类推,以后每一个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到放满第64个格子就行了”.区区小数,几粒麦子,这有何难,“来人”,国王令人如数付给西塔。
计数麦粒的工作开始了,第一格内放1粒,第二格内放2粒第三格内放2’粒,…还没有到第二十格,一袋麦子已经空了.一袋又一袋的麦子被扛到国王面前来.但是,麦粒数一格接一格飞快增长着,国王很快就看出,即便拿出全国的粮食,也兑现不了他对西塔的诺言。
原来,所需麦粒总数为:2的64次方减1 =18446744073709551615
这些麦子究竟有多少?打个比方,如果造一个仓库来放这些麦子,仓库高4公尺,宽10公尺,那么仓库的长度就等于地球到太阳的距离的两倍.而要生产这么多的麦子,全世界要两千年.尽管国家非常富有,但要这样多的麦子他是怎么也拿不出来的.这么一来,国王就欠了西塔好大一笔债。
那么我们可以用那些方法得到所需麦粒总数呢?
(1)把棋盘上的64个格子需要放的麦粒数量加起来为S,那么,
(2)等式两边同时乘以2,
(3)用等式2减去等式1,我们就可以得到所需麦粒总数为:2的64次方减1
![]()
由指数函数图象来看,简直可以说是直线增长的,比爆炸的威力还要大。我们称这样的函数为爆炸增量函数。指数函数又叫爆炸函数,指数爆炸,时间复杂度是指数阶,是指指数函数在符合一定的条件时,将出现“爆炸性”增长。
我们经常见到有些算法在调试的时候是没报错的,运行一段时间也没问题,但是在关键时刻计算机会宕机。因此,在程序设计中我们应该避免这样的复杂度。
宕机:宕机,就是我们大家日常见到的电脑死机。在计算机中,我们用dowm来表示把机器停止,转换成汉字就是宕机,服务器不能正常工作了,其中也包括一切服务器出现死机的原因。
最常见的五种时间复杂度:
- O(1):常数复杂度, 最快的算法。
- 例如取数组第1000000个元素,字典和集合的存取都是O(1), 数组的存取是O(1)O(logN)
- O(logN):对数复杂度。假设有一个有序数组, 以二分法查找,时间复杂度为O(logN)。
- O(n):线性复杂度。假设有一个数组, 以遍历的方式在其中查找元素。
- O(nlogn):求两个数组的交集, 其中一个是有序数组。 A数组每一个元素都要在B数组中进行查找操作,每次查找如果使用二分法则复杂度是 logN。
- O(n2):平方复杂度。求两个无序数组的交集。
◼ 神奇的兔子数列
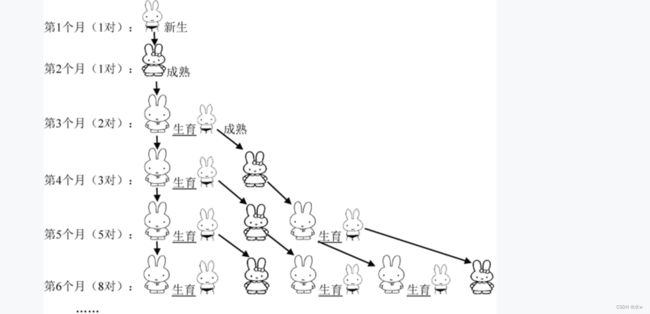
意大利中世纪数学家斐波那契以兔子繁殖为例子引入一个数列,称为“兔子数列”。
假设兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
我们拿新出生的一对小兔子分析一下:
第一个月小兔子没有繁殖能力,所以还是一对。两个月后,生下一对小兔对数共有两对。三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,所以一共是三对。
依次类推可以列出下表:
可以看出总体对数构成了一个数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,……
a = b =1
第一个月 1对 莫名其妙得到的(别死磕总之就是有兔子了)
第二个月 1对 长大了(下个月可以生兔子了)
第三个月 2对 第一个月的可以生兔子了——————第一月生了小兔子所以有2对
第四个月 3对 第三个月生的这个月在长大 ————最开始的又生了一对兔子 所以你有三个
第五个月 5对 第三个月生的可以生兔子了————第四个月的在长大———— 也就是这个月你有两只兔子生了小兔子 所以你有只兔子
第六个月 8对 第四个月生的可以生兔子了————第五个月的在长大 ———— 也就是这个月你有三只兔子生了小兔子 所以你有只兔子
第七个月 12对 规律 下一项=前两项之和
第八个月 21对
第九个月 34对
第十个月 55对
第十一个月 89对
第十一个月 144对
for x in range(12-2): 前两个月不生兔子所以写死了a=b=1
c = a + b c为下一项吗 下一项为前两项和 所以c = a+b
a,b = b,c python特有的变量交换 a=1 b=2 a,b =b,a a=2 b=1
print(c)
这个数列从第3项开始,每一项都等于前两项之和。其通项公式可以表达为:
这个数列就是斐波那契数列,也叫黄金分割数列。
之所以称为黄金分割数列,是因为随着数列项数的增加,前一项与后一项之比越来越逼近黄金分割的数值0.6180339887……
1÷1=1,1÷2=0.5,2÷3=0.666,3÷5=0.6,5÷8=0.625,55÷89=0.617977,144÷233=0.618025……越到后面,这些比值越接近黄金比。
斐波那契数列中的斐波那契数在我们的生活中随处可见,比如植物花朵的花瓣数、蜂巢、蜻蜓翅膀、超越数e、黄金矩形、等角螺线、十二平均律等。
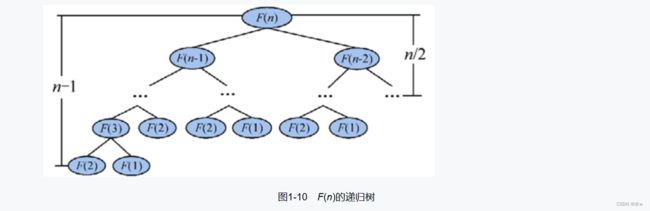
递归表达式如下,
那么,我们要怎么设计算法呢? 首先按照递归表达式简单设计一下个递归算法,
def Fibonacci(self, n):
#递归实现
# n=0 f(0)=0
if n==0:
return 0
# n=1 f(1)=1
if n==1:
return 1
#if n>1 f(n)=f(n-1)+f(n-2)
if n>1:
num=self.Fibonacci(n-1)+self.Fibonacci(n-2)
return num
return None
'''
这种方法简单易理解,但是不推荐,运行时间较长因此,递归表达式和时间复杂度的关系如下,
由于T(n)>=F(n),因此这是一个指数阶的算法,我们按照递归表达式简单设计的递归算法的时间复杂度是指数阶的,属于爆炸增量函数,这种方法虽然简单易理解,但是不推荐,运行时间较长。在程序设计中我们应该避免这样的复杂度。
我们看一下下面这种方法,既然斐波那契数列从第3项开始,每一项都等于前两项之和,那么如果我们记录前两项的值,进行求和,只需要运算一次加法就可以得到下一项的值了。
那么这样的话,时间复杂度会不会低一些呢?
def Fibonacci(self, n):
# n=0 f(0)=0
if n==0:
return 0
# n=1 f(1)=1
if n==1:
return 1
#if n>1 f(n)=f(n-1)+f(n-2)
a=1
b=0
#if n>1 f(n)=f(n-1)+f(n-2)
#h=a+b
#当 n=2 h=0+1
for i in range(0,n-1):
ret=a+b
b=a
a=ret
return ret
很明显,现在时间复杂度为O(n),从指数阶降到了多项式阶,算法效率有了重大的突破!