第一章-算法之美
第一章-算法之美
- 1.1打开算法之门
- 1.2 妙不可言——算法复杂性
- 1.3美不胜收——魔鬼序列
- 1.4灵魂之交——马克思手稿中的数学问题
- 1.5算法学习瓶颈
- 1.6你怕什么
1.1打开算法之门
数据结构 + 算法 = 程序
数据结构是程序的骨架,算法是程序的灵魂。
1.2 妙不可言——算法复杂性
一个序列之和的不同求法:
-1,1,-1,1,……,(-1)n
# 算法1-1
n = int(input())
sum_1 = 0
for i in range(1, n+1):
sum_1 += pow(-1, i)
print(sum_1)
# 算法1-2
n = int(input())
if n % 2 == 0:
sum_1 = 0
else:
sum_1 = -1
print(sum_1)
算法是指对特定问题求解步骤的一种描述。
算法具有以下特性:
(1) 有穷性:算法是由若干条指令组成的有穷序列,总是在执行若干次后结束,不可能永不停止。
(2) 确定性:每条语句有确定的含义,无歧义。
(3) 可行性:算法在当前环境条件下可以通过有限次运算实现。
(4) 输入输出:有零个或多个输入,一个或多个输出
"好"算法的标准:
(1) 正确性:正确性是指算法能够满足具体问题的需求,程序运行正常,无语法错误,能够通过典型的软件测试,达到预期的需求。
(2) 易读性:算法遵循标识符命名规则,简洁易懂,注释语句恰当适量,方便自己和他人阅读,便于后期调试和修改。
(3) 健壮性:算法对非法数据及操作有较好的反应和处理。例如,在学生信息管理系统中登记学生年龄时,若将21岁误输入为210岁,系统应该提示错误。
(4) 高效性:高效性是指算法运行效率高,即算法运行所消耗的时间短。算法时间复杂度就是算法运行需要的时间。现代计算机一秒钟能计算数亿次,因此不能用秒来具体计算算法消耗的时间,由于相同配置的计算机进行一次基本运算的时间是一定的,我们可以用算法基本运算的执行次数来衡量算法的效率。因此,将算法基本运算的执行次数作为时间复杂度的衡量标准。
(5) 低存储性:低存储性是指算法所需要的存储空间低。对于像手机、平板电脑这样的嵌入式设备,算法如果占用空间过大,则无法运行。算法占用的空间大小成为空间复杂度。
时间复杂度:算法运行需要的时间,一般将算法的执行次数作为时间复杂度的度量标准。
# 算法1-3
Sum = 0 # 运行1次
Total = 0 # 运行1次
for i in range(1, n+1): # 运行n次
Sum += i # 运行n次
for j in range(1, n+1): # 运行n*n次
Total += i*j # 运行n*n次
把算法的所有语句的运行次数加起来:1+1+n+n+n * n+n * n,可以用一个函数T(n)表示:T(n) = 2n2+2n+2
当n足够大时,可以看到算法运行时间主要取决于第一项,后面的甚至可以忽略不计。
算法1-3的时间复杂度渐近上限为O(f(n)) = O(n2) ----------->用到极限
我们通常使用时间复杂度渐近上限O(f(n))来表示时间复杂度
# 算法1-4
i = 1 # 运行1次
while i <= n: # 可假设运行x次
i *= 2 # 可假设运行x次
观察算法1-4,无法立即确定while及i2运行了多少次。这时可假设运行了x次,每次运算后i的值为21,22,23,…,2x,当i=n时结束,即2x=n时结束,则x=log2n,那么算法1-4的运算次数为1+2log2n,时间复杂度渐近上限为O(f(n)) = o(log2n)。
在算法解析中,渐近复杂度是对算法运行次数的粗略估计,大致反映问题规模增长趋势,而不必精确计算算法的运行时间。在计算渐近时间复杂度时,可以只考虑对算法运行时间贡献大的语句,而忽略那些运算次数少的语句,循环语句中处在循环内层的语句往往运行次数最多,即为对运行时间贡献最大的语句。例如在算法1-3中,Total = Total + i * j 是对算法贡献最大的语句,只计算该语句的运行次数即可。
注意: 不是每个算法都能直接计算运行次数的。
# 算法1-5
def findx(x): # 在列表中顺序查找x
list_chu = [i for i in range(1,100)]
for j in range(len(list_chu)):
if list_chu[j] == x:
return j # 返回其下标j
return -1
print(findx(50))
我们很难计算算法1-5中的程序到底执行了多少次,因为运行次数依赖于x在列表中的位置,如果第一个元素就是x,则执行1次(最好情况);如果最后一个元素是x,则执行n次(最坏情况);如果分布概率均等,则平均执行次数为(n + 1)/ 2。
有些算法,如排序、查找、插入等算法,可以分为最好、最坏和平均情况分别求算法渐近复杂度,但我们考查一个算法通常考查最快情况,而不是最好情况,最坏情况对衡量算法的好坏具有实际的意义
空间复杂度:算法占用的空间大小。一般将算法的辅助空间作为衡量空间复杂度的标准。
空间复杂度的本意是指算法在运行过程中占用了多少存储空间。算法占用的存储空间包括:
(1) 输入/输出数据;
(2) 算法本身;
(3) 额外需要的辅助空间。
输入/输出数据占用的空间是必须的,算法本身占用的空间可以通过精简算法来缩减,但这个压缩的量是很小的,可以忽略不计。而在运行时使用的辅助变了所占用的空间,即辅助空间是衡量空间复杂度的关键因素。
# 算法1-6
def change(x,y): # x与y交换
temp = x # temp为辅助空间
x = y
y = temp
return x,y
print(change(1,2))
该算法使用了一个辅助空间temp,空间复杂度为O(1)。
注意: 递归算法中,每一次递推需要一个栈空间来保存调用记录,因此,空间复杂度需要计算递归栈的辅助空间。
# 算法1-7
def jiecheng(n): # 计算n的阶乘
if n < 0: # 小于零的数无阶乘值
print("data error!")
elif n == 0 or n == 1:
return 1
else:
return n * jiecheng(n - 1)
print(jiecheng(4))
阶乘是典型的递归调用问题,递归包括递推和回归。递推是将原问题不断分解成子问题,直到达到结束条件,返回最近子问题的解;然后逆向逐一回归,最终达到递推开始的原问题,返回原问题的解。

图1-5和图1-6的递推、回归过程是我们从逻辑思维上推理,用图的方式形象地表达出来的,但计算机内部是怎么处理的呢?计算机使用一种称为"栈"的数据结构,它类似于一个放一摞盘子的容器,每次从顶端放进去一个,拿出来的时候只能从顶端拿一个,不允许从中间插入或抽取,因此称为"后进先出"(last in first out)。
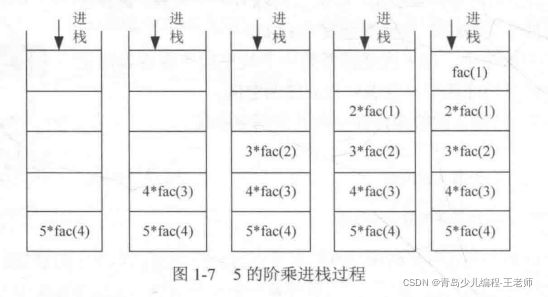

从图1-7和图1-8的进栈、出栈过程中,我们可以很清晰地看到,首先把子问题一步步地压进栈,直到得到返回值,再一步步地出栈,最终得到递归结果。再运算过程中,使用了n个栈空间作为辅助空间,因此阶乘递归算法的空间复杂度为O(n)。
1.3美不胜收——魔鬼序列
趣味故事1-1:一棋盘的麦子
有一个古老的传说,有一位国王的女儿不幸落水,水中游很多鳄鱼,国王情急之下下令:"谁能把公主就上来,就把女儿嫁给他。"很多人纷纷退让,一个勇敢的小伙子挺身而出,冒着生命危险把公主救了上来,国王一看是个穷小子,想要反悔,说:"除了女儿,你要什么都可以。"小伙子说:"好吧,我只要一棋盘的麦子。您在第一个格子里放1粒麦子,第二个格子里放2粒,第三个格子里放4粒,第四个格子里放8粒,以此类推,每个格子里的麦子粒数都是前一格的两倍。把这64个格子都放好了就行,我就要这么多。"国王听后哈哈大笑,觉得小伙子的要求很容易满足,满口答应。结果发现,把全国的麦子都拿来,也填不完这64格… …国王无奈,只好把女儿嫁给了这个小伙子。
# 方法1
def maizi():
Sum = 0
for i in range(64): # 共64格格子
Sum += 2 ** i # 第一个格子是1,每个格子是前一个格子的2倍
return Sum # 返回总数
print(maizi())
# 方法2:
Sum = 2 ** 64 - 1
print(Sum)

我们称这样的函数为爆炸增量函数(方法2,即图解方法),想一想,如果算法时间复杂度是O(2n)会怎样?随着n的增长,这个算法会不会"爆掉"?
注意: 宕机就是死机,指电脑不能正常工作了,包括一切原因导致的死机。计算机主机出现意外故障而死机,一些服务器(如数据库)死锁,服务器的某些服务停止运行都可以称为宕机。
常见的算法时间复杂度游以下几类:
(1) 常数阶
常数阶算法运行的次数是一个常数,如5、20、100。常数阶算法时间复杂度通常用O(1)表示,如算法1-6,它的运行次数为4,就是常数阶,用O(1)表示。
(2) 多项式阶
很多算法时间复杂度是多项式,通常用O(n)、O(n2)、O(n3)等表示。例如算法1-3就是多项式阶。
(3) 指数阶
指数阶时间复杂度运行效率极差,常见的有O(2n)、O(n!)、O(nn)等。使用这样的算法要慎重,如趣味故事1-1.
(4) 对数阶
对数阶时间复杂度运行效率较高,常见的有O(logn)、O(nlogn)等,如算法1-4。
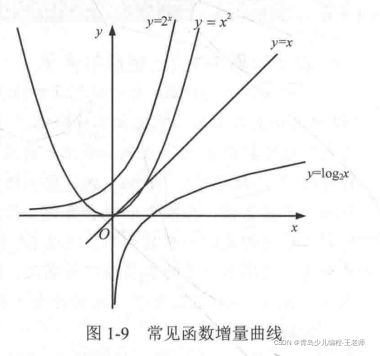
从图1-9中可以看出,指数阶增量随着x的增加而急剧增加,而对数阶增加缓慢。它们之间的关系为:
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
我们在设计算法时要注意算法复杂度增量的问题,尽量避免爆炸级增量。
趣味故事1-2:神奇兔子数列
假设第一个月有1对刚诞生的兔子,第二个月进入成熟期,第三个月开始生育兔子,而1对成熟的兔子每月会生1对兔子,兔子永不死去……那么,由1对初生兔子开始,12个月后会有多少对兔子呢?
(1) 问题分析
第1个月:新生
第2个月:成熟
第3个月:成熟+新生
第4个月:成熟+成熟+新生
第5个月:成熟+成熟+成熟+新生+新生
第6个月:成熟+成熟+成熟+成熟+成熟+新生+新生+新生
这个数列有个十分明显的特点,从第3个月开始,当月的兔子数=上月兔子数+当月新生兔子数,而当月新生兔子数正好是上上月的兔子数。因此,前面两项之和,构成了后一项,即:
当月的兔子数=上月兔子数+上上月的兔子数
斐波那契数列如下:
1,1,2,3,5,8,13,21,34,…
递归表达式:
F(n) = 1 , n=1
F(n) = 1 , n=2
F(n) = F(n-1) + F(n-2) , n>2
# 算法1-8
def tuzi(month):
if month < 1:
return -1
elif month == 1 or month == 2:
return 1
else:
return tuzi(month-1) + tuzi(month-2)
print(tuzi(0))
算法1-8是一个指数阶的算法!它的时间复杂度属于爆炸增量函数
# 算法1-9
def tuzi(month):
list_tuzi = []
if month < 1:
return -1
list_tuzi.append(1)
list_tuzi.append(1)
for i in range(2,month+1):
list_tuzi.append(list_tuzi[i-1] + list_tuzi[i-2])
return list_tuzi[month-1]
print(tuzi(12))
算法改进
既然斐波那契数列中的每一项是前两项之和,如果记录前两项的值,只需要一次加法运算就可以得到当前项,见算法1-9。
很明显,算法1-9的时间复杂度为O(n)。算法仍然是按照F(n)的定义,所以正确性没有问题,而时间复杂度却从算法1-8的指数阶降到了多项式阶。
# 算法1-10
def tuzi(month):
if month < 1:
return -1
if month == 1 or month == 2:
return 1
s1 = 1
s2 = 1
for i in range(2,month+1):
s2 = s1 + s2 # 辗转相加法
s1 = s2 - s1 # 记录前一项
return s1
print(tuzi(12))
算法1-9使用了一个辅助数组记录中间结果,空间复杂度也为O(n),其实我们只需要得到第n个斐波那契数,中间结果只是为了下一次使用,根本不需要记录。因此,我们采用迭代法进行算法设计,见算法1-10。
算法1-10使用了若干个辅助变量,迭代辗转相加,每次记录前一项,时间复杂度为O(n),但空间复杂度降到了O(1)。
问题的进一步讨论: 实质上,斐波那契数列时间复杂度还可以降到对数阶O(logn)
个人比较喜欢的一段话
斐波那契数列起源于兔子数列,这个现实中的例子让我们真切地感到数学源于生活,生活中我们需要不断地通过现象发现数学问题,而不是为了学习而学习。学习的目的是满足对世界的好奇心,如果我们怀着这样一颗好奇心,或许世界会因你而不同!斐波那契通过兔子繁殖来告诉我们这种数学问题的本质,随着数列项的增加,前一项与后一项之比越来越逼近黄金分割的数值0.618时,我彻底被震惊到了,因为数学可以表达美,这是令我们叹为观止的地方。当数学创造了更多的奇迹时,我们会发现数学本质上是可以回归到自然的,这样的事例让我们感受到数学的美,就像黄金分割、斐波那契数列,如同大自然中的一朵朵小花,散发着智慧的芳香……
1.4灵魂之交——马克思手稿中的数学问题
趣味故事1-3:马克思手稿中的数学问题
马克思手稿中有一道趣味数学问题:有30个人,其中有男人、女人和小孩,这些人在一家饭馆吃饭花了50先令;每个男人花3先令,每个女人花2先令,每个小孩花1先令;问男人、女人和小孩各有几人?
# 我的暴力解法
def tuzi(month):
if month < 1:
return -1
if month == 1 or month == 2:
return 1
s1 = 1
s2 = 1
for i in range(2,month+1):
s2 = s1 + s2 # 辗转相加法
s1 = s2 - s1 # 记录前一项
return s1
print(tuzi(12))
问题分析
由nan + nv + xiao = 30和3nan+2nv+xiao=50两式相减可得:2nan+nv=20
因为nan、nv为正整数,nan最大只能取9,所以nan变化范围是1-9。
# 算法1-11
for nan in range(1, 10):
nv = 20 - 2 * nan
xiao = 30 - nan - nv
if 3*nan + 2*nv + xiao == 50:
print(nan,nv,xiao)
算法分析
算法完全按照题中方程设计,因此正确性毋庸置疑。对算法时间复杂度贡献最大的语句是for nan in range(1, 10),该语句的执行次数是9,for循环中3条语句的执行次数也为9,其他语句执行次数为1,时间复杂度为O(1),没有使用辅助空间,空间复杂度也为O(1)。
问题的进一步讨论
为什么让nan来确定nv和xiao的值?让nv、xiao来确定行不行?有更好的算法降低时间复杂度吗?
趣味故事1-4:爱因斯坦的阶梯
爱因斯坦家里有一条长阶梯,若每步跨2阶,则最后剩1阶;若每步跨3阶,则最后剩2阶;若每步跨5阶,则最后剩4阶;若每步跨6阶,则最后剩5阶。只有每次跨7阶,最后才刚好1阶不剩。请问这条阶梯共有多少阶?
# 算法1-12
jie = 0
while True:
if jie%2==1 and jie%3==2 and jie%5==4 and jie%6==5 and jie%7==0:
print(jie)
break
else:
jie += 1
因为jie从1开始,找到第一个满足条件的数就停止,所以算法1-12中的while语句运行了119次。
# 算法1-13
jie = 7
while True:
if jie%2==1 and jie%3==2 and jie%5==4 and jie%6==5:
print(jie)
break
else:
jie += 7
算法改进
因为每次跨7阶,最后刚好1阶不剩,因此这个数一定是7的倍数。算法1-13为改进算法。该算法中while语句执行了119/7=17次。
趣味故事1-5:哥德巴赫猜想
哥德巴赫猜想:任一大于2的偶数,都可表示成两个素数之和。
验证:2000以内大于2的偶数都能够分解为两个素数之和。
# 质数又称素数。一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;
# 否则称为合数(规定1既不是质数也不是合数)。
# 算法1-14
def isprime(num): # 判断是否为素数
if num <= 1:
return 0
elif num == 2:
return 1
else:
for i in range(2, num//2+1):
if num % i == 0:
return 0
return 1
for j in range(2, 2001, 2): # 对2000以内大于2的偶数进行判断
for k in range(2, j+1): # 分解
if isprime(k) and isprime(j-k): # 如果分解后的数为素数
print(j, k, j-k)
break
算法改进——未完成代码
先判断所有分解可能得到的数是否为素数,然后把结果存储下来,有以下两种方法:
(1) 用布尔型数组flag[2…1998]记录分解可能得到的数(2-1998)所有数是不是素数,分解后的值作为下标,调用该数组即可。时间复杂度减少,但空间复杂度增加.
(2) 用数值型数组data[302]记录2~1998中所有的素数(302个)。
A、分解后的值,采用折半查找(素数数组为有序存储)的办法在素数数组中查找,找到就是素数,否则不是。
B、不分解,直接在素数数组中找两个素数之和是否为i,如果找到,验证成功。因为素数数组为有序存储,当两个数相加比i大时,不需要再判断后面的数。
1.5算法学习瓶颈
总结
(1) 无论做研究还是实际工作,一个计算机专业人士最重要的能力就是解决问题——解决那些不断从实际应用中冒出来的新问题
(2) 算法作为一门学问,有两条几乎平行的线索。一个是数据结构(数据对象):数、矩阵、集合、串、排列、图、表达式、分布等。另一个是算法策略:贪心、分治、动态规划、线性规划、搜索等。两者要结合着一起学。
1.6你怕什么
本章主要说明以下问题:
(1)将程序执行次数作为时间复杂度衡量标准。
(2)时间复杂度通常用渐近上界符号f(n)表示。
(3)衡量算法的好坏通常考查算法的最坏情况。
(4)空间复杂度只计算辅助空间。
(5)递归算法的空间复杂度要计算递归使用的栈空间。
(6)设计算法时尽量避免爆炸级增量复杂度。