基于蚂蚁-遗传优化算法的路径规划问题(Matlab代码实现)
欢迎来到本博客❤️❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码
1 概述
移动机器人路径规划技术,指的是机器人自身传感器对周围环境的感知,然后自主的规划出一条安全且高效的运行路径,同时完成相应的任务。目前移动机器人路径规划常用的算法有人工势场法、RRT算法、A*算法、Q学习法等,另外还有一些仿生类算法如粒子群算法、遗传算法、蚁群算法等。上述算法在机器人路径规划领域都有着良好表现,但是也存在一些问题,例如在进行路径规划时大多只关注路径的长度而忽视了其它因素,因此在实际应用场景中依旧存在较大问题。因为在移动机器人实际工作中,不仅力求路径尽可能短而且对转弯次数及高度变化等方面也有着较高要求。如果只考虑路程这个单一要素,可能将导致转弯次数增多、爬坡度次数多等不利情形,这不仅会使运行成本增加,还可能会对机器人寿命造成损害。因此,探索一种在综合指标表现最好的路径规划算法已成为移动机器人领域的一个热点问题。
2 运行结果
部分代码:
path_value=calculation_path_value(new_population);
[sort1,index]=sort(path_value);
new_population=new_population(index);
path_value=calculation_path_value(new_population);
smooth_value=calculation_smooth_value(new_population);
fit_value=(weight_length./path_value)+(weight_smooth./smooth_value);
mean_path_value=zeros(1,max_generation);
min_path_value=zeros(1,max_generation);
for i=1:max_generation
new_population_1=selection(new_population,fit_value);
new_population_1=crossover(new_population_1,p_crossover);
new_population_1=mutation(new_population_1,p_mutation,G,r);
new_population_1=GenerateSmoothPath(new_population_1,G);
new_population=new_population_1;
path_value=calculation_path_value(new_population);
smooth_value=calculation_smooth_value(new_population);
fit_value=(weight_length./path_value)+(weight_smooth./smooth_value);
mean_path_value(i)=mean(path_value);
[~,ma]=max(fit_value);
min_path_value(i)=path_value(ma);
min_path{i}=new_population(ma);
end
figure(1);
plot(mean_path_value,'r');
hold on;
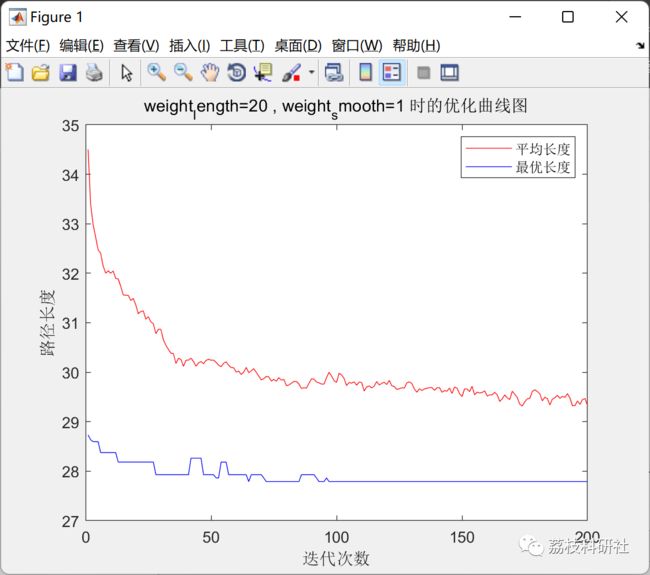
title(['weight_length=',num2str(weight_length),' , weight_smooth=',num2str(weight_smooth),' 时的优化曲线图']);
xlabel('迭代次数');
ylabel('路径长度');
plot(min_path_value,'b');
min(min_path_value)
legend('平均长度','最优长度');
[~,min_index]=min(min_path_value);
minmin_path=min_path{min_index};
minmin_path=minmin_path{1};
figure(2);
hold on;
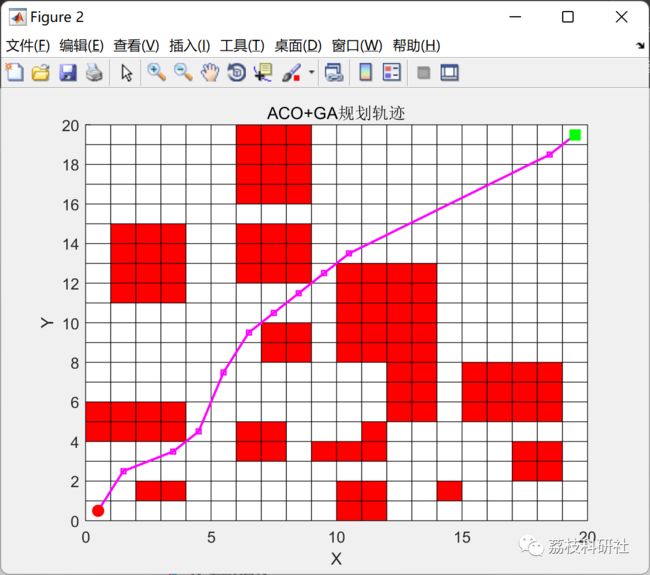
title('ACO+GA规划轨迹');
xlabel('X');
ylabel('Y');
for i=1:r
for j=1:r
if G(i,j)==1
x1=j-1;y1=r-i;
x2=j;y2=r-i;
x3=j;y3=r-i+1;
x4=j-1;y4=r-i+1;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],'r');
hold on
else
x1=j-1;y1=r-i;
x2=j;y2=r-i;
x3=j;y3=r-i+1;
x4=j-1;y4=r-i+1;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);
hold on
end
end
end
hold on
%%%%%%%%%%%%%%%%%%%%%%%%绘制最短路径路线图%%%%%%%%%%%%%%%%%%%%%%%%%%%
LENGTH_minmin_path=length(minmin_path);
RX=minmin_path;
RY=minmin_path;
for i=1:LENGTH_minmin_path
RX(i)=ceil(minmin_path(i)/r)-0.5;
RY(i)=r-mod(minmin_path(i),r)+0.5;
if RY(i)==r+0.5
RY(i)=0.5;
end
end
hold on
plot(RX,RY,'ms-','LineWidth',1.5,'markersize',4);
plot(0.5,0.5,'ro','MarkerSize',4,'LineWidth',4); % 起点
plot(19.5,19.5,'gs','MarkerSize',5,'LineWidth',5); % 终点
toc
3 参考文献
[1]谷星澍. 基于改进PSO-ACO算法的机器人路径规划研究[D].东北石油大学,2020.DOI:10.26995/d.cnki.gdqsc.2020.000123.
[2]许伦辉,曾豫豪.基于改进ACO和三次B样条曲线的路径规划[J].计算机仿真,2022,39(07):407-411.