Bishop 模式识别与机器学习读书笔记_ch2.1 离散型概率分布

ch2.1 常见的离散型概率分布

---

概率论在解决模式识别问题中起着重要作用。本章介绍的分布及性质为后续的复杂模型理解提供了应用基础，也会在简单模型的上下文中讨论一些关键的统计概念，例如贝叶斯推断。

分布的一个重要作用是密度估计，即假设数据点是独立且相同分布的，在给定有限集 $\{{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N\}$ 观测值的情况下，对随机变量 $\mathbf{x}$ 的概率分布 $p(\mathbf{x})$ 进行建模。

存在问题：密度估计问题本质上是病态问题（ill-posed），因为产生有限的观测数据集的概率分布有无限多种。实际上，任何在数据点 ${\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N$ 处概率非零的概率分布 $p(x)$ 都是⼀个潜在的候选。选择⼀个合适的分布与模型选择的问题相关，这是模式识别领域的⼀个中心问题。

分布按照变量类型分为离散型分布和连续型分布，⼆项分布、多项分布、狄利克雷分布均属于离散型分布，高斯分布属于连续分布。这些分布都属于参数分布（parametric distribution），之所以被称为参数分布，是因为少量可调节的参数控制了整个概率分布，需要事先知道密度的类型。另一种密度估计方法是非参数（nonparametric）密度估计方法。这种方法中分布的形式通常依赖于数据集的规模。这些模型仍然具有参数，但是这些参数控制的是模型的复杂度而不是分布的形式。本章最后，我们会考虑三种非参数化方法：直方图、最近邻以及核函数。

1. 二元变量

对于⼀个二元随机变量 $x\in \{0,1\}$. 例如，$x$ 可能描述了扔硬币的结果，$x=1$ 表示“正面”，$x=0$ 表示反面。我们可以假设由⼀个损坏的硬币，这枚硬币正面朝上的概率未必等于反面朝上的概率。$x=1$ 的概率被记作参数 $\mu$，因此
KaTeX parse error: Undefined control sequence: \notag at position 22: …\vert \mu)=\mu \̲n̲o̲t̲a̲g̲ ̲
其中 $0\le \mu \le 1$. 我们可以看到，$p(x=0|\mu )=1-\mu$. 综合这两种情况，$x$ 的概率分布可以写成
KaTeX parse error: Undefined control sequence: \notag at position 38: …x(1-\mu)^{1-x} \̲n̲o̲t̲a̲g̲ ̲
称为伯努利分布（Bernoulli distribution）。

from scipy.stats import bernoulli
import matplotlib.pyplot as plt
import numpy as np

p = 0.3
r = bernoulli.rvs(p, size=100) # 产生1000个随机变量
print('1出现的频率为：',sum(r)/100) # 1出现的总数占比接近 p
plt.stem(r) # 画火柴棒图
plt.show()

1出现的频数为： 28

很容易证明，这个分布是归一化的，并且均值和方差分别为
KaTeX parse error: Undefined control sequence: \notag at position 75: …(1-\mu)+\mu =1 \̲n̲o̲t̲a̲g̲ ̲

$$\mathbb{E}[x]=\sum _{x}x\cdot Bern(x)=1\times Bern(x=1|\mu )+0\times Bern(x=1|\mu )=1\times \mu +0\times (1-\mu )=\mu \text{\hspace{1em}(1)}$$

KaTeX parse error: Undefined control sequence: \notag at position 128: …mes(1-\mu)=\mu \̲n̲o̲t̲a̲g̲ ̲

$$\text{var}[x]=\mathbb{E}[x^2]-\mathbb{E}[x{]}^2=\mu -{\mu }^2=\mu (1-\mu )\text{\hspace{1em}(2)}$$

对于观测数据集 $\mathcal{D}=\{f{x}_1,\cdots ,x_N\}$ 是分布$p(x|\mu )$ 的独立采样，似然函数可写为
$$p(\mathcal{D}|\mu )=\prod _{n=1}^{N}p(x_n|\mu )=\prod _{n=1}^N{\mu }^{x_n}(1-\mu {)}^{1-x_n}\text{\hspace{1em}(3)}$$
在频率学家的观点看来，可以通过最大似然函数来估计 $\mu$ 的值，或者等价地，最大化对数似然函数。在伯努利分布的情形下，对数似然函数为
KaTeX parse error: Undefined control sequence: \notag at position 108: …n)\ln(1-\mu)\} \̲n̲o̲t̲a̲g̲ ̲
在这种观点中，值得注意的⼀点是对数似然函数只通过和式 ${\sum }_n{x}_n$ 依赖于 $x_n$ 的 $N$ 次观察。这个和式是这个分布下数据的充分统计量（sufficient statistic），我们后面将详细研究充分统计量的重要作用。如果我们令 $\ln p(\mathcal{D}|\mu )$ 关于 $\mu$ 的导数等于零，我们就得到了最⼤似然的估计值
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \frac{\partial…
即
$${\mu }_{ML}=\frac{1}{N}\sum _{n=1}^N{x}_n\text{\hspace{1em}(4)}$$
称为样本均值（sample mean）。如果我们把数据集里 $x=1$（正面朝上）的观测的数量
记作 $m$，那么我们可以把公式（4）写成下面的形式
$${\mu }_{ML}=\frac{m}{N}\text{\hspace{1em}(5)}$$

因此在最大似然的框架中，正面朝上的概率是数据集里正面向上的观测所占的比例。

from scipy.stats import bernoulli

p = 0.3 # 参数
mean, var = bernoulli.stats(p, moments='mv')
print('总体均值：{0}; 总体方差为：{1}'.format(mean, var)) # 总体均值为 p;方差为p(1-p)

# 通过观测样本均值来估计总体均值
r = bernoulli.rvs(p, size=10000) # 产生10000个服从贝努力分布的随机变量
print('样本均值为：', sum(r)/10000)

结果为

总体均值：0.3; 总体方差为：0.21
样本均值为： 0.3045

现在假设我们扔⼀个硬币 3 次，碰巧 3 次都是正面朝上。那么 $N=m=3$，且 ${\mu }_{ML}=1$。这种情况下，最大似然的结果会预测所有未来的观测值都是正面向上（因为极大似然只根据观测样本进行总体特征的估计），常识告诉我们这个是不合理的。

注释：事实上，这是最大似然中过拟合现象的⼀个极端例子。我们稍后会看到，通过引⼊ $\mu$ 的先验分布，我们会得到⼀个更合理的结论。

我们也可以求解给定数据集规模 $N$ 的条件下，$x=1$ 的观测出现的数量 $m$ 的概率分布，这种多次贝努力分布称为二项分布（binomial distribution）。根据公式（3）可以看到，这个概率正比于 ${\mu }^m(1-\mu {)}^{N-m}$。为了得到归⼀化系数，我们注意到，在 $N$ 次抛掷中，我们必须把所有获得 $m$个正面朝上的方式都加起来，因此二项分布可以写成
KaTeX parse error: Undefined control sequence: \notag at position 59: …m(1-\mu)^{N-m} \̲n̲o̲t̲a̲g̲ ̲
其中
KaTeX parse error: Undefined control sequence: \notag at position 35: …{N!}{(N-m)!m!} \̲n̲o̲t̲a̲g̲ ̲
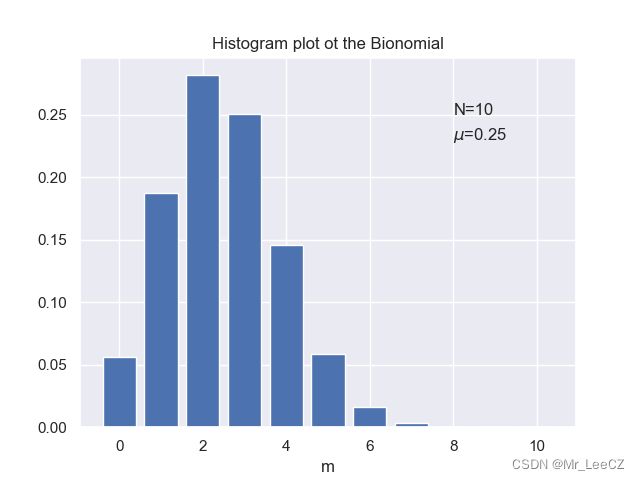
二项分布是从总数为 $N$ 的完全相同的物体中选择 $m$ 个物体的方式的总数。下面给出了 $N=10$ 且 $\mu =0.25$ 情况下的二项分布示意图。

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")

N = 10
mu = 0.25 # 参数

m = np.arange(0,11)
pf = binom.pmf(m, N, mu) # 概率质量函数，x为m的取值
print(pf.sum()) # 和为 1
plt.bar(m,pf)
plt.xlabel('m')

plt.annotate("N={}".format(N), (8, 0.25))
plt.annotate("$\mu$={}".format(mu), (8, 0.23))
plt.title('Histogram plot ot the Bionomial')
plt.show()

由于 $m=x_1+\cdots +x_N$，并且对于每次观察，均值和方差都分别由公式（1）和公式（2）给出，因此我们有
KaTeX parse error: Undefined control sequence: \notag at position 59: …rt N,\mu)=N\mu \̲n̲o̲t̲a̲g̲ ̲

KaTeX parse error: Undefined control sequence: \notag at position 86: …u)=N\mu(1-\mu) \̲n̲o̲t̲a̲g̲ ̲

推导过程：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{E}[m]&…
又因为
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{E}[m^2…
所以
KaTeX parse error: Undefined control sequence: \notag at position 82: …u^2=N\mu(1-\mu)\̲n̲o̲t̲a̲g̲ ̲
二项分布（多次贝努力分布）的编程练习如下：

from scipy.stats import binom
import numpy as np
import matplotlib.pyplot as plt

N = 10
p = 0.25 # 参数

mean,var = binom.stats(N, p, moments='mv')
print('总体均值为：{0}；总体方差为：{1}'.format(mean,var))

输出结果

总体均值为：2.5；总体方差为：1.875

**注释：**总体均值为 $N\ast p=10\ast 0.25=2.5$，总体方差为 $N\ast p\ast (1-p)=10\ast 0.25\ast 0.75=1.875$

2. Beta 分布

问题：根据公式（5），我们已经看到伯努利分布的参数 $\mu$ 的极大似然解，因此在二项分布中，这个极大似然解在小规模的数据集会给出严重的过拟合结果。

策略：从贝叶斯的观点看待这个问题，我们需要引入⼀个关于 $\mu$ 的先验概率分布 $p(\mu )$. 为了找到这个先验分布，我们注意到似然函数（3）是某个因子与 ${\mu }^x(1-\mu {)}^{1-x}$ 的乘积的形式。如果我们选择⼀个正比于 $\mu$ 和 $(1-\mu )$ 的幂指数的先验概率分布，那么后验概率分布（正比于先验和似然函数的乘积）就会有着与先验分布相同的函数形式，这个性质被叫做共轭性（conjugacy）。因此，我们把先验分布选择为Beta分布（二项分布的共轭分布），定义为
$$\text{Beta}(\mu |a,b)=\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}{\mu }^{a-1}(1-\mu {)}^{b-1}\text{\hspace{1em}(6)}$$
其中，$\Gamma (\cdot )$ 为 Gamma 函数，$a$ 和 $b$ 是控制先验概率的参数，因为它是控制参数 $\mu$ 的参数，称为超参数。

from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")

x = np.linspace(0, 1, 100)
for i, [a, b] in enumerate([[0.1, 0.1], [1, 1], [2, 3], [8, 4]]):
    plt.subplot(2, 2, i + 1)
    plt.xlim(0, 1)
    plt.ylim(-0.1, 3)
    plt.plot(x, beta.pdf(x,a,b))
    plt.xlabel('$\mu$')
    plt.annotate("a={}".format(a), (0.1, 2.5))
    plt.annotate("b={}".format(b), (0.1, 2.1))
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wZkBjcrf-1666341374237)(Img/Beta.png)]

公式（6）的因子部分保证了分布在 $[0,1]$ 上的积分为 1，即
KaTeX parse error: Undefined control sequence: \notag at position 44: …t a,b)d\mu = 1 \̲n̲o̲t̲a̲g̲ ̲
Beta 分布的期望和方差分别为
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{E}[\mu…

KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{E}[\mu…

KaTeX parse error: Undefined control sequence: \notag at position 128: …a+b)^2(a+b+1)} \̲n̲o̲t̲a̲g̲ ̲

由于 Beta 分布是二项分布的共轭分布，可作为先验分布，利用贝叶斯公式，获得参数 $\mu$ 的后验分布

KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ p(\mu\vert \ma…

又因为结果的系数不影响极值点，所以，后验估计可以记作

KaTeX parse error: Undefined control sequence: \notag at position 93: …ert m+a,N-m+b) \̲n̲o̲t̲a̲g̲ ̲

例子： 利用二项分布的似然估计和其共轭先验分布 Beta 分布获取参数 $\mu$ 的后验分布

• 二项分布

关于变量 $m$ 的二项分布（已知参数 $\mu$ 的情况）可视化
KaTeX parse error: Undefined control sequence: \notag at position 59: …m(1-\mu)^{N-m} \̲n̲o̲t̲a̲g̲ ̲
其中 $N=m=1$，$\mu =0.5$

from scipy.stats import binom
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")

N = 1
mu = 0.5 # 参数

m = np.arange(0,2)
pf = binom.pmf(m, N, mu) # 概率质量函数，x为m的取值
print(pf.sum()) # 和为 1
plt.bar(m,pf,width=0.2)
plt.xlabel('m')

plt.annotate("N={}".format(N), (0.6, 0.3))
plt.annotate("$\mu$={}".format(mu), (0.6, 0.25))
plt.title('Histogram plot ot the Bionomial')
plt.show()

• 关于变量 $\mu$ 的二项分布（参数 $\mu$ 未知待估计）可视化

KaTeX parse error: Undefined control sequence: \notag at position 59: …m(1-\mu)^{N-m} \̲n̲o̲t̲a̲g̲ ̲

其中，$N=m=1$，$\mu$ 未知

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")

N = 1
mu = np.linspace(0,1,100) # 参数

y = mu # 概率质量函数，x为m的取值

plt.plot(mu,y)
plt.xlim(0,1)
plt.ylim(0,2)
plt.xlabel('$\mu$')
plt.annotate("N = m = {}".format(N), (0.2, 1.5))
#plt.annotate("$\mu$={}".format(mu), (0.6, 0.25))
plt.title('Histogram plot ot the Bionomial')
plt.show()

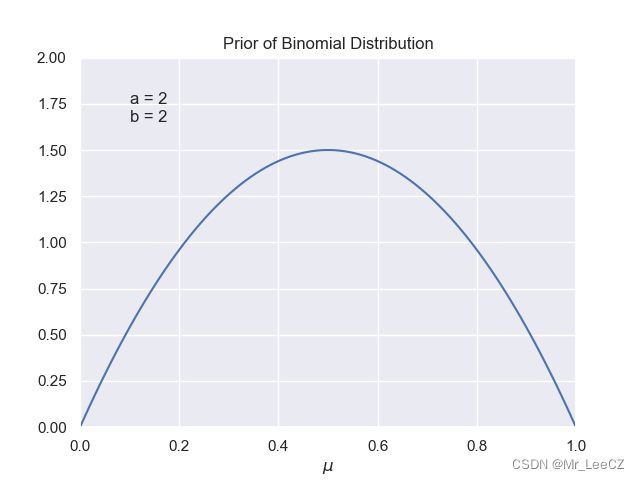
• 二项分布的共轭先验分布

Beta 分布的可视化
$$\text{Beta}(\mu |a,b)=\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}{\mu }^{a-1}(1-\mu {)}^{b-1}\text{\hspace{1em}(7)}$$
其中，$a=2$，$b=2$

from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")

mu = np.linspace(0, 1, 100)
a = 2
b = 2

plt.xlim(0, 1)
plt.ylim(-0, 2)
plt.plot(mu, beta.pdf(mu,a,b))
plt.xlabel('$\mu$')
plt.annotate("a = {}".format(a), (0.1, 1.75))
plt.annotate("b = {}".format(b), (0.1, 1.65))
plt.title('Prior of Binomial Distribution')
plt.show()

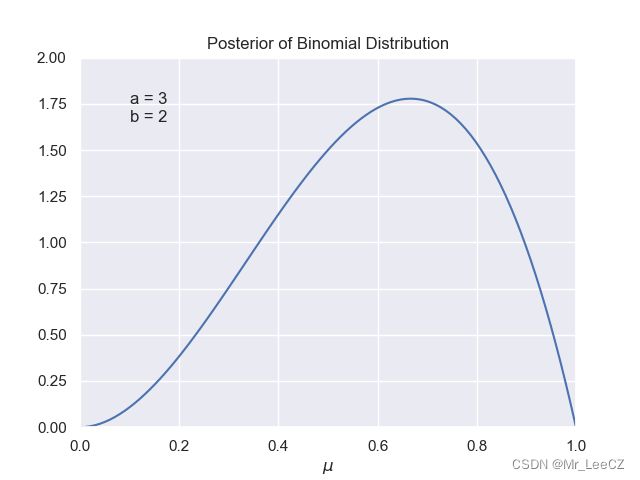
• 后验分布

后验分布的可视化
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ p(\mu\vert m,l…
由于在该例子中，$N=m=1$, 和（7）相比，即 Beta 分布的参数 $a$ 增加了 1，参数 $b$ 未改变。

from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")

mu = np.linspace(0, 1, 100)
a = 3
b = 2

plt.xlim(0, 1)
plt.ylim(-0, 2)
plt.plot(mu, beta.pdf(mu,a,b))
plt.xlabel('$\mu$')
plt.annotate("a = {}".format(a), (0.1, 1.75))
plt.annotate("b = {}".format(b), (0.1, 1.65))
plt.title('Posterior of Binomial Distribution')
plt.show()

**注释：**由于参数 $\mu$ 的分布不是一个值，因此估计 参数 $\mu$ 最合适的值是其众数，通常是分布的极值点。

5. 处理流数据的序贯法

在数据独立同分布的场景下，**序贯法（sequential approach)**是非常有效的，即每次只处理一个数据然后丢弃的方法。其最大的优势是节约内存，非常适合处理海量数据的处理，而且极大似然方法可以方便的应用于此方法。

在序贯法的框架下，需要利用下一次试验预测结果，即在给定的数据集 $\mathcal{D}$ 预测 $x$ 的分布。根据概率的和积规则 $p(x,\mu )=p(\mu )p(x|\mu )$ 可知
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ p(x=1\vert\mu)…
可知，下一次试验的预测结果是给定数据集分布的参数 $\mu$ 的期望。由公式（5）和（8）可得
$$p(x=1|\mu )=\frac{m+a}{m+a+l+b}\text{\hspace{1em}(9)}$$
当 $m,l\to \infty$，公式（9）将退化为极大似然解（5）.

6. 多项式分布

待续

可知
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ p(x=1\vert\mu)…
可知，下一次试验的预测结果是给定数据集分布的参数 $\mu$ 的期望。由公式（5）和（8）可得
$$p(x=1|\mu )=\frac{m+a}{m+a+l+b}\text{\hspace{1em}(9)}$$
当 $m,l\to \infty$，公式（9）将退化为极大似然解（5）.

6. 多项式分布

待续