机器学习--一元线性回归06

回归分析(regression analysis)用来建立方程模拟两个或者多个变量之间如何关联
被预测的变量叫做：因变量(dependent> variable), 输出(output)
被用来进行预测的变量叫做： 自变量(independent variable), 输入(input)
一元线性回归包含一个自变量和一个因变量 两个变量的关系用一条直线来模拟

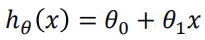
这个方程对应的图像是一条直线，称作回归线。其中，1为回归线的斜率， 0为回归线的截距。

真实结果与我们预测的结果之间是不是存在一定的误差呢，是的。既然存在这个误差，那我们就将这个误差给衡量出来，损失函数。

线性回归的损失和优化

损失函数

如何去减少这个损失，使我们预测的更加准确些？既然存在了这个损失，我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实是数学当中的求导功能）回归的总损失！！！
如何去求模型当中的W，使得损失最小？（目的是找到最小损失对应的W值）

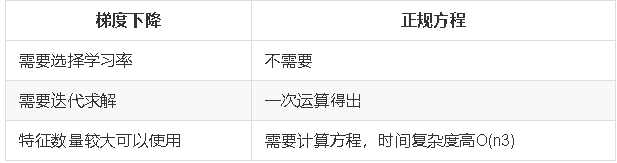
线性回归经常使用的两种优化算法

• 正规方程
• 梯度下降法

什么是正规方程

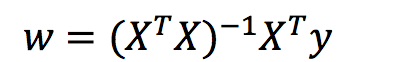
理解：X为特征值矩阵，y为目标值矩阵。直接求到最好的结果

缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

正规方程求解举例，以下表示数据：

即
运用正规方程方法求解参数：

正规方程的推导，把该损失函数转换成矩阵写法：

其中y是真实值矩阵，X是特征值矩阵，w是权重矩阵

对其求解关于w的最小值，起止y,X 均已知二次函数直接求导，导数为零的位置，即为最小值。

求导：
注：式(1)到式(2)推导过程中, X是一个m行n列的矩阵，并不能保证其有逆矩阵，但是右乘XT把其变成一个方阵，保证其有逆矩阵。

式（5）到式（6）推导过程中，和上类似。

什么梯度下降

梯度下降计算公式

梯度下降计算一元线性回归方程

导入包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

载入数据

data = pd.read_csv("data.csv", delimiter=",", header=None)
x_data = data.iloc[:,0]
y_data = data.iloc[:,1]
plt.scatter(x_data,y_data)
plt.show()

设置超参数

# 学习率learning rate
lr = 0.0001
# 截距
b = 0 
# 斜率
k = 0 
# 最大迭代次数
epochs = 50

损失函数计算，最小二乘法

def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
    return totalError / float(len(x_data)) / 2.0

梯度下降优化损失函数

def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        b_grad = 0
        k_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
            k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
        # 更新b和k
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)
        # 每迭代5次，输出一次图像
#         if i % 5==0:
#             print("epochs:",i)
#             plt.plot(x_data, y_data, 'b')
#             plt.plot(x_data, k*x_data + b, 'r')
#             plt.show()
    return b, k

训练过程

print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data + b, 'r')
plt.show()

sklearn-一元线性回归

导入包

from sklearn.linear_model import LinearRegression
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

载入数据

data = pd.read_csv("data.csv", delimiter=",", header=None)
x_data = data.iloc[:,0]
y_data = data.iloc[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)

(100,)
创建并拟合模型

x_data = x_data[:,np.newaxis]
y_data = y_data[:,np.newaxis]
print(x_data.shape)
print(y_data.shape)

(100, 1)
(100, 1)

estimator = LinearRegression()
estimator.fit(x_data, y_data)

画图

plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, estimator.predict(x_data), 'r')
plt.show()