机器学习—一元线性回归
hypothesis
问题引入:有一个北京市房屋面积与售价的数据集,使用这组数据集训练算法,然后通过算法预测一个给定房屋面积的房子的售价。
思考流程:使用训练集训练算法,算法会根据训练集内各变量的关系拟合一条hypothesis(或者叫回归方程)。hypothesis曲线描述的是被解释变量(房价)的预测值与解释变量(房屋面积)之间的关系。
hypothesis假设为:H(x)=θ0+ θ1x。
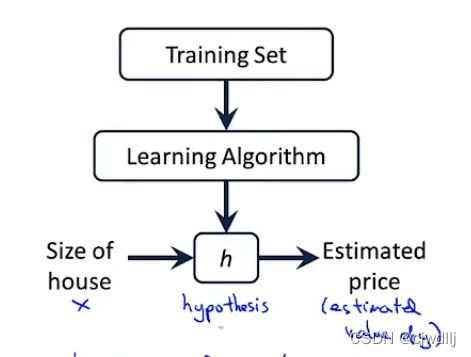
要注意的是数据之间的拟合方式不只有一种,也就是说hypothesis并不是唯一的,可以改变参数θ的取值,得到不同的hypothesis。
那么问题来了:如何判断最优的hypothesis呢?这就要引入代价函数的概念。
代价函数
对于给定的hypothesis:H(x)=θ0+ θ1x,对于训练集的第i个样本(x(i),y(i)),都会有唯一确定的被解释变量的拟合值hθ(x(i)),即hθ(x(i))=θ0+ θ1x(i)。hypothesis设定越精确,则被解释变量的预测值hθ(x(i))与真实值y(i)之间的距离(差的平方)越小。对于所有的样本而言,最优的hypothesis就是使得差的平方和最小。这是一种常见的优化方法,即统计学上的最小二乘法。
基于残差平方和思想可以构造解决一元线性回归问题最常见的代价函数,即下图中的Cost Function。代价函数的最小值就对应着最佳的hypothesis拟合。
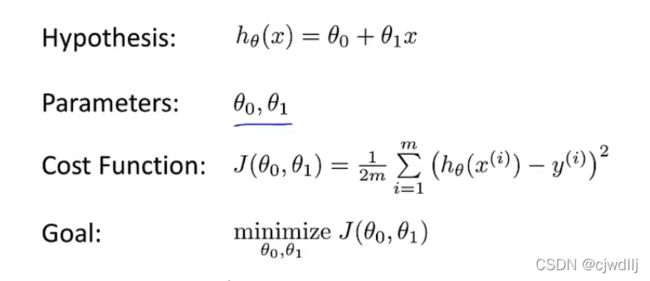
hypothesis与代价函数之间存在着一一对应的关系。给定参数θ0和θ1的值,对应一条确定的hypothesis与代价函数的给定值;改变θ0和θ1的值,hypothesis的形式与代价函数的值也会对应的发生改变。那么通过寻找一个特定的θ0和θ1,使得代价函数的取值最小,此时hypothesis就是最优的拟合。
如何寻找代价函数的最小值,这里介绍一种算法——梯度下降算法。
梯度下降
1. 梯度下降算法
梯度下降算法的作用:梯度下降算法可以获取一个任意函数的局部最小值。
梯度下降算法的思想:假设求函数J(θ0,θ1)的最小值,先设定θ0和θ1的初始值(通常情况下可以设定θ0=0,θ1=1),然后一点点改变θ0和θ1的取值使得J(θ0,θ1)的值下降,重复上述过程,直到找到J(θ0,θ1)的最小值。
梯度下降算法的直观显示:一组给定的θ0,θ1初始值,就对应着下图中的一个初始点,从该初始点出发,会对应着一条最优的下降路径,沿着该路径获取J(θ0,θ1)的一个局部最小值。当改变0,θ1的初始值,就又会对应着另一个初始点,从这个初始点出发又会到达J(θ0,θ1)的另一个局部最小值。因此梯度下降算法得出的是一个函数的局部最小值。
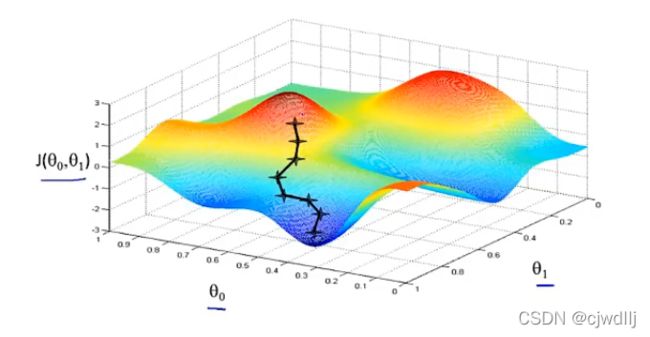
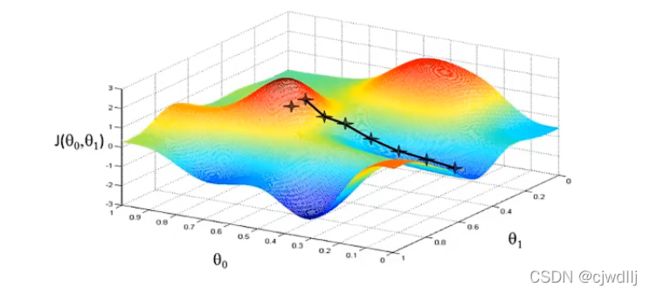
梯度下降算法的公式如下图所示:

符号含义:
(1):= 赋值
(2)α是learning rate。α主要影响参数改变的大小,如果α过小,会导致算法需要迭代多次才能找到函数的最小值;如果α过大,可能会导致参数取值跨过最小值点,导致无法收敛或发散。
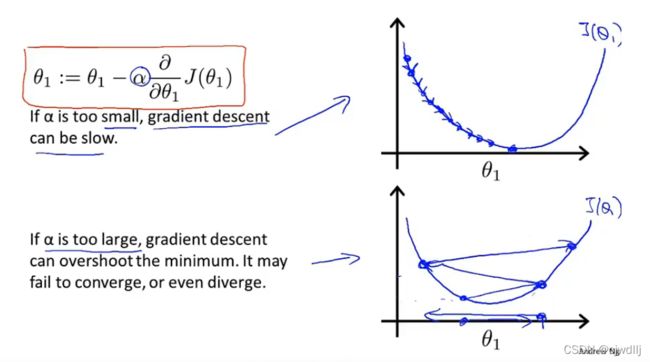
貌似α的取值会对算法产生影响,但其实不必太过担忧这一点。因为即使当α的值是固定的,也可以通过偏导项的调节找到函数的最小值。
(3)αJ(θ0,θ1)/αθj是偏导项。
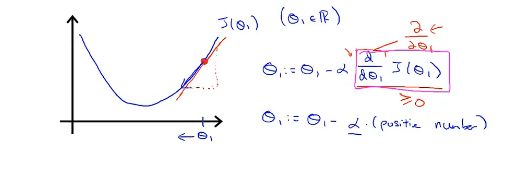
我们可以借助一元函数导数的概念来理解这一项的作用。假设0=0,J(θ0,θ1)=J(θ1)。
一个点的导数就是过这一点的切线的斜率。在下图中的红点处,切线的斜率为正,因此导数项的取值为正,而α的总为正,代入梯度下降的公式,可得θ1是在变小的,也就是朝着函数最小值点的方向更新。当初始点位于最小值点的左侧时,可以发现θ1的更新方向也是我们所希望的那样。
那么,当初始化点恰好位于函数的最小值点处,参数θ1的值会如何更新呢?因为在函数的最小值点处导数值为0,代入梯度下降的工公式中可以发现,θ1的取值是不变的。也就是说,当初始值就是函数的最小值点时,梯度下降算法什么都没有做,这也是我们所期望的。
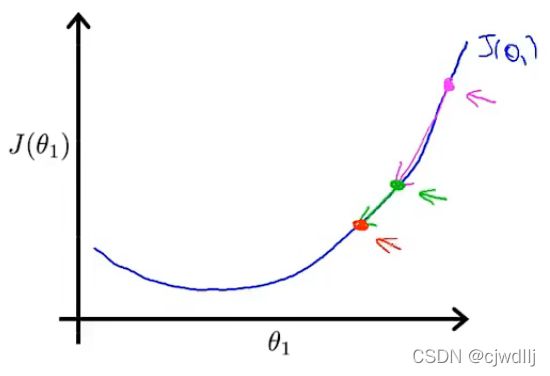
刚刚说到,即使α的值固定,梯度下降也能凭借导数项的调节寻找到函数的最小值,这是为什么呢?在下图中的粉色点,导数值在三个点中是最大的。对应着该点θ1的移动是最大的;随着粉色点向着绿点和红点移动,导数值在不断变小,对应的θ1的移动也越小。因此,由于导数的自动调节,即使α的取值固定,在越接近函数的最小值点的时候,θ1的移动幅度越小,因此不用太过担心在接近函数最小值点时由于α值偏大导致参数θ跨过最小值点。
(4)同步更新
梯度下降中θ的更新方式是同步更新,见下图T形中左侧的部分。右侧部分参数的更新方式是错误的。这两个公式的主要区别是,右侧公式是先更新θ0的值,然后用更新后的θ0代入梯度下降算法公式中更新了θ1的值;而左侧公式是用更新前的θ0和θ1的值代入梯度下降算法公式,计算出θ0和θ1更新后的值。

虽然右侧的更新方式可能也会得出正确的计算结果,但是当我们提到梯度下降算法,指的就是同步更新。
2. 线性回归算法
将梯度下降算法应用于一元线性回归的代价函数中,便可以求解最优的hypothesis。

因为线性回归的代价函数是凸函数(如下图所示),不存在局部最小值,因此使用梯度下降算法求解的代价函数的最小值就是全局最小值。
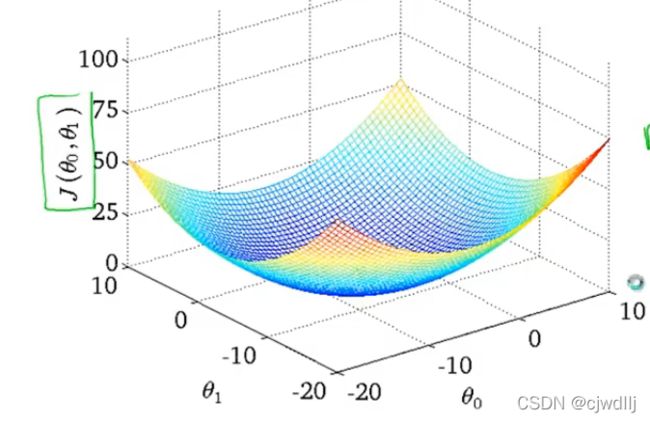
解线性回归问题的梯度下降算法又叫“Batch梯度下降”,batch的中文意思是批。这里之所以这么叫是因为线性回归的梯度下降算法使用全样本。