基于划分的聚类分析——K-means（机器学习）

目录

一、实验内容

二、实验过程

1、算法思想

2、算法原理

3、算法分析

三、源程序代码

四、运行结果及分析

五、实验总结 

---

一、实验内容

---

1. 熟知聚类分析的概念、分类方法，理解良好聚类分析的特征。
2. 掌握聚类分析的度量指标；
3. 掌握基于划分的聚类方法的基本概念；
4. 利用k-means算法，实现基于划分的聚类分析。

二、实验过程

---

1、算法思想

---

        聚类分析是一种典型的无监督学习，用于对未知类别的样本进行划分，将它们按照一定的规则分成若干个分簇，把相似（距离相近）的样本聚在一个类簇中，把不相似的样本分为不同类簇，从而揭示样本之间内在的性质以及相互之间的联系规律。

2、算法原理

---

        K-means聚类算法，是一种广泛使用的聚类算法，其中k是需要指定的参数，即需要创建的簇的数目，K-means算法中的k个簇的质心可以通过随机的方式获得，但是这些点需要位于数据范围内。在算法中，计算每个点到质心得距离，选择距离最小的质心对应的簇作为该数据点的划分，然后再基于该分配过程后更新簇的质心。重复上述过程，直至各个簇的质心不再变化为止。

3、算法分析

---

（1）（随机）选择K个聚类的初始中心。

（2）依次遍历每一个样本点，求其到K个聚类中心的距离，将样本点归类到距离最小的中心的聚类，如此迭代n次。

（3）每次迭代过程中，利用均值等方法更新各个聚类的中心点(质心)。

（4）对K个聚类中心，利用2,3步迭代更新后，如果位置点变化很小(可以设置阈值)，则认为达到稳定状态，迭代结束，对不同的聚类块和聚类中心可选择不同的颜色标注。

三、源程序代码

---

import matplotlib.pyplot as plt
import numpy as np
#1、先列出一列数组
y=np.array([[2,3],[2,2],[3,4],[1,2],[9,8],[8,8],[8,7],[9,9],[1,5],[2,4],[7.9,7],[8.9,9],[2,1],[7,9],[9,7],[8,8],[9,7],[8,8.5]])
#2，方便画图
x_scatter=[data[0] for data in y]
y_scatter=[data[1] for data in y]
#3，分类 0类，1类
k=[0,1]
#3，先给出两个点
y_center=np.array([[7,7],[9,9]],dtype=np.float64)
y_center_new=np.copy(y_center)
#4，用于判断是否退出
flag = True
#5，用于后者分类
y_res=np.zeros(len(y))
#6，用于判断是否退出
tmp=0
 
while flag and tmp<10:
    tmp+=1
    for i in range(len(y)):                 # y里面的点数
        item=y[i]                           # 二维数组里面的一维数组
        d0=(item[0]-y_center[0][0])**2+(item[1]-y_center[0][1])**2
        print("d0 is ",d0)
        d1=(item[0]-y_center[1][0])**2+(item[1]-y_center[1][1])**2
        print("d1 is ",d1)
        y_res[i]=0 if d0>d1 else 1          # 测距分类
 
    y_res_like_0=[[i,i] for i in y_res]     # 二维列表，里面非0即1
    temp_center=y*y_res_like_0              # 乘0得0，乘1得1            ####关键，到后面中心点不会动的原因是，y中分类已经分的固定了，每次计算用都是固定的几个数
    y_center_new[0]=np.sum(temp_center,axis=0)/np.sum(y_res)   # x坐标求和，y坐标求和，以及得到的y_res(1的求和)
 
    y_res_like_1=[[1-i,1-i] for i in y_res]       # 二维列表，里面非0即1
    temp_center=y*y_res_like_1              # 乘0得0，乘1得1            ####关键，到后面中心点不会动的原因是，y中分类已经分的固定了，每次计算用都是固定的几个数
    y_center_new[1]=np.sum(temp_center,axis=0)/(len(y_res)-np.sum(y_res)) #y_res的总数减去1的总数等于0的总数
 
 
    if(y_center !=y_center_new).any():    # 判断前后两次中心点是否相同
        y_center = y_center_new
    else:
        flag = False                     # 相同直接退出
 
#7画图
    plt.scatter(x_scatter,y_scatter,c='blue',marker='.')
    plt.scatter([y_center[0][0],y_center[1][0]],[y_center[0][1],y_center[1][1]],c="red",s=100,marker='*')
    plt.title("K-means")
    plt.show()

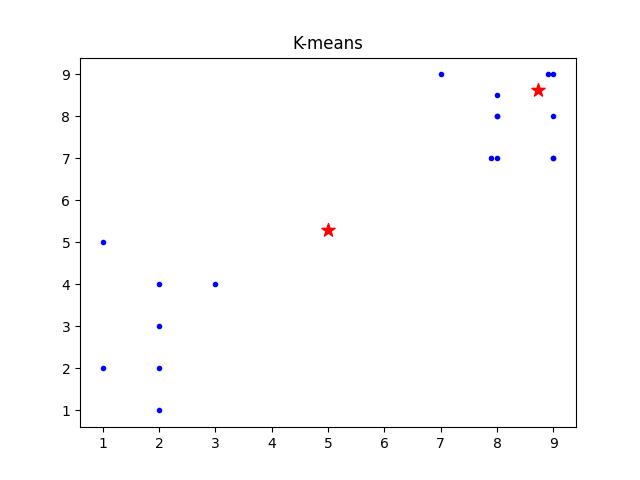
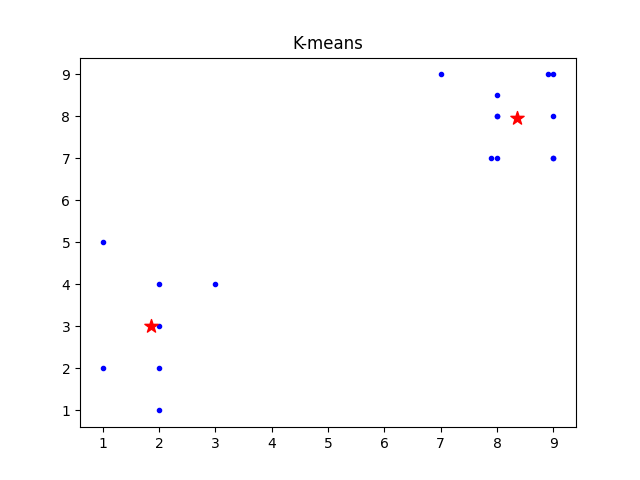
四、运行结果及分析

---

 

五、实验总结 

---

        聚类分析的度量指标用于对聚类结果进行评判，分为内部指标和外部指标两大类。外部指标指用事先指定的聚类模型作为参考来评判聚类结果的好坏；内部指标是指不借助任何外部参考，只用参与聚类的样本评判聚类结果的好坏。

        聚类的目标是得到较高的簇内相似度和较低的簇间相似度，使得簇间的距离尽可能大，簇内样本与簇中心的距离尽可能小。